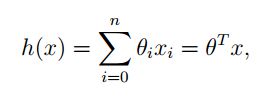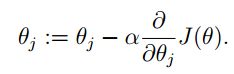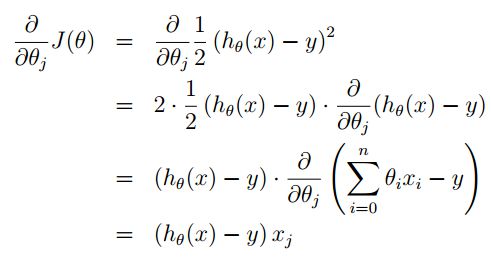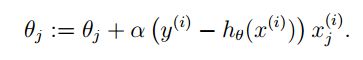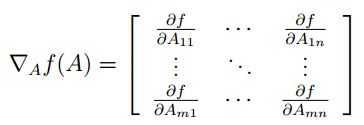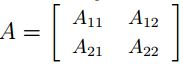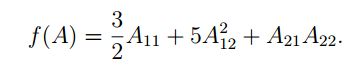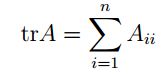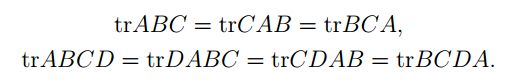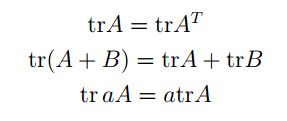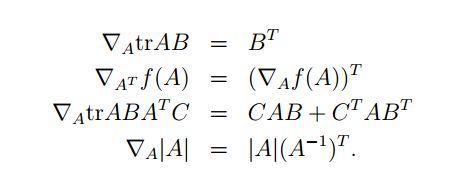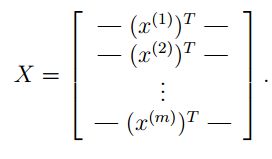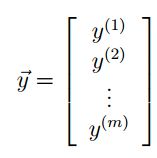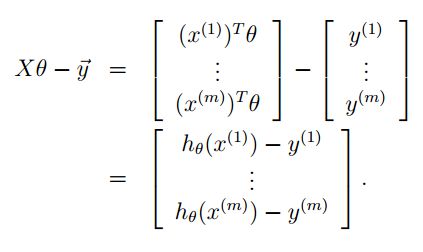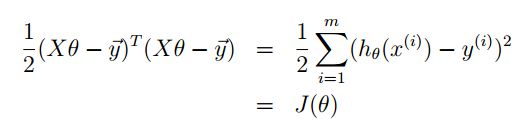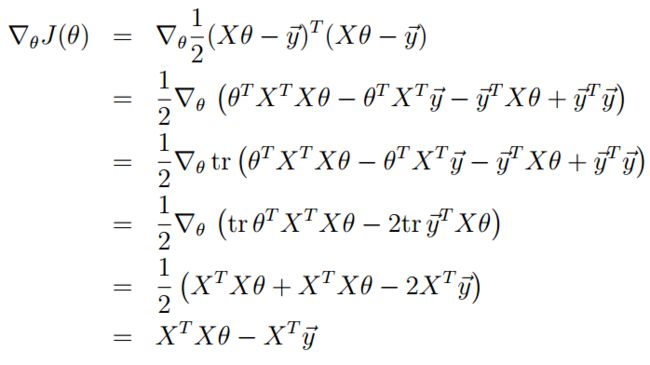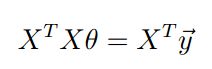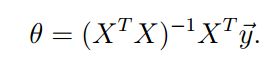监督学习之梯度下降——Andrew Ng机器学习笔记(一)
写在前面的话
一直对机器学习非常感兴趣,现在终于脚踏式的开始了。自己感觉很开心,而且也是看着Andrew Ng老师的视频自学。想用博客记录下自己学习机器学习的点滴。
Andrew Ng老师,中文名:吴恩达(1976-),华裔美国人,是斯坦福大学计算机科学系和电子工程系副教授,人工智能实验室主任。吴恩达是人工智能和机器学习领域国际上最权威的学者之一。吴恩达也是在线教育平台Coursera的联合创始人(with Daphne Koller)。现在是百度人工智能实验室的首席科学家。
Andrew Ng机器学习的分类
Andrew Ng老师的这套视频是斯坦福的公开课,在网易公开课上可以找到。Andrew Ng老师的机器学习分类主要有4类:
- 监督学习(Supervised Learning)
- 学习理论(Learning Theory)
- 无监督学习(Unsupervised Learning)
- 强化学习(Reinforcement Learning)
梯度下降
梯度下降是基于迭代的算法,但正规方程(normal equations)可以一步求解最优解。什么是正规方程可以在博客的正规方程这个小标题中看到,当然你也可以去百度等等。
问题
这是我最喜欢的一种授课方式,发现问题,然后讲述怎么去解决问题,同时引出相应的理论。
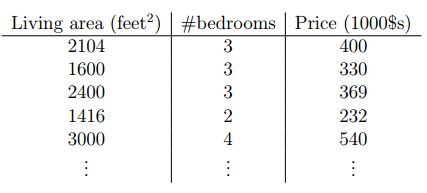
Andrew Ng老师举得例子是房子关于价格的例子,即给出一组房屋价格与卧室数量,房屋面积的对应关系。如下图:
我们要完成的任务是:给定一个房屋的面积和卧室的数量预测出他的价格。
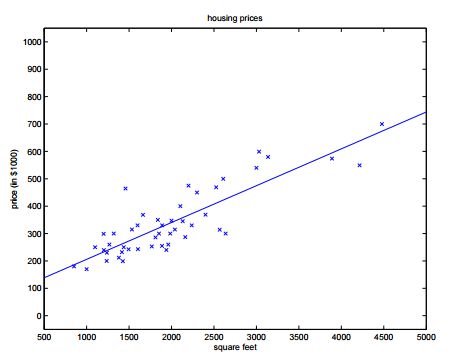
我们的解决方案是,根据已知的数据进行拟合。这就是监督学习,所谓的监督就是先前有一组正确数据作为训练,经过这组数据训练之后就可以进行房屋价格的预测了。我们先简化问题,只给出房屋面积与价格的对应的关系,把这组数据绘制到二维坐标系中,便可以看到很多散点。比如像这样:
我们通过这组点可以的到一个形如 y=a+bx 这样的方程。其中 a,b 都是参数,只要给定一个 x 就可以得到一个 y 。由于这个方程是线性的,所以称之为线性回归。当问题进一步复杂的时候(有更多对 y 的影响因子,即有更多的 x ),我们遵循传统的命名方式就可以得到如下形式的方程:
其中式子的最后是向量的乘法,展开就和前面的相等了。
得到了这个式子,但是我们的评价他的好坏。思想就是计算这个式子在给定 x 的情况下,计算的值与真实与这个 x 对应的函数值做差然后平方。将所有的已知数据都进行相同的操作。然后求和。这样我们就可以得到一个评价函数,然后利用评价函数值比较两个 h(x) 函数的好坏了。
我们换个思想,把 h 看成 θ 的函数。然后使得评价函数值最下,就可以求出 h 函数中的 θ 。给出的评价函数的样子如下:
其中的 1/2 完全是为了计算的方便,在后面你就会看到。
下面的我们的主要任务就是去找一组 θ ,使得 J(θ) 的值最下。这类问题称之为无约束最优化问题。梯度下降法就是其中的一种方法。
我们求解的问题中有多个 θ ,即目标函数 J(θ) 是关于 θ 的多元函数。与之相关的有一个称之为梯度的概念(你可以在高等数据的课本中找到),他说的意识是函数沿着梯度方向的函数值增长最快。我们现在要使得目标函数最下,即就是要找最快的下降方向。那么负梯度方向就是下降最快的方向。梯度的求法就是对目标函数的所有因变量求偏导。
梯度下降法的核心思想就是,给定一个初始点,在该点处求其梯度,迭代得到下一个 θ 点。直到梯度为零时结束。
为什么是梯度为零时结束
当迭代点是最优时,其对应的梯度为零称之为无约束问题解得一阶必要条件
证明的核心思想是利用最优点处利用泰勒展开,因为已经是最优点,所以在其附近的点函数值近似相等,便可以得到梯度为零的结论
详细证明参见 李董辉 数值最优化算法与理论(第二版)19页
可以得到 θ 的迭代式子为:
其中的 α 称之为步长,在最优化课中我们有好几种方法来确定这个 α 的值,Andrew Ng在课上说他们是在试验中手动选取的,这里我们先不用去纠结他,我们可以选他为一。对于 J(θ) 的偏导过程如下:
在这里你就看到,我们在构造 J(θ) 时1/2的出现就是为了与指数的在求导时抵消。
经过简单的替换之后我们就可以得到 θ 新的迭代公式:
进而根据我们之前说的思想得到算法的描述如下:
另一种解决方案:正规方程
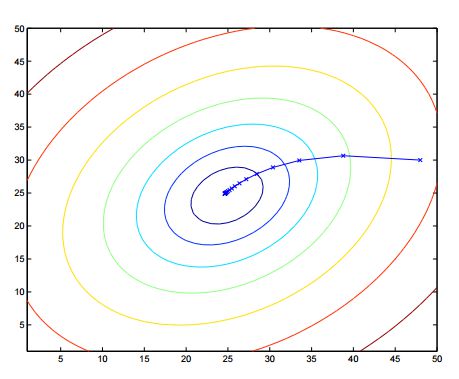
如下图圆圈表示函数的等值线,在算法收敛到最优点时收敛速度太慢,或者由于步长选择不当,使得我们在最优值附近摇摆。
关于矩阵的一些预备知识
函数 f 是从 m∗n 的矩阵到实数域的映射,对其求梯度可以表示为如下形式:
矩阵的迹为矩阵的对角元素之和。表示形式如下:
Andrew Ng还在课上将了一些迹的性质(我也没有证明,只是验证了一下)
还有一些关于梯度的性质:
这些性质我没有证明,但是可以验证是正确的。
正规方程(normal equations)
求正规方程的思想是将所有数据写到矩阵中通过矩阵的运算一步得到最优的解。首先将所有的自变量数据都写到一个矩阵中,比如前面问题中的房屋面积大小,卧室的个数等等。形式如下:
其中 x 是一个列向量,它的上标表示第几组数据,将 x 转置之后就成了行向量,这样所有的数据就构成了一个矩阵 X 。
再将所有因变量写在一起构成列向量,比如前面问题中的房屋价格。形式如下:
前面说过的线性方程模型就可以写成如下形式:
然后在利用前面矩阵 X 和向量 y ,可以进行如下的构造:
我们知道:
其中 z 为列向量。利用同样的道理,我们就可以得到 J(θ) 的矩阵表达形式:
做如下推导:
这个推导过程不是很好理解,我自己做了如下推导:
由无约束问题解得一阶必要条件,可以得到 J(θ) 对 θ 求梯度结果为零。则可以得到:
这个式子称为正规方程(normal equations)。
从而可以得到 J(θ) 的最优值为:
可以看出利用前面构造的矩阵一步就可以求出来。但是这里需要求 XTX 的逆,这不并不总是很容易。
参考文献
[1] 李董辉 数值最优化算法与理论(第二版)科学出版社
[2] Andrew Ng 斯坦福公开课
end