【深度学习】传统RNN的正向传播与反向传播

循环神经网络的正向传播与反向传播

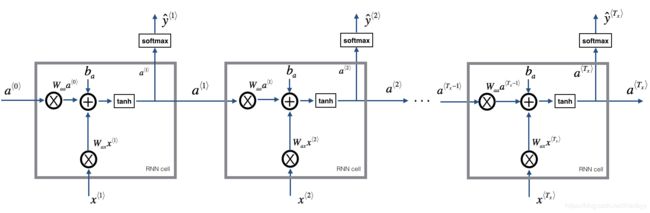
一、正向传播

前向循环计算公式：
$$a^{(t)}=tanh(W_{ax}{x}^{(t)}+W_{aa}{a}^{(t-1)}+b_a)$$
$$y^{(t)}=softmax(W_{ya}{a}^{(t)}+b_y)$$

python实现rnn前向传播算法

# parameters是参数Waa、Wax、Wya、by、b等组成的字典
# a_prev是上一时间步的输出（a）
# x是训练数据
def rnn_step_forward(parameters, a_prev, x):
    
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
    a_next = np.tanh(np.dot(Wax, x) + np.dot(Waa, a_prev) + b) # hidden state
    p_t = softmax(np.dot(Wya, a_next) + by) # unnormalized log probabilities for next chars # probabilities for next chars 
    
    return a_next, p_t
def rnn_forward(X, Y, a0, parameters, vocab_size = 27):
    
    # Initialize x, a and y_hat as empty dictionaries
    x, a, y_hat = {}, {}, {}
    
    a[-1] = np.copy(a0)
    
    # initialize your loss to 0
    loss = 0
    
    for t in range(len(X)):
        
        # Set x[t] to be the one-hot vector representation of the t'th character in X.
        # if X[t] == None, we just have x[t]=0. This is used to set the input for the first timestep to the zero vector. 
        x[t] = np.zeros((vocab_size,1)) 
        if (X[t] != None):
            x[t][X[t]] = 1
        
        # Run one step forward of the RNN
        a[t], y_hat[t] = rnn_step_forward(parameters, a[t-1], x[t])
        if t==0:
            print(y_hat[t].shape)
        
        # Update the loss by substracting the cross-entropy term of this time-step from it.
        loss -= np.log(y_hat[t][Y[t],0])
        
    cache = (y_hat, a, x)
        
    return loss, cache

二、反向传播

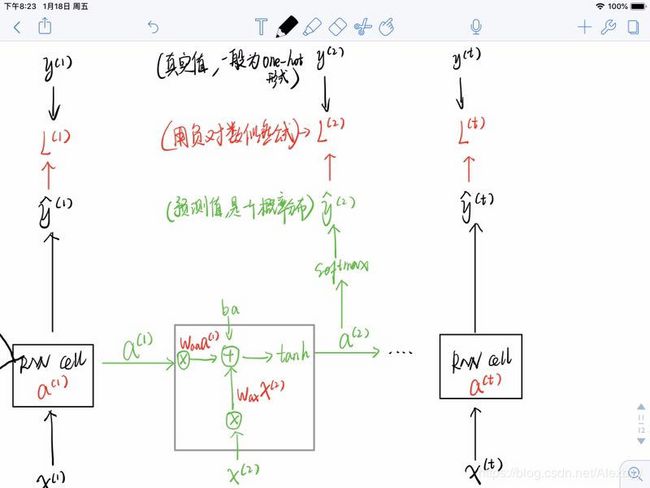
1. 上图中的$L^t$是每一步计算出来的损失（用负对数似然公式），最终的总损失$L=\sum (L^t)$

• 负对数似然
  神经网络的输出通常是概率分布，一般使用负对数似然来作为损失函数。例如：假设训练集Y的one-hot表示是（0,1,0）,预测值y的分布为(0,1,0.6, 0.3),则对于该训练样本的损失loss=-log0.6，然后最小化该loss，目的是让预测值y与真实y相对应位置的概率尽量大。
  如果X表示所有的输入，Y表示我们观测到的目标$${\theta }_{ML}=ar{g}_{\theta }maxP(Y|X;\theta )$$
  假设样本是独立同分布的，则上面公式实际情况是一连串训练样本的预测概率相乘，这种情况下可以用对数函数进行等价转换（方便计算）：$${\theta }_{ML}=ar{g}_{\theta }max\sum _{i=1}^{m}logP(y^{(i)}|x^{(i)};\theta )$$
  对于循环神经网络，其损失函数是每一时间步损失的和，也就是上图中所有的L之和：$$L(x^{(1)},...,x^{(t)},y^{(1)},...,y^{(t)})=\sum _t{L}^{(t)}=-\sum _{t}log{P}_{model}(y^{(t)}|x^{(1)},...,x^{(t)})$$
  其中 $P_{model}(y^{(t)}|x^{(1)},...,x^{(t)})$ 需要读取模型输出向量y与真实向量y对应的项。

2. RNN的反向传播需要按时间步从后往前推导（本质是一个优化问题和链式求导），我们要优化的目标函数就是总损失$L=\sum (L^t)$（最小化它），然后从t到0对其逐步求导。

例如求时间步t处，L对参数$W_{ay}$的偏导数：

3. RNN某一时间步内反向传播计算公式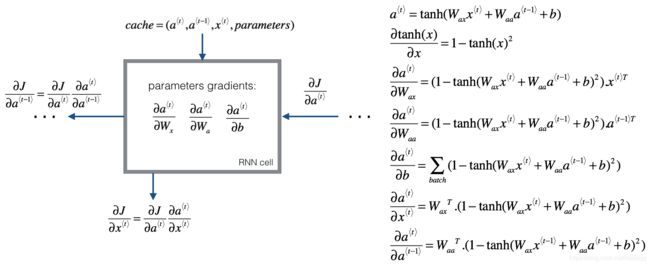

python实现RNN反向传播算法

def rnn_step_backward(dy, gradients, parameters, x, a, a_prev):
    
    gradients['dWya'] += np.dot(dy, a.T)
    gradients['dby'] += dy
    da = np.dot(parameters['Wya'].T, dy) + gradients['da_next'] # backprop into h
    daraw = (1 - a * a) * da # backprop through tanh nonlinearity
    gradients['db'] += daraw
    gradients['dWax'] += np.dot(daraw, x.T)
    gradients['dWaa'] += np.dot(daraw, a_prev.T)
    gradients['da_next'] = np.dot(parameters['Waa'].T, daraw)
    return gradients

 """ Returns: parameters -- python dictionary containing: X -- 训练数据 Y -- 真实值 parameters -- dict，include：Waa，Wax，Wya，by，b cache--每一步的预测值y、a及训练样本x组成的字典 """
def rnn_backward(X, Y, parameters, cache):
    # Initialize gradients as an empty dictionary
    gradients = {}
    
    # Retrieve from cache and parameters
    (y_hat, a, x) = cache
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
    
    # each one should be initialized to zeros of the same dimension as its corresponding parameter
    gradients['dWax'], gradients['dWaa'], gradients['dWya'] = np.zeros_like(Wax), np.zeros_like(Waa), np.zeros_like(Wya)
    gradients['db'], gradients['dby'] = np.zeros_like(b), np.zeros_like(by)
    gradients['da_next'] = np.zeros_like(a[0])
    
    # Backpropagate through time
    for t in reversed(range(len(X))):
        dy = np.copy(y_hat[t])
        dy[Y[t]] -= 1
        gradients = rnn_step_backward(dy, gradients, parameters, x[t], a[t], a[t-1])
    
    return gradients, a