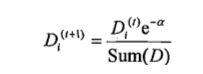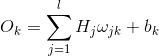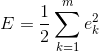期末作业——基于机器学习算法的LOL比赛预测(求高分,拜托拜托)
前言:2018年5月2日,各大高校男生宿舍不约而同的爆发出尖叫和呼喊声。难道是“单身少年们”集体受到刺激,而引发的集体抗议吗?在这一切的背后究竟隐藏着怎样的秘密?
其实真相是:
一、题目背景
近年来,随着科技的不断进步和人们传统思想的不断改变,电子竞技正在飞速发展。刚刚,亚奥理事会公布了亚运电子体育表演赛的六个项目:《英雄联盟》、《实况足球》、《炉石传说》、《星际争霸2》、《Arena of Valor》(王者荣耀国际版)和《皇室战争》。它们将作为电子竞技携手奥运的排头兵,出现在八月举行的雅加达亚运会赛场上。而我本人对英雄联盟(LOL)这门赛事比较感兴趣,于是自选了这个题目。
二、样本来源
本人选用的样本数据来源于英雄联盟官网 http://lpl.qq.com/es/lpl/2018/
三、数据可视化及数据预处理
在我们拿到原始数据后,需要对数据进行预处理,提高数据质量,从而提高挖掘结果的质量。通过刚才的网页数据我们可以发现,其官方网站上所给出的信息非常多。但实际上我们在预测的过程中并不需要那么多的数据。
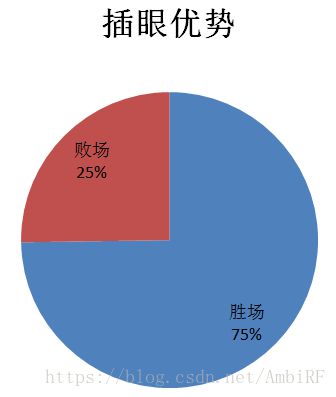
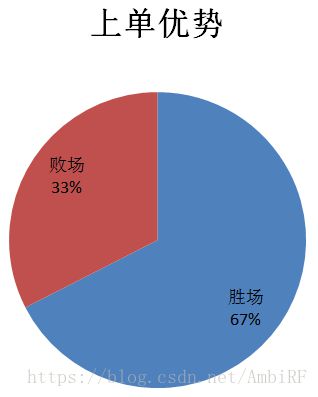
通过做出数据可视化,来观察其特征对最后结果的影响:
由此看见,无论是插眼还是上单对于最后结果的影响都举足轻重,后边的数据可视化我就不一一展示了。当然,除了运用这种直观的方式观察和比对特征值对于最后结果的影响之外,我还采用了经验法(其实就是问大神)。这种方法的好处就是除了提供的特征外,我们还可以自己发掘一些隐藏关系,建立新的特征并验算新的特征值对于结果的影响。
最后我选取了队伍十个特征,作为预测的基础。他们分别是:上单差距、中单差距、打野差距、下路差距、协作能力差距、平均小龙数差距、平均大龙数差距、场均插眼差距、场均击杀差距和场均死亡差距。
首先对特征做一个简单的介绍,前四条差距代表了战队出战选手个人能力的差距,我们都知道一个选手的好坏无疑影响着最后的结果,尾大不掉的现象是确确实实存在的。除此之外,协作能力的差距这一个特征并没有体现在官方所提供的数据中,因此我自己拟定了一个函数:
这代表着击杀对方一名选手所需要的己方人手。而场均大龙小龙则代表着队伍对于地图公共资源的争夺意识,场均插眼差距可以反映队伍对于地图信息量的把握,只有时时刻刻掌握敌方动向,才能知己知彼,百战不殆。
将我们所需要的数据收集后,按照所选定的十个特征值整理成表格的形式,保存,作为数据库。
四、算法选择
4.1使用Adaboost算法预测
4.1.1 boost前提介绍
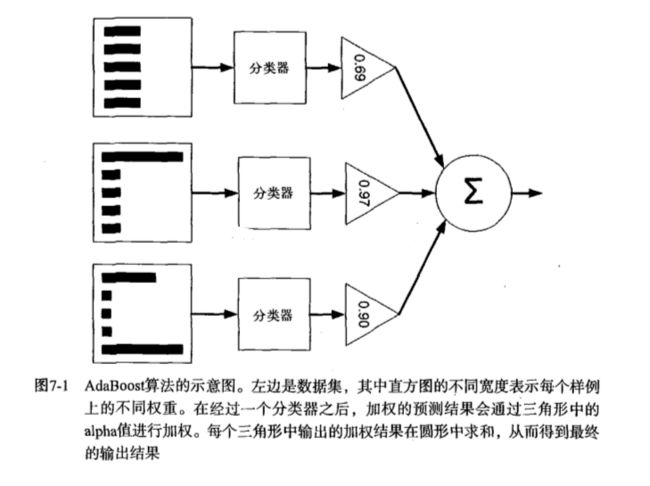
提升(Boost)简单地来说,提升就是指每一步我都产生一个弱预测模型,然后加权累加到总模型中,然后每一步弱预测模型生成的的依据都是损失函数的负梯度方向,这样若干步以后就可以达到逼近损失函数局部最小值的目标。boosting分类的结果是基于所有分类器的加权求和结果的,分类器每个权重代表的是其对应分类器在上一轮迭代中的成功度。而bagging中的分类器权重是相等的。其中Adaboost就是boosting方法中一个极具代表性的分类器。
4.1.2 Adaboost训练算法介绍
AdaBoost(adaptiveboosting):训练数据中的每个样本,并赋予其一个权重,这些权重构成了向量D。一开始,这些权重都初始化成相等值。首先在训练数据上训练出一个弱分类器并计算该分类器的错误率,然后在同一数据集上再次训练弱分类器。重新调整每个样本的权重,第一次分对的样本的权重将会降低,分错的样本的权重将会提高。AdaBoost为每个分类器都分配了一个权重值alpha,其基于每个弱分类器的错误率进行计算的。错误率的定义:
AdaBoost算法的流程图:
对权重向量D更新,如果某个样本被正确分类,那么该样本的权重改为:
计算出D后,AdaBoost继续迭代重复训练调整权重,直到训练错误率为0或者弱分类器的数据达到用户指定值为止。
4.1.3 完整AdaBoost算法实现
伪代码
对每次迭代: 利用buildStump()函数找到最佳的单层决策树 将最佳单层决策树加入到单层决策树数组 计算alpha 计算新的权重向量D 更新累计类别估计值 如果错误率等于0.0,则退出循环
函数大致包括以下几个:
1、基于单层决策树的Adaboost训练过程
2、Adaboost分类函数
如果我们需要在一个较为复杂的数据集中使用adaboost,最好还加上一个自适应数据加载函数。(注:代码均在本文结尾处统一放置)
4.1.4 实际应用
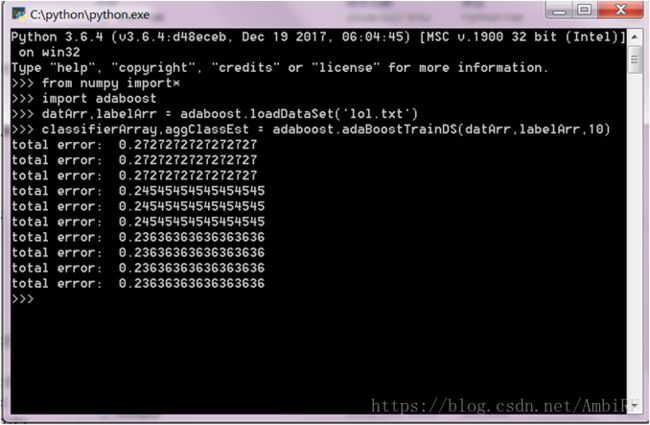
在这里需要注意的是AdaBoost 需要确保标签类别是+1和-1而非1和0,且自适应数据加载函数假定最后一个特征是类别标签,所以在这里可以通过修改数据的txt文档或者是修改自适应数据加载函数来使得程序正常运行。(注:书中默认程序所限制所有数据应均为浮点数,所以在导入任何数据库的时候都应转换成浮点数)结果:
ROC曲线:
由最终结果可以看出,对于结果的预测可以达到75%的正确率,所以使用adaboost算法是一个比较合适的选择。
4.2 运用BP神经网络模型
4.2.1 模型简介
BP(Back Propagation)神经网络是一种具有三层或者三层以上的多层神经网络,每一层都由若干个神经元组成,它的左、右各层之间各个神经元实现全连接,即左层的每一个神经元与右层的每个神经元都由连接,而上下各神经元之间无连接。BP神经网络按有导师学习方式进行训练,当一对学习模式提供给神经网络后,其神经元的激活值将从输入层经各隐含层向输出层传播,在输出层的各神经元输出对应于输入模式的网络响应。然后,按减少希望输出与实际输出误差的原则,从输出层经各隐含层,最后回到输入层(从右到左)逐层修正各连接权。由于这种修正过程是从输出到输入逐层进行的,所以称它为“误差逆传播算法”。随着这种误差逆传播训练的不断修正,网络对输入模式响应的正确率也将不断提高。
4.2.2 神经网络的概念
BP神经网络是一种多层的前馈神经网络,其主要的特点是:信号是前向传播的,而误差是反向传播的。具体来说,对于如下的只含一个隐层的神经网络模型:
BP神经网络的过程主要分为两个阶段,第一阶段是信号的前向传播,从输入层经过隐含层,最后到达输出层;第二阶段是误差的反向传播,从输出层到隐含层,最后到输入层,依次调节隐含层到输出层的权重和偏置,输入层到隐含层的权重和偏置。
4.2.3神经网络的流程
再判断算法是否已经收敛,常见的有指定迭代的代数,判断相邻的两次误差之间的差别是否小于指定的值等等。
4.2.4 程序实现
因为我对python运用还不算十分熟悉,在运用神经网络的时候,我使用的是MATLAB程序,运行结果如下:
可以看出虽然拟合的结果不错,但仍然有些比较大的偏差,为此,我又在此基础上尝试了两外一种神经网络的拟合。
4.3 广义回归神经网络
4.3.1 基本简介
GRNN神经网络 广义回归神经网络(GRNN)是Donald FSpecht在1991年提出的。GRNN是一种正则化的径向基网络,通常用来实现函数逼近。广义回归神经网络是建立在数理统计基础上的径向基函数网络,其理论基础是非线性回归分析。广义回归神经网络对x的回归定义不同于径向基函数的对高斯权值的最小二乘法叠加,他是利用密度函数来预测输出。特点:训练速度快,非线性映射能力强。
4.3.2 算法流程
GRNN 在结构上由四层构成,分别为输入层、模式层、 求和层和输出层。
1.输入层为向量,维度为m,样本个数为n,线性函数为传输函数。
2.隐藏层与输入层全连接,层内无连接,隐藏层神经元个数与样本个数相等,也就是n,传输函数为径向基函数。
3.加和层中有两个节点,第一个节点为每个隐含层节点的输出和,第二个节点为预期的结果与每个隐含层节点的加权和。
4.输出层输出是第二个节点除以第一个节点。
4.3.3 模型实践
从最后的结果可以看出相比于BP神经网络而言,广义回归网络更适合这个数据集。
五、总结及心得
这是我真正意义上第一次选择一个从未有过的数据集进行预测,从最开始原始数据的查找和分析,到数据可视化和特征值的选择,对我来说都是不小的考验。在今年进行学习的《机器学习》这门课程中我学到最多的并不是与机器学习相关的内容,而是接受了一种全新的自学模式。我想这种学习模式对于我们的求知欲和创造性的激发是正常上课所给与不了的,也和国外的教学模式不谋而合。这个学期我曾经无数次的为了弄明白一个程序段所包含的意义不眠不休,但是最后看到预测结果的合理的时候让我局的一切的辛苦都是值得的。在今后的学习中,我可能会出国读研转换学习方向重点学习人工智能这一专业,有了这一学期的入门和铺垫,我会更加快速地适应这门科学。最后,我要感谢老师和助教不厌其烦给我帮助和解答,感谢!
参考资料:
CSDN——Adaboost 2.24号:ROC曲线的绘制和AUC计算函数
CSDN——AdaBoost--从原理到实现
中国邮电出版社——《机器学习实战》
CSDN——神经网络学习笔记(六) 广义回归神经网络 https://blog.csdn.net/cyhbrilliant/article/details/52694943CSDN——【通俗讲解】BP神经网络 https://blog.csdn.net/guomutian911/article/details/78635617
from numpy import *
import matplotlib.pyplot as plt
def loadSimpData():
datMat = matrix([[ 1. , 2.1],
[ 2. , 1.1],
[ 1.3, 1. ],
[ 1. , 1. ],
[ 2. , 1. ]])
classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
return datMat,classLabels
def loadDataSet(fileName): #general function to parse tab -delimited floats
numFeat = len(open(fileName).readline().split('\t')) #get number of fields
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr =[]
curLine = line.strip().split('\t')
for i in range(numFeat-1):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data
retArray = ones((shape(dataMatrix)[0],1))
if threshIneq == 'lt':
retArray[dataMatrix[:,dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:,dimen] > threshVal] = -1.0
return retArray
def buildStump(dataArr,classLabels,D):
dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
m,n = shape(dataMatrix)
numSteps = 10.0; bestStump = {}; bestClasEst = mat(zeros((m,1)))
minError = inf #init error sum, to +infinity
for i in range(n):#loop over all dimensions
rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();
stepSize = (rangeMax-rangeMin)/numSteps
for j in range(-1,int(numSteps)+1):#loop over all range in current dimension
for inequal in ['lt', 'gt']: #go over less than and greater than
threshVal = (rangeMin + float(j) * stepSize)
predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#call stump classify with i, j, lessThan
errArr = mat(ones((m,1)))
errArr[predictedVals == labelMat] = 0
weightedError = D.T*errArr #calc total error multiplied by D
#print "split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError)
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump,minError,bestClasEst
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((m,1))/m) #init D to all equal
aggClassEst = mat(zeros((m,1)))
for i in range(numIt):
bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump
alpha = float(0.5*log((1.0-error)/max(error,1e-16)))#calc alpha, throw in max(error,eps) to account for error=0
bestStump['alpha'] = alpha
weakClassArr.append(bestStump) #store Stump Params in Array
expon = multiply(-1*alpha*mat(classLabels).T,classEst) #exponent for D calc, getting messy
D = multiply(D,exp(expon)) #Calc New D for next iteration
D = D/D.sum()
#calc training error of all classifiers, if this is 0 quit for loop early (use break)
aggClassEst += alpha*classEst
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1)))
errorRate = aggErrors.sum()/m
print ("total error: ",errorRate)
if errorRate == 0.0: break
return weakClassArr,aggClassEst
def adaClassify(datToClass,classifierArr):
dataMatrix = mat(datToClass)#do stuff similar to last aggClassEst in adaBoostTrainDS
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m,1)))
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\
classifierArr[i]['thresh'],\
classifierArr[i]['ineq'])#call stump classify
aggClassEst += classifierArr[i]['alpha']*classEst
print (aggClassEst)
return sign(aggClassEst)
def plotROC(predStrengths, classLabels):
import matplotlib.pyplot as plt
cur = (1.0,1.0) #cursor
ySum = 0.0 #variable to calculate AUC
numPosClas = sum(array(classLabels)==1.0)
yStep = 1/float(numPosClas); xStep = 1/float(len(classLabels)-numPosClas)
sortedIndicies = predStrengths.argsort()#get sorted index, it's reverse
fig = plt.figure()
fig.clf()
ax = plt.subplot(111)
#loop through all the values, drawing a line segment at each point
for index in sortedIndicies.tolist()[0]:
if classLabels[index] == 1.0:
delX = 0; delY = yStep;
else:
delX = xStep; delY = 0;
ySum += cur[1]
#draw line from cur to (cur[0]-delX,cur[1]-delY)
ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b')
cur = (cur[0]-delX,cur[1]-delY)
ax.plot([0,1],[0,1],'b--')
plt.xlabel('FALSE Positiverate'); plt.ylabel('TRUE Positive rate')
plt.title('ROC curve for WINE')
ax.axis([0,1,0,1])
plt.show()
print ("the Area Under the Curve is: ",ySum*xStep)