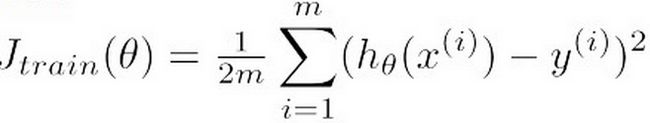系统学习机器学习之模型诊断与调试

实际上，这个问题，或多或少，在之前的总结中，有所涉及，在学习了那么多的理论之后，此篇作为一个2015年的技术提升总结。毕竟，在实战中，理论只能作为方向指导。

实在不高兴自己去写（虽然，完整的自己梳理一遍，对自己的提升帮助很大），这里有篇专业总结：

原文引自：http://blog.sina.com.cn/s/blog_818f5fde0102vx09.html

问题：当我们训练出数据后，发现模型有太大误差，怎么办？

1）鉴别是过拟合还是欠拟合的问题

当发现训练出来的模型误差太大的时候，首先考虑的就应该是是否存在过拟合或者欠拟合的问题。但是，如何对二者进行有效鉴别呢？最简单的方法就是分别计算cross validation error(Jcv) 跟training error(Jtrain)：当Jcv跟Jtrain差不多且Jtrain较大时，当前模型更可能存在欠拟合；当Jcv远远大于Jtrain且Jtrain较小时，当前模型更可能存在过拟合。

我们将整个数据集按照一定比例分为训练集和交叉验证集，假设训练集量为m，交叉验证集量为mcv。首先，我们利用m条训练集训练模型参数，并得到Jtrain；然后，将训练出的模型应用于交叉验证集，得到Jcv。这里附上Jcv和Jtrain的计算方法：

a）Jtrain的计算方法：​

b）Jcv的计算方法：

当然，我们可以对数据集进行多次划分，看看Jcv和Jtrain是否在统计上满足同一大小规律，确认我们的判断结果。

值得提醒的是，很多时候，我们在发现模型结果不理想时，并没有静下心来认真思考究竟是过拟合还是欠拟合，而是胡乱试用各种方法，缺乏针对性，导致调优过程花费了大量的时间。另外，在判断过拟合和欠拟合上有很多其它看似更完美、更理论的方式，但是我觉得没有太大的必要，简单地计算Jcv和Jtrain通常已经能准确定位问题了，性价比显然最高。

 

————————————————分割线————————————————

 

2）如果存在欠拟合，怎么办？

我相信，大多数时候，一开始，我们的算法会是欠拟合的。所以，如果你发现你的算法欠拟合后，恭喜你，你的调优工作才刚刚开始，也就是说，你的模型还差得远呢。正是因为如此，每次我的模型出现过拟合后，我都会开心一阵子，说明问题不大了。

解决欠拟合问题有以下几种方法。

a）添加其他特征

一直以来觉有有句话说得很有道理：“在机器学习里，特征决定了准确率的上限，而算法决定了结果趋近于上限的程度”。这句话也可以翻译成：“巧妇难为无米之炊”。特征是米，每个不同的机器学习算法就是做饭的巧妇。很多人在公司（特别是大公司）待一段时间后，不免都会有一点点失望。因为他们发现，公司里的很多“机器学习/数据挖掘工程师”或者“算法工程师”每天的工作，不过都是在不停地发现和调研新的特征来添加进原有的算法框架里，以提升算法的准确率，而不是发明一些更牛逼、高大上的算法来替换掉原有的算法框架。当然，研究高大上的算法的人有，但并不是那么多。我这里只是想说明特征很重要，而且，调研新的更有效的特征是机器学习里永无止境的有效工作。

不同的应用环境有不同的特征，下面是做搜索排序可能用到的一些特征类别，并不全，只是举个例子提供思路参考。​

在这里，特别说明一下，“组合”、“泛化”、“相关性”三类特征是特征添加的重要手段，无论在什么场景，都可以照葫芦画瓢，总会得到意想不到的效果。除上面的特征之外，“上下文特征”、“平台特征”等等，都可以作为特征添加的首选项。

b）添加多项式特征

这句话的意思其实就是提高模型的复杂度，增加模型的表达空间。例如，将原来的线性模型，通过特征添加，变为二次或三次模型。当然，这里并不需要改变本身的训练算法，只需要在原有的特征空间里添加相应的高次项特征即可。例如，原来有个特征x，可以将x^2或者x^3作为一个新的特征放到原来的线性系统里进行训练。

c）减小正则化参数

正则化的目的就是防止模型过拟合，现在模型出现了欠拟合，当然可以通过减小正则化参数的方法来避免欠拟合，不需要多解释。

 

————————————————分割线————————————————

 

3）如果存在过拟合，怎么办？

学术界关于过拟合的研究很多，这是因为这个主题会更理论一些，看起来更有技术含量一些。

解决过拟合问题有一下几种方法：

a）训练集选用更多样本

虽然我不同意“对于机器学习，样本数量越大训练出来的分类器正确率越高”这句话，但是如果样本量不足是肯定会有问题的。举个极端的例子，如果我们只有三个训练样本，很容易得到一个训练误差为0的模型，但是实际误差却很大，也就是过拟合问题。所以，选择更多的样本有可能在一定程度上解决过拟合的问题。但是，这种方法不一定每次都会奏效。首先，更多的样本并不一定那么容易得到，很多时候样本的获得是需要很大成本的；其次，即使能够得到，也得考虑时间、空间复杂度的问题，我们的算法平台是否允许这么大的样本量；最后，即使前面两个条件都允许，也不一定增加训练样本就能提高模型准确率，这也是为什么一开始我说我不同意“对于机器学习，样本数量越大训练出来的分类器正确率越高”这句话的原因。一开始，随着样本量的增加，模型准确率肯定会相应增加，但是，当样本量达到一定程度（饱和）后，样本量的增加是没有意义的，这个时候就需要用其他方法实现准确率的提升。

b）采用更小的特征集

不仅特征的次数彰显了模型的复杂度，特征集的维数也一样彰显了模型的复杂度。所以，采用更小的特征集，可以解决过拟合的问题。一般，减小特征集的方法有：特征选择和特征抽取。二者的区别是：特征选择是指在原有的特征中选择一部分特征来用，抛弃不重要的特征，新的特征集是原特征集的子集。详细的特征选择方法介绍可以参考这里：http://www.cnblogs.com/heaad/archive/2011/01/02/1924088.html；特征抽取是指通过原有的高维特征构建新的特征，新的特征维度远远低于原有特征的维度，新的每一维特征都是原有所有特征的加权组合。最常见的特征抽取方法有主成分分析（PCA）和因子分析。

c）增大正则化参数

正则化的目的就是防止模型过拟合，这里不解释。

d）减小模型复杂度，降低模型阶次（不推荐）