系统学习深度学习（五） --递归神经网络原理，实现及应用

          递归神经网络（ RNN），是两种人工神经网络的总称，一种是 时间递归神经网络（recurrent neural network），另一种是 结构递归神经网络（recursive neural network）。现在大多数人把recurrent neural network称作循环神经网络，一般RNNs都指循环神经网络，也就是recurrent neural network。时间递归神经网络的神经元间连接构成有向图。，而结构递归神经网络利用相似的神经网络结构递归构造更为复杂的深度网络（大多数为无向图）。两者训练的算法不同，但属于同一算法变体。如之前的Hopfield神经网络就是结构上递归构成。还有BAM,cohen-Grossberg神经网络等。从这里很明显可以看出，时间递归帮助弥补短记忆网络的长记忆扩展（输入是时间相关的序列），而结构递归只是在神经网络结构上的设计（与输入无关），但时间递归神经网络应该是结构递归网络的一个有效改进发展。也就是说，在神经网络年代，提出的神经网络递归结构，被用在了时间序列的递归上，而充分发展出时间递归神经网络，即循环神经网络RNNs,以及后期的LSTM。

      但是大神们说，标准的RNN在实际使用中效果不是很好，真正起到作用的是LSTM，因此RNN只做简单学习，不上源码（转载了两篇，第一个是简单推导，第二个是应用介绍）。

下面是简单推导，转自：http://blog.csdn.net/aws3217150/article/details/50768453

在此之前，我们已经学习了前馈网络的两种结构——多层感知器和卷积神经网络，这两种结构有一个特点，就是假设输入是一个独立的没有上下文联系的单位，比如输入是一张图片，网络识别是狗还是猫。但是对于一些有明显的上下文特征的序列化输入，比如预测视频中下一帧的播放内容，那么很明显这样的输出必须依赖以前的输入， 也就是说网络必须拥有一定的”记忆能力”。为了赋予网络这样的记忆力，一种特殊结构的神经网络——递归神经网络(Recurrent Neural Network)便应运而生了。网上对于RNN的介绍多不胜数，这篇《Recurrent Neural Networks Tutorial》对于RNN的介绍非常直观，里面手把手地带领读者利用Python实现一个RNN语言模型，强烈推荐。为了不重复作者 Denny Britz的劳动，本篇将简要介绍RNN，并强调RNN训练的过程与多层感知器的训练差异不大(至少比CNN简单)，希望能给读者一定的信心——只要你理解了多层感知器，理解RNN便不是事儿:-)。

RNN的基本结构

首先有请读者看看我们的递归神经网络的容貌：

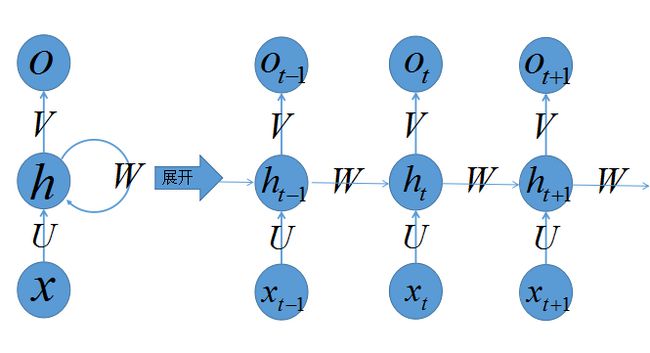
乍一看，好复杂的大家伙，没事，老样子，看我如何慢慢将其拆解，正所谓见招拆招，我们来各个击破。
上图左侧是递归神经网络的原始结构，如果先抛弃中间那个令人生畏的闭环，那其实就是简单”输入层=>隐藏层=>输出层”的三层结构，我们在多层感知器的介绍中已经非常熟悉，然而多了一个非常陌生的闭环，也就是说输入到隐藏层之后，隐藏层还会给自己也来一发，环环相扣，晕乱复杂。
我们知道，一旦有了环，就会陷入“先有蛋还是先有鸡”的逻辑困境，为了跳出困境我们必须人为定义一个起始点，按照一定的时间序列规定好计算顺序，做到有条不紊，于是实际上我们会将这样带环的结构展开成一个序列网络，也就是上图右侧被“unfold”之后的结构。先别急着能理解RNN，我们来点轻松的，先介绍这样的序列化网络结构包含的参数记号：

• 网络某一时刻的输入 xt ，和之前介绍的多层感知器的输入一样， xt 是一个 n 维向量，不同的是递归网络的输入将是一整个序列，也就是 x=[x0,...,xt−1,xt,xt+1,...xT] ，对于语言模型，每一个 xt 将代表一个词向量，一整个序列就代表一句话。
• ht 代表时刻 t 的隐藏状态
• ot 代表时刻 t 的输出
• 输入层到隐藏层直接的权重由 U 表示，它将我们的原始输入进行抽象作为隐藏层的输入
• 隐藏层到隐藏层的权重 W ，它是网络的记忆控制者，负责调度记忆。
• 隐藏层到输出层的权重 V ，从隐藏层学习到的表示将通过它再一次抽象，并作为最终输出。

RNN的Forward阶段

上一小节我们简单了解了网络的结构，并介绍了其中一些记号，是时候介绍它具体的运作过程了。首先在 t=0 的时刻， U,V,W 都被随机初始化好， h0 通常初始化为0，然后进行如下计算：

s1=Ux1+Wh0h1=f(s1)o1=g(Vh1)

这样时间就向前推进，此时的状态 h1 作为时刻0的记忆状态将参与下一次的预测活动，也就是

s2=Ux2+Wh1h2=f(s2)o2=g(Vh2)

，以此类推

st=Uxt+Wht−1ht=f(Uxt+Wht−1)ot=g(Vht)

其中 f 可以是 tanh,relu,logistic 任君选择， g 通常是 softmax 也可以是其他，也是随君所欲。
值得注意的是，我们说递归神经网络拥有记忆能力，而这种能力就是通过 W 将以往的输入状态进行总结，而作为下次输入的辅助。可以这样理解隐藏状态：

h=f(现有的输入+过去记忆总结)

RNN的Backward阶段

上一小节我们说到了RNN如何做序列化预测，也就是如何一步步预测出 o0,o1,....ot−1,ot,ot+1..... ，接下来我们来了解网络的知识 U,V,W 是如何炼成的。
其实没有多大新意，我们还是利用在之前讲解多层感知器和卷积神经网络用到的backpropagation方法。也就是将输出层的误差 Cost ，求解各个权重的梯度 ∇U,∇V,∇W ，然后利用梯度下降法更新各个权重。现在问题就是如何求解各个权重的梯度，其它的所有东西都在之前介绍中谈到了，所有的trick都可以复用。
由于是序列化预测，那么对于每一时刻 t ，网络的输出 ot 都会产生一定误差 et ，误差的选择任君喜欢，可以是cross entropy也可以是平方误差等等。那么总的误差为 E=∑tet ，我们的目标就是要求取

∇U=∂E∂U=∑t∂et∂U∇V=∂E∂V=∑t∂et∂V∇W=∂E∂W=∑t∂et∂W

我们知道输出 ot=g(Vst) ,对于任意的 Cost 函数，求取 ∇V 将是简单的，我们可以直接求取每个时刻的 ∂et∂V ，由于它不存在和之前的状态依赖，可以直接求导取得，然后简单地求和即可。我们重点关注 ∇W,∇U 的计算。
回忆之前我们介绍多层感知器的backprop算法，我们知道算法的trick是定义一个 δ=∂e∂s ，首先计算出输出层的 δL ，再向后传播到各层 δL−1,δL−2,.... ，那么如何计算 δ 呢？先看下图：

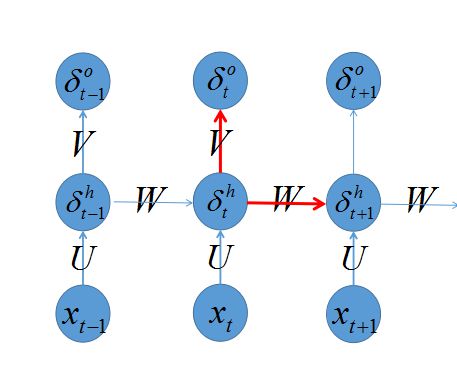
之前我们推导过，只要关注当前层次发射出去的链接即可，也就是

δht=(VTδot+WTδht+1).∗f′(st)

只要计算出所有的 δot,δht ，就可以通过以下计算出 ∇W,∇U ：

∇W=∑tδht×ht∇U=∑tδht×xt

其中 × 表示两个向量的外积。这样看来，只要你熟悉MLP的backprop算法，RNN写起程序来和MLP根本没有多大差异！手写naive的demo至少比CNN容易很多。

RNN的训练困难

虽然上一节中，我们强调了RNN的训练程序和MLP没太大差异，虽然写程序容易，但是训练起来却是千难万阻。为什么呢？因为我们的网络是根据输入而展开的，输入越长，展开的网络越深，那么对于“深度”网络训练有什么困难呢？最常见的是“gradient explode”和“gradient vanish”。这种问题在RNN中如何体现呢？为了强调这个问题，我们模仿Yoshua Bengio的论文《On the difficulty of training recurrent neural networks》的推导，重写一下RNN的梯度求解过程，为了推导方便，我们人为地为 W,U 打上标签 Wt,Ut ，即认为当确定好时间长度 T ，RNN就变成普通的MLP。打上标签后的RNN变成如下：

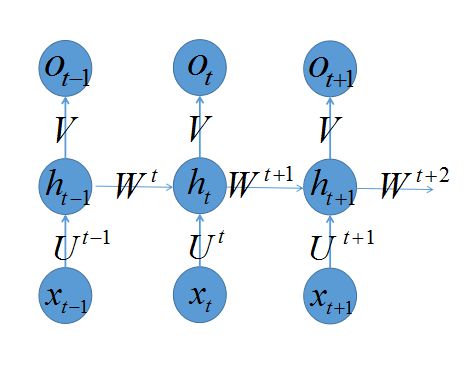
假如对于时刻 t+1 产生的误差 et+1 ，我们想计算它对于 W1,W2,....,Wt，Wt+1 的梯度，可以如下计算：

∂et+1∂Wt+1=∂et+1∂ht+1∂ht+1∂Wt+1

∂et+1∂Wt=∂et+1∂ht+1∂ht+1∂ht∂ht∂Wt

∂et+1∂Wt−1=∂et+1∂ht+1∂ht+1∂ht∂ht∂ht−1∂ht−1∂Wt−1

......

反复运用链式法则，我们可以求出每一个 ∇W1,∇W2,....,∇Wt，∇Wt+1 ，需要注意的是，实际RNN模型对于 W,U 都是不打标签的，也就是在不同时刻都是共享同样的参数，这样可以大大减少训练参数，和CNN的共享权重类似。对于共享参数的RNN，我们只需将上述的一系列式子抹去标签并求和，就可以得到Yoshua Bengio论文中所推导的梯度计算式子：

∂et∂W=∑1≤k≤t∂et∂ht∏k<i≤t∂hi∂hi−1∂+hk∂W

其中 ∂+hk∂W 代表不利用链式法则直接求导，也就是假如对于函数 f(h(x)) ，对其直接求导结果如下：

∂f(h(x))∂x=f′(h(x))

也就是将 h(x) 看成常数了。网上许多RNN教程都用Yoshua Bengio类似的推导，却省略了这个小步骤，使得初学者常常搞得晕头转向，摸不着头脑。论文中证明了：

||∏k<i≤t∂hi∂hi−1||≤ηt−k

从而说明了这是梯度求导的一部分环节是一个指数模型，当 η<1 时，就会出现”gradient vanish”问题，而当 η>1 时，“gradient explode”也就产生了。为了克服这样的问题，LSTM和GRU模型便后续被推出了。有趣的是，正是因为训练深度网络的困难，才导致神经网络这种古老模型沉寂了几十年，不过现在硬件的发展，训练数据的增多，神经网络重新得以复苏，并以重新以深度学习的外号杀出江湖。

参考引用

《Recurrent Neural Networks Tutorial》
《On the difficulty of training recurrent neural networks》

下面是RNNs的应用介绍，值得一看。转自：http://blog.csdn.net/heyongluoyao8/article/details/48636251

循环神经网络(RNN, Recurrent Neural Networks)介绍

   这篇文章很多内容是参考：http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/，在这篇文章中，加入了一些新的内容与一些自己的理解。

  循环神经网络(Recurrent Neural Networks，RNNs)已经在众多自然语言处理(Natural Language Processing, NLP)中取得了巨大成功以及广泛应用。但是，目前网上与RNNs有关的学习资料很少，因此该系列便是介绍RNNs的原理以及如何实现。主要分成以下几个部分对RNNs进行介绍：
1. RNNs的基本介绍以及一些常见的RNNs(本文内容)；
2. 详细介绍RNNs中一些经常使用的训练算法，如Back Propagation Through Time(BPTT)、Real-time Recurrent Learning(RTRL)、Extended Kalman Filter(EKF)等学习算法，以及梯度消失问题(vanishing gradient problem)
3. 详细介绍Long Short-Term Memory(LSTM，长短时记忆网络)；
4. 详细介绍Clockwork RNNs(CW-RNNs，时钟频率驱动循环神经网络)；
5. 基于Python和Theano对RNNs进行实现，包括一些常见的RNNs模型。

  不同于传统的FNNs(Feed-forward Neural Networks，前向反馈神经网络)，RNNs引入了定向循环，能够处理那些输入之间前后关联的问题。定向循环结构如下图所示：

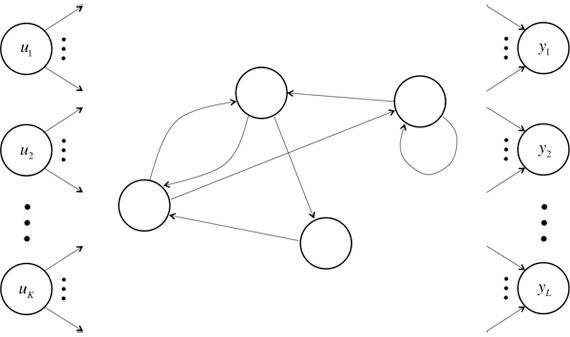
  该tutorial默认读者已经熟悉了基本的神经网络模型。如果不熟悉，可以点击：Implementing A Neural Network From Scratch进行学习。

什么是RNNs

  RNNs的目的使用来处理序列数据。在传统的神经网络模型中，是从输入层到隐含层再到输出层，层与层之间是全连接的，每层之间的节点是无连接的。但是这种普通的神经网络对于很多问题却无能无力。例如，你要预测句子的下一个单词是什么，一般需要用到前面的单词，因为一个句子中前后单词并不是独立的。RNNs之所以称为循环神经网路，即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。理论上，RNNs能够对任何长度的序列数据进行处理。但是在实践中，为了降低复杂性往往假设当前的状态只与前面的几个状态相关，下图便是一个典型的RNNs：

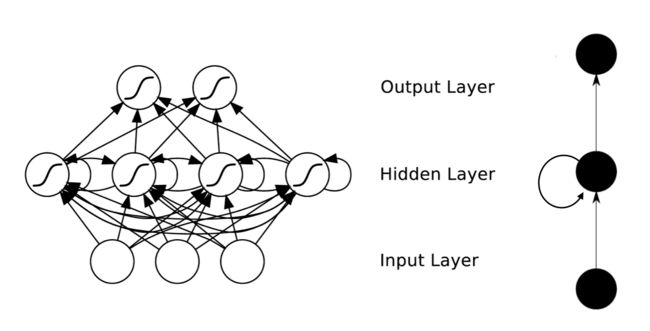
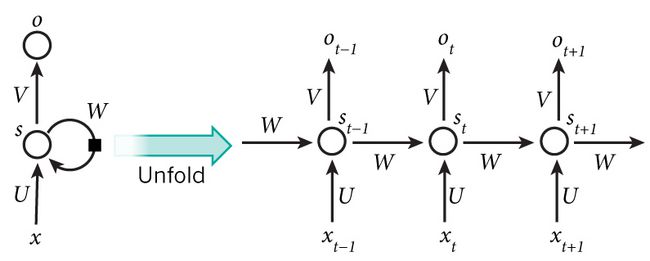
From Nature
  RNNs包含输入单元(Input units)，输入集标记为 {x0,x1,...,xt,xt+1,...} ，而输出单元(Output units)的输出集则被标记为 {y0,y1,...,yt,yt+1.,..} 。RNNs还包含隐藏单元(Hidden units)，我们将其输出集标记为 {s0,s1,...,st,st+1,...} ，这些隐藏单元完成了最为主要的工作。你会发现，在图中：有一条单向流动的信息流是从输入单元到达隐藏单元的，与此同时另一条单向流动的信息流从隐藏单元到达输出单元。在某些情况下，RNNs会打破后者的限制，引导信息从输出单元返回隐藏单元，这些被称为“Back Projections”，并且隐藏层的输入还包括上一隐藏层的状态，即隐藏层内的节点可以自连也可以互连。
  上图将循环神经网络进行展开成一个全神经网络。例如，对一个包含5个单词的语句，那么展开的网络便是一个五层的神经网络，每一层代表一个单词。对于该网络的计算过程如下：

• xt 表示第 t,t=1,2,3... 步(step)的输入。比如， x1 为第二个词的one-hot向量(根据上图， x0 为第一个词)；
  PS：使用计算机对自然语言进行处理，便需要将自然语言处理成为机器能够识别的符号，加上在机器学习过程中，需要将其进行数值化。而词是自然语言理解与处理的基础，因此需要对词进行数值化，词向量(Word Representation，Word embeding)[1]便是一种可行又有效的方法。何为词向量，即使用一个指定长度的实数向量v来表示一个词。有一种种最简单的表示方法，就是使用One-hot vector表示单词，即根据单词的数量|V|生成一个|V| * 1的向量，当某一位为一的时候其他位都为零，然后这个向量就代表一个单词。缺点也很明显：
  
  1. 由于向量长度是根据单词个数来的，如果有新词出现，这个向量还得增加，麻烦！(Impossible to keep up to date);
  2. 主观性太强(subjective)
  3. 这么多单词，还得人工打labor并且adapt，想想就恐
  4. 最不能忍受的一点便是很难计算单词之间的相似性。
     现在有一种更加有效的词向量模式，该模式是通过神经网或者深度学习对词进行训练，输出一个指定维度的向量，该向量便是输入词的表达。如word2vec。
• st 为隐藏层的第 t 步的状态，它是网络的记忆单元。 st 根据当前输入层的输出与上一步隐藏层的状态进行计算。 st=f(Uxt+Wst−1) ，其中 f 一般是非线性的激活函数，如tanh或ReLU，在计算 s0 时，即第一个单词的隐藏层状态，需要用到 s−1 ，但是其并不存在，在实现中一般置为0向量；
• ot 是第 t 步的输出，如下个单词的向量表示， ot=softmax(Vst) .
  需要注意的是：
• 你可以认为隐藏层状态 st 是网络的记忆单元. st 包含了前面所有步的隐藏层状态。而输出层的输出 ot 只与当前步的 st 有关，在实践中，为了降低网络的复杂度，往往 st 只包含前面若干步而不是所有步的隐藏层状态；
• 在传统神经网络中，每一个网络层的参数是不共享的。而在RNNs中，每输入一步，每一层各自都共享参数 U,V,W 。其反应者RNNs中的每一步都在做相同的事，只是输入不同，因此大大地降低了网络中需要学习的参数；这里并没有说清楚，解释一下，传统神经网络的参数是不共享的，并不是表示对于每个输入有不同的参数，而是将RNN是进行展开，这样变成了多层的网络，如果这是一个多层的传统神经网络，那么 xt 到 st 之间的U矩阵与 xt+1 到 st+1 之间的 U 是不同的，而RNNs中的却是一样的，同理对于 s 与 s 层之间的 W 、 s 层与 o 层之间的 V 也是一样的。
• 上图中每一步都会有输出，但是每一步都要有输出并不是必须的。比如，我们需要预测一条语句所表达的情绪，我们仅仅需要关系最后一个单词输入后的输出，而不需要知道每个单词输入后的输出。同理，每步都需要输入也不是必须的。RNNs的关键之处在于隐藏层，隐藏层能够捕捉序列的信息。

RNNs能干什么？

  RNNs已经被在实践中证明对NLP是非常成功的。如词向量表达、语句合法性检查、词性标注等。在RNNs中，目前使用最广泛最成功的模型便是LSTMs(Long Short-Term Memory，长短时记忆模型)模型，该模型通常比vanilla RNNs能够更好地对长短时依赖进行表达，该模型相对于一般的RNNs，只是在隐藏层做了手脚。对于LSTMs，后面会进行详细地介绍。下面对RNNs在NLP中的应用进行简单的介绍。

语言模型与文本生成(Language Modeling and Generating Text)

  给你一个单词序列，我们需要根据前面的单词预测每一个单词的可能性。语言模型能够一个语句正确的可能性，这是机器翻译的一部分，往往可能性越大，语句越正确。另一种应用便是使用生成模型预测下一个单词的概率，从而生成新的文本根据输出概率的采样。语言模型中，典型的输入是单词序列中每个单词的词向量(如 One-hot vector)，输出时预测的单词序列。当在对网络进行训练时，如果 ot＝xt+1 ，那么第 t 步的输出便是下一步的输入。
  下面是RNNs中的语言模型和文本生成研究的三篇文章：

• Recurrent neural network based language model
• Extensions of Recurrent neural network based language model
• Generating Text with Recurrent Neural Networks

机器翻译(Machine Translation)

  机器翻译是将一种源语言语句变成意思相同的另一种源语言语句，如将英语语句变成同样意思的中文语句。与语言模型关键的区别在于，需要将源语言语句序列输入后，才进行输出，即输出第一个单词时，便需要从完整的输入序列中进行获取。机器翻译如下图所示：

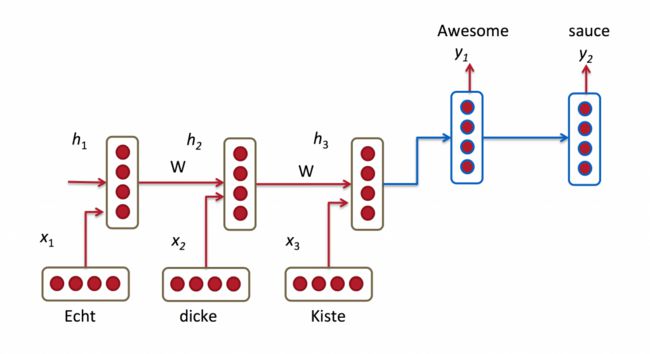
RNN for Machine Translation. Image Source
  下面是关于RNNs中机器翻译研究的三篇文章：

• A Recursive Recurrent Neural Network for Statistical Machine Translation
• Sequence to Sequence Learning with Neural Networks
• Joint Language and Translation Modeling with Recurrent Neural Networks

语音识别(Speech Recognition)

  语音识别是指给一段声波的声音信号，预测该声波对应的某种指定源语言的语句以及该语句的概率值。
  RNNs中的语音识别研究论文：

• Towards End-to-End Speech Recognition with Recurrent Neural Networks

图像描述生成 (Generating Image Descriptions)

  和卷积神经网络(convolutional Neural Networks, CNNs)一样，RNNs已经在对无标图像描述自动生成中得到应用。将CNNs与RNNs结合进行图像描述自动生成。这是一个非常神奇的研究与应用。该组合模型能够根据图像的特征生成描述。如下图所示：

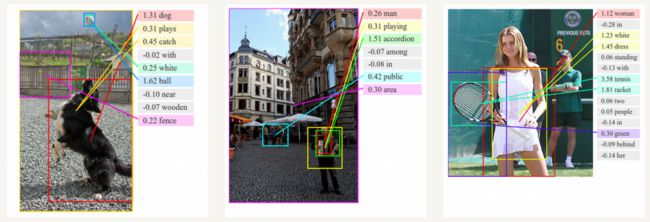
  图像描述生成中的深度视觉语义对比. Image Source

如何训练RNNs

  对于RNN是的训练和对传统的ANN训练一样。同样使用BP误差反向传播算法，不过有一点区别。如果将RNNs进行网络展开，那么参数 W,U,V 是共享的，而传统神经网络却不是的。并且在使用梯度下降算法中，每一步的输出不仅依赖当前步的网络，并且还以来前面若干步网络的状态。比如，在 t=4 时，我们还需要向后传递三步，已经后面的三步都需要加上各种的梯度。该学习算法称为Backpropagation Through Time (BPTT)。后面会对BPTT进行详细的介绍。需要意识到的是，在vanilla RNNs训练中，BPTT无法解决长时依赖问题(即当前的输出与前面很长的一段序列有关，一般超过十步就无能为力了)，因为BPTT会带来所谓的梯度消失或梯度爆炸问题(the vanishing/exploding gradient problem)。当然，有很多方法去解决这个问题，如LSTMs便是专门应对这种问题的。

RNNs扩展和改进模型

  这些年，研究者们已经提出了多钟复杂的RNNs去改进vanilla RNN模型的缺点。下面是目前常见的一些RNNs模型，后面会对其中使用比较广泛的进行详细讲解，在这里进行简单的概述。

Simple RNNs(SRNs)[2]

  SRNs是RNNs的一种特例，它是一个三层网络，并且在隐藏层增加了上下文单元，下图中的 y 便是隐藏层， u 便是上下文单元。上下文单元节点与隐藏层中的节点的连接是固定(谁与谁连接)的，并且权值也是固定的(值是多少)，其实是一个上下文节点与隐藏层节点一一对应，并且值是确定的。在每一步中，使用标准的前向反馈进行传播，然后使用学习算法进行学习。上下文每一个节点保存其连接的隐藏层节点的上一步的输出，即保存上文，并作用于当前步对应的隐藏层节点的状态，即隐藏层的输入由输入层的输出与上一步的自己的状态所决定的。因此SRNs能够解决标准的多层感知机(MLP)无法解决的对序列数据进行预测的任务。
  SRNs网络结构如下图所示：

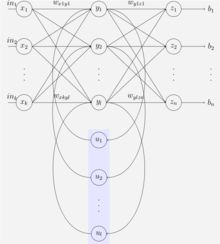
Bidirectional RNNs[3]

  Bidirectional RNNs(双向网络)的改进之处便是，假设当前的输出(第 t 步的输出)不仅仅与前面的序列有关，并且还与后面的序列有关。例如：预测一个语句中缺失的词语那么就需要根据上下文来进行预测。Bidirectional RNNs是一个相对较简单的RNNs，是由两个RNNs上下叠加在一起组成的。输出由这两个RNNs的隐藏层的状态决定的。如下图所示：

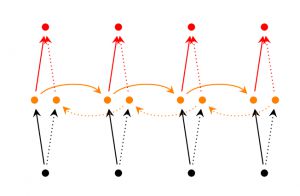
Deep(Bidirectional)RNNs[4]

  Deep(Bidirectional)RNNs与Bidirectional RNNs相似，只是对于每一步的输入有多层网络。这样，该网络便有更强大的表达与学习能力，但是复杂性也提高了，同时需要更多的训练数据。Deep(Bidirectional)RNNs的结构如下图所示：

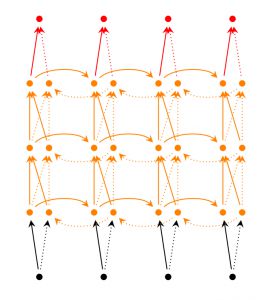
Echo State Networks[5]

  ESNs(回声状态网络)虽然也是一种RNNs，但是它与传统的RNNs相差很大。ESNs具有三个特点：

• 它的核心结构时一个随机生成、且保持不变的储备池(Reservoir)，储备池是大规模的、随机生成的、稀疏连接(SD通常保持1%～5%，SD表示储备池中互相连接的神经元占总的神经元个数N的比例)的循环结构；
• 其储备池到输出层的权值矩阵是唯一需要调整的部分；
• 简单的线性回归就可完成网络的训练。

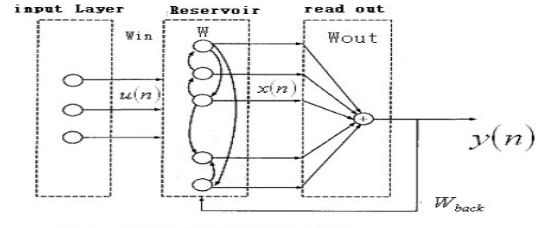
  从结构上讲，ESNs是一种特殊类型的循环神经网络，其基本思想是：使用大规模随机连接的循环网络取代经典神经网络中的中间层，从而简化网络的训练过程。因此ESNs的关键是中间的储备池。网络中的参数包括： W 为储备池中节点的连接权值矩阵， Win 为输入层到储备池之间的连接权值矩阵，表明储备池中的神经元之间是连接的， Wback 为输出层到储备池之间的反馈连接权值矩阵，表明储备池会有输出层来的反馈， Wout 为输入层、储备池、输出层到输出层的连接权值矩阵，表明输出层不仅与储备池连接，还与输入层和自己连接。 Woutbias 表示输出层的偏置项。
  对于ESNs，关键是储备池的四个参数，如储备池内部连接权谱半径SR( SR=λmax=max{|W的特征指|} ，只有SR <1时，ESNs才能具有回声状态属性)、储备池规模N(即储备池中神经元的个数)、储备池输入单元尺度IS(IS为储备池的输入信号连接到储备池内部神经元之前需要相乘的一个尺度因子)、储备池稀疏程度SD(即为储备池中互相连接的神经元个数占储备池神经元总个数的比例)。对于IS，如果需要处理的任务的非线性越强，那么输入单元尺度越大。该原则的本质就是通过输入单元尺度IS，将输入变换到神经元激活函数相应的范围(神经元激活函数的不同输入范围，其非线性程度不同)。
  ESNs的结构如下图所示：

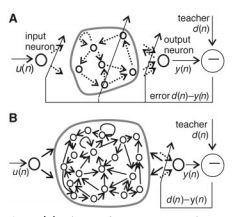
Gated Recurrent Unit Recurrent Neural Networks[6]

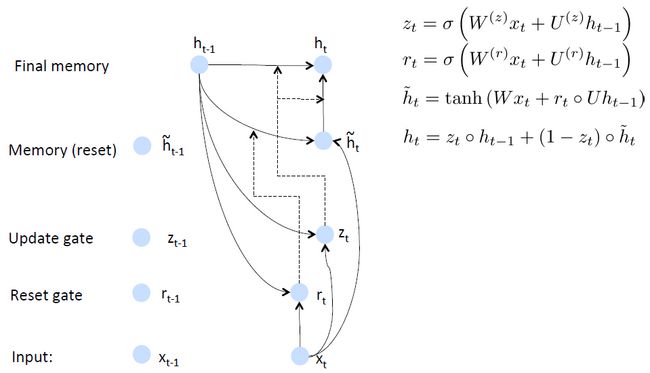
  GRUs也是一般的RNNs的改良版本，主要是从以下两个方面进行改进。一是，序列中不同的位置处的单词(已单词举例)对当前的隐藏层的状态的影响不同，越前面的影响越小，即每个前面状态对当前的影响进行了距离加权，距离越远，权值越小。二是，在产生误差error时，误差可能是由某一个或者几个单词而引发的，所以应当仅仅对对应的单词weight进行更新。GRUs的结构如下图所示。GRUs首先根据当前输入单词向量word vector已经前一个隐藏层的状态hidden state计算出update gate和reset gate。再根据reset gate、当前word vector以及前一个hidden state计算新的记忆单元内容(new memory content)。当reset gate为1的时候，new memory content忽略之前的所有memory content，最终的memory是之前的hidden state与new memory content的结合。

LSTM Netwoorks[7]

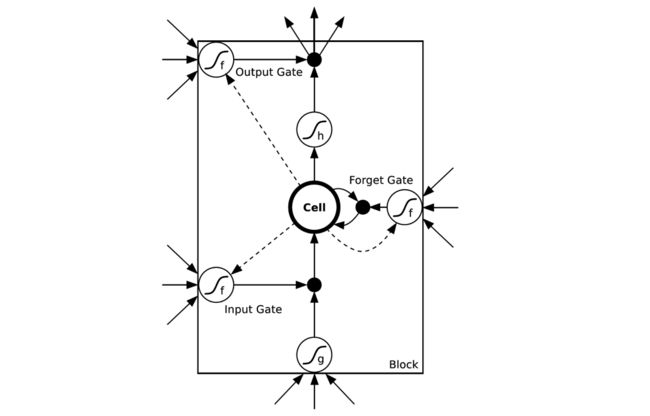
  LSTMs与GRUs类似，目前非常流行。它与一般的RNNs结构本质上并没有什么不同，只是使用了不同的函数去去计算隐藏层的状态。在LSTMs中，i结构被称为cells，可以把cells看作是黑盒用以保存当前输入 xt 之前的保存的状态 ht−1 ，这些cells更加一定的条件决定哪些cell抑制哪些cell兴奋。它们结合前面的状态、当前的记忆与当前的输入。已经证明，该网络结构在对长序列依赖问题中非常有效。LSTMs的网络结构如下图所示。对于LSTMs的学习，参见this post has an excellent explanation



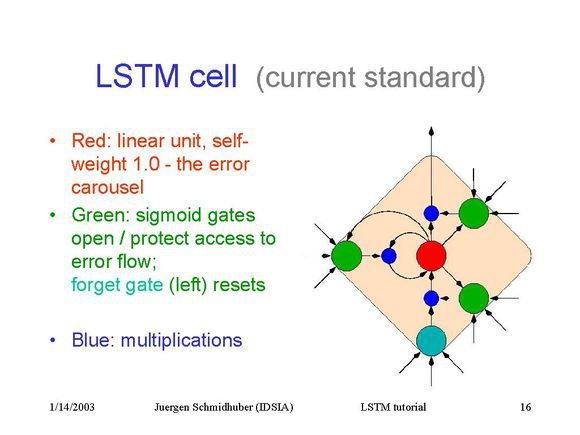
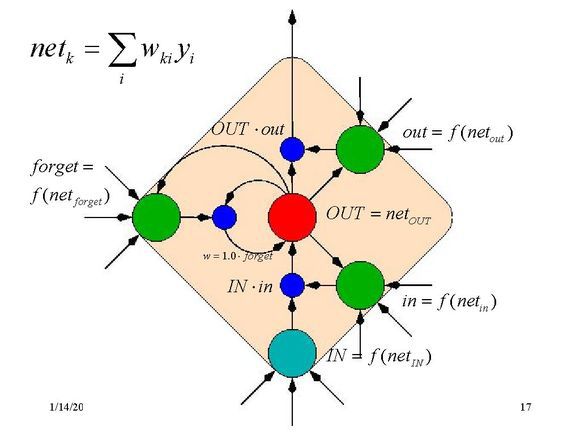
  LSTMs解决的问题也是GRU中所提到的问题，如下图所示：

  LSTMs与GRUs的区别如图所示[8]：

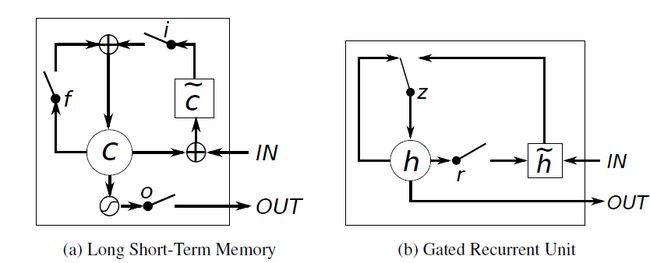
  从上图可以看出，它们之间非常相像，不同在于：

• new memory的计算方法都是根据之前的state及input进行计算，但是GRUs中有一个reset gate控制之前state的进入量，而在LSTMs里没有这个gate；
• 产生新的state的方式不同，LSTMs有两个不同的gate，分别是forget gate (f gate)和input gate(i gate)，而GRUs只有一个update gate(z gate)；
• LSTMs对新产生的state又一个output gate(o gate)可以调节大小，而GRUs直接输出无任何调节。

Clockwork RNNs(CW-RNNs)[9]

  CW-RNNs是较新的一种RNNs模型，其论文发表于2014年Beijing ICML。在原文[8]中作者表示其效果较SRN与LSTMs都好。
  CW-RNNs也是一个RNNs的改良版本，是一种使用时钟频率来驱动的RNNs。它将隐藏层分为几个块(组，Group/Module)，每一组按照自己规定的时钟频率对输入进行处理。并且为了降低标准的RNNs的复杂性，CW-RNNs减少了参数的数目，提高了网络性能，加速了网络的训练。CW-RNNs通过不同的隐藏层模块工作在不同的时钟频率下来解决长时间依赖问题。将时钟时间进行离散化，然后在不同的时间点，不同的隐藏层组在工作。因此，所有的隐藏层组在每一步不会都同时工作，这样便会加快网络的训练。并且，时钟周期小的组的神经元的不会连接到时钟周期大的组的神经元，只会周期大的连接到周期小的(认为组与组之间的连接是有向的就好了，代表信息的传递是有向的)，周期大的速度慢，周期小的速度快，那么便是速度慢的连速度快的，反之则不成立。现在还不明白不要紧，下面会进行讲解。
   CW-RNNs与SRNs网络结构类似，也包括输入层(Input)、隐藏层(Hidden)、输出层(Output)，它们之间也有向前连接，输入层到隐藏层的连接，隐藏层到输出层的连接。但是与SRN不同的是，隐藏层中的神经元会被划分为若干个组，设为 g ，每一组中的神经元个数相同，设为 k ，并为每一个组分配一个时钟周期 Ti∈{T1,T2,...,Tg} ，每一个组中的所有神经元都是全连接，但是组 j 到组 i 的循环连接则需要满足 Tj 大于 Ti 。如下图所示，将这些组按照时钟周期递增从左到右进行排序，即 T1<T2<...<Tg ，那么连接便是从右到左。例如：隐藏层共有256个节点，分为四组，周期分别是[1,2,4,8]，那么每个隐藏层组256/4=64个节点，第一组隐藏层与隐藏层的连接矩阵为64*64的矩阵，第二层的矩阵则为64*128矩阵，第三组为64*(3*64)=64*192矩阵，第四组为64*(4*64)=64*256矩阵。这就解释了上一段的后面部分，速度慢的组连到速度快的组，反之则不成立。
  CW-RNNs的网络结构如下图所示：

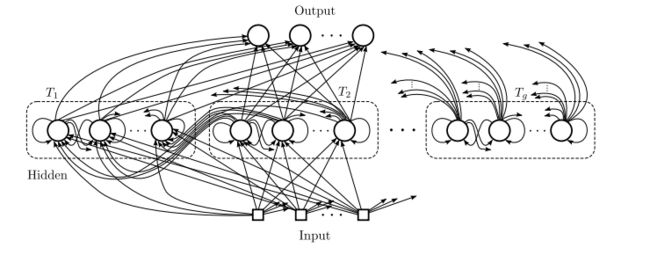
  在传统的RNN中，按照下面的公式进行计算：

st=fs(Wst−1+Winxt)

ot=fo(Woutst)

  其中， W 为隐藏层神经元的自连接矩阵， Win 为输入层到隐藏层的连接权值矩阵， Wout 是隐藏层到输出层的连接权值矩阵 ， xt 是第 t 步的输入， st−1 为第 t−1 步隐藏层的输出， st 为第 t 步隐藏层的输出， ot 为第 t 步的输出， fs 为隐藏层的激活函数， fo 为输出层的激活函数。
  与传统的RNNs不同的是，在第 t 步时，只有那些满足 (tmodTi)=0 的隐藏层组才会执行。并且每一隐藏层组的周期 {T1,T2,...,Tg} 都可以是任意的。原文中是选择指数序列作为它们的周期，即 Ti=2i−1i∈[1,...,g] 。
  因此 W 与 Win 将被划分为 g 个块。如下：

W=⎡⎣⎢W1...Wg⎤⎦⎥

Win=⎡⎣⎢Win1...Wing⎤⎦⎥

其中 W 是一个上三角矩阵，每一个组行 Wi 被划分为列向量 {W1i,...,Wii,0(i+1)i,...,0gi}T ， Wji,j∈[1,...,g] 表示第i个组到第j个组的连接权值矩阵。在每一步中， W 与 Win 只有部分组行处于执行状态，其它的为0：

Wi={Wi0,for(tmodTi)=0,otherwise

Wini={Wini0,for(tmodTi)=0,otherwise

  为了使表达不混淆，将 Win 写成 Win 。并且执行的组所对应的 o 才会有输出。处于非执行状态下的隐藏层组仍保留着上一步的状态。下图是含五个隐藏层组在 t=6 时的计算图：

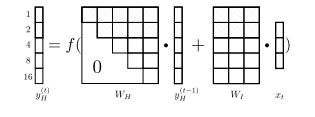
  在CW-RNNs中，慢速组(周期大的组)处理、保留、输出长依赖信息，而快速组则会进行更新。CW-RNNs的误差后向传播也和传统的RNNs类似，只是误差只在处于执行状态的隐藏层组进行传播，而非执行状态的隐藏层组也复制其连接的前面的隐藏层组的后向传播。即执行态的隐藏层组的误差后向传播的信息不仅来自与输出层，并且来自与其连接到的左边的隐藏层组的后向传播信息，而非执行态的后向传播信息只来自于其连接到的左边的隐藏层组的后向传播数据。
  下图是原文对三个不同RNNs模型的实验结果图：

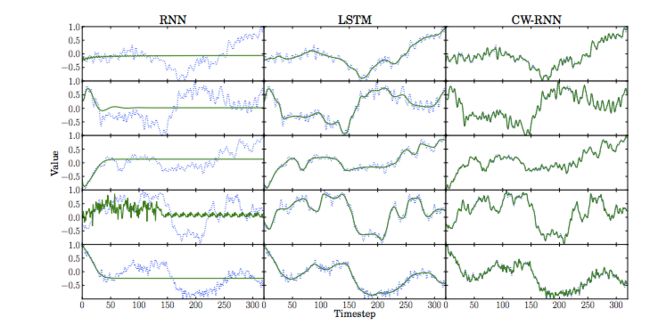
  上图中，绿色实线是预测结果，蓝色散点是真实结果。每个模型都是对前半部分进行学习，然后预测后半部分。LSTMs模型类似滑动平均，但是CW-RNNs效果更好。其中三个模型的输入层、隐藏层、输出层的节点数都相同，并且只有一个隐藏层，权值都使用均值为0，标准差为0.1的高斯分布进行初始化，隐藏层的初始状态都为0，每一个模型都使用 Nesterov-style
momentum SGD(Stochastic Gradient Descent，随机梯度下降算法)[10]进行学习与优化。

总结

  到目前为止，本文对RNNs进行了基本的介绍，并对常见的几种RNNs模型进行了初步讲解。下一步将基于Theano与Python实现一个RNNs语言模型并对上面的一些RNNs模型进行详解。这里有更多的RNNs模型。

  后面将陆续推出：

• 详细介绍RNNs中一些经常使用的训练算法，如Back Propagation Through Time(BPTT)、Real-time Recurrent Learning(RTRL)、Extended Kalman Filter(EKF)等学习算法，以及梯度消失问题(vanishing gradient problem)
• 详细介绍Long Short-Term Memory(LSTM，长短时记忆网络)；
• 详细介绍Clockwork RNNs(CW-RNNs，时钟频率驱动循环神经网络)；
• 基于Python和Theano对RNNs进行实现，包括一些常见的RNNs模型；

  本系列将实现一个基于循环神经网络的语言模型(recurrent neural network based language model)。该实现包含两个方面：一是能够得到任意语句在现实中成立的得分，其提供了判断语法与语义的正确性的度量方式。该模型是机器翻译中的典型应用。二是模型能够产生新的文本，这是一个非常棒的应用。比如，对莎士比亚的文章进行训练，能够产生一个新的类似莎士比亚的文本，目前，这个有趣的想法已经被Andrew Karpathy基于RNNs的字符级别的语言模型实现了。

参考博文

http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/

参考文献

[1] Hinton G E. Learning Distributed Representations of Concepts[C]. Proceedings of the 8th Annual Conference of the Cognitive Science Society. 1986, 1: 12.
[2] Elman, J. L. Finding structure in time. CRL Technical Report 8801, Center for Research in Language, University
of California, San Diego, 1988.
[3] Schuster M, Paliwal K K. Bidirectional recurrent neural networks[J]. Signal Processing, IEEE Transactions on, 1997, 45(11): 2673-2681.
[4] Graves A, Mohamed A R, Hinton G. Speech Recognition with Deep Recurrent Neural Networks[J]. Acoustics Speech & Signal Processing . icassp. international Conference on, 2013:6645 - 6649.
[5] Jaeger H, Haas H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication[J]. Science, 2004, 304(5667): 78-80.
[6] Cho K, Van Merrienboer B, Gulcehre C, et al. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation[J]. Eprint Arxiv, 2014.
[7] Hochreiter S, Schmidhuber J. Long short-term memory.[J]. Neural Computation, 1997, 9(8):1735-1780.
[8] Chung J, Gulcehre C, Cho K H, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[J]. arXiv preprint arXiv:1412.3555, 2014.
[9] Jan Koutnik, Klaus Greff, Faustino Gomez, Juergen Schmidhuber. A Clockwork RNN[J]. Proceedings of The 31st International Conference on Machine Learning, pp. 1863–1871, 2014.
[10] Sutskever, Ilya, Martens, James, Dahl, George E., and Hinton, Geoffrey E. On the importance of initialization and momentum in deep learning. In Dasgupta, Sanjoy and Mcallester, David (eds.), Proceedings of the 30th International Conference on Machine Learning (ICML-13), volume 28, pp. 1139–1147.