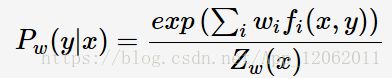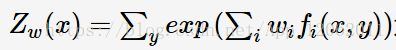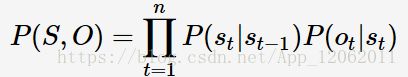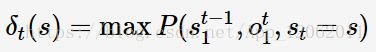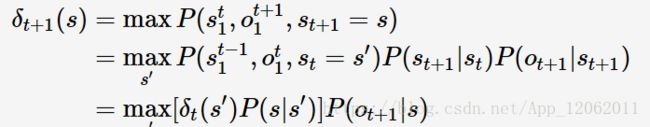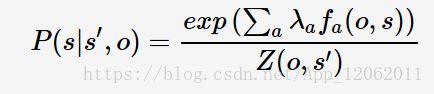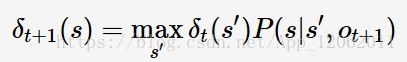系统学习机器学习之随机场(二)--MEMM

     最大熵模型（Maximum Entropy Models, MaxEnt）是基于大熵理论的统计模型， 广泛应用于模式识别和统计评估中。最大熵原理有一个很长的历史，其中最大熵理论方面的先驱 E.T.Jaynes 在 1990 年给出了最大熵原理的基本属性：最大熵概率分布服从我们已知的不完整信息的约束。主要思想是，在用有限知识预测未知时，不做任何有偏的假设。根据熵的定义，一个随机变量的不确定性是由熵体现的，熵最大时随机变量最不确定，对其行为做准确预测最困难。最大熵原理的实质是，在已知部分知识前提下，关于未知分布最合理的推断是符合已知知识的最不确定或最随机的推断，这是我们可以做出的唯一不偏不倚的选 择。最大熵的原理可以概括为，将已知事件作为约束条件，求得可使熵最大化的概率分布作为正确的概率分布。对于最大熵的约束条件，应用在熵的计算公式时，我们希望找到能同时满足多个约束条件的最均匀模型。也就是在约束条件下，熵取得最大值。如何在给定约束集条件下，求得最优最大熵模型？

这里，我们直接给出最大熵模型的约束条件：

经验期望和模型期望相等，即模型的约束等式。

满足约束条件的模型很多。模型的目标是产生在约束集下具有均匀分布的模型，条件熵 H( X|Y)作为条件概率P(y|x)均匀性的一种数学测度方法。为了强调熵对概率分布 p 的依赖，我们用H(P)代替H(Y|X):

 

对于任意给定的约束集C ，能找到唯一的P*使H（p)取得大值，如何找到p*， 是一个约束最优化问题。我们给出p* 的等式：

对于简单的约束条件，我们能用解析的方法找到最优的概率分布，但对于一般性问题， 这种方法是不可行的。为解决一般性约束最优化问题，我们应用了约束最优化理论中的 Lagrange 乘子定理解决这个问题，具体推导这里不补充了。类似SVM的对偶求解。

具体化这个模型：

最大熵（Maximum Entropy）模型属于log-linear model，在给定训练数据的条件下对模型进行极大似然估计或正则化极大似然估计：

其中Z是归一化因子：

实际上，你可以看出，该模型实际为softmax，也就是说，MaxEnt是多元逻辑归回在某个角度等价，因为多元逻辑回归的极大似然估计，正好得到了最大熵。《自然语言处理综论》这本书里，MaxEnt就是用逻辑回归推导出来的，也就是说在语音和语言处理中，多元逻辑回归称为最大熵模型。

这里的f(x,y)是二值分段函数，表示输入x与标签y之间的二值。要想成功的使用MaxEnt，关键在于设计恰当的特征和特征组合。

最大熵没有假设特征之间独立，因此，用户选择特征灵活。

为什么称为最大熵？

是因为从直觉上来说，所谓的最大熵，就是通过不断增加特征的方法，来建立分布。而最大熵的最优化问题的解（也就是极大似然估计出的参数）就是多元逻辑回归的分布，它的权值W把训练数据的似然度最大化。因此，当根据最大似然度的标准来训练时，多元逻辑回归的指数模型也能找到最大熵，这个最大熵分布服从来自特征函数的约束。

MEMM（Maximum Entropy Markov Model）

MEMM实际上，一句话总结就是 ，在HMM中，计算后验概率时，采用贝叶斯定理来计算，也就是通过先验概率和似然度的乘积来计算，MEMM直接估计后验概率。

因为HMM需要的混淆矩阵是概率形式，MaxEnt正好把一个单独的观察分类到离散类别集合的一个成分中去，

区别过程如下：

HMM:

其中，S、O分别表示状态序列与观测序列。HMM的解码问题为argmaxP(S|O)；定义在时刻t状态为s的所有单个路径st1中的概率最大值为:

则有:

上述式子即为（用于解决HMM的解码问题的）Viterbi算法的递推式；可以看出HMM是通过联合概率来求解标注问题的。

MEMM：

MEMM并没有像HMM通过联合概率建模，而是直接学习条件概率：

因此，有别于HMM，MEMM的当前状态依赖于前一状态与当前观测；HMM与MEMM的图模型如下（图来自于[3]）：

一般化条件概率（4）为P(s|s′,o)。MEMM用最大熵模型来学习条件概率(4)，套用模型(3)则有：

其中，λa为学习参数；a=且bb为feature，ss为destination state；特征函数fa(o,s)的示例如下（图出自于[6]）：

类似于HMM，MEMM的解码问题的递推式：

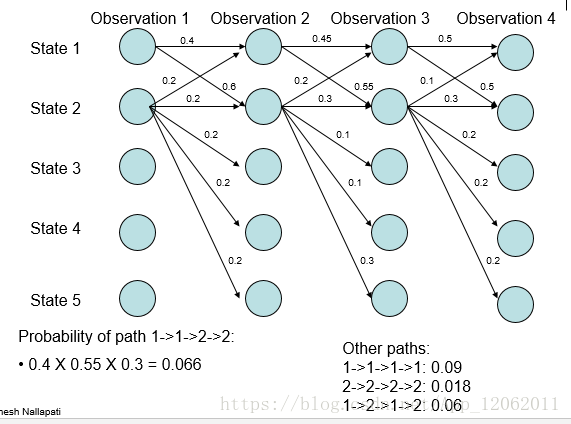
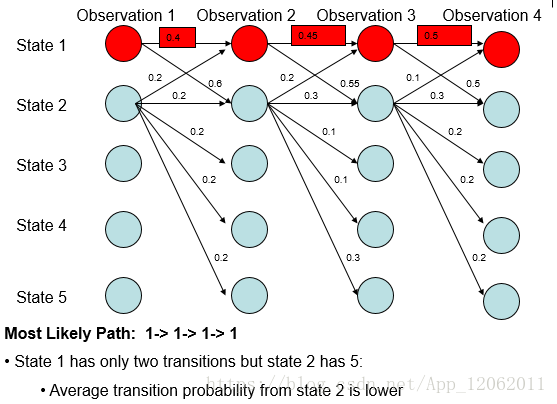
但是，MEMM存在着标注偏置问题（label bias problem）。比如，有如下的概率分布（图来自于[7])：

根据上述递推式，则概率最大路径如下：

但是，从全局的角度分析：

• 无论观测值，State 1 总是更倾向于转移到State 2；
• 无论观测值，State 2 总是更倾向于转移到State 2.

从式子(5)可以看出MEMM所做的是局部归一化，导致有更少转移的状态拥有的转移概率普遍偏高，概率最大路径更容易出现转移少的状态。因MEMM存在着标注偏置问题，故全局归一化的CRF被提了出来[3]。

总结：

我们可以看出，MEMM是对HMM的扩展增强，体现在如下方面：

1.HMM的存在问题

生成式模型

需要准确地计算出观测序列X和隐藏状态序列Y的联合概率，然而这会导致以下两个问题： 
1. 必须计算出所有的潜在可能路径的概率值大小（然后再挑概率值最大的那一个作为最终结果） 
2. 对于某些未定义的观测值（如分词问题中的未登录词）需要统一设置一个默认的概率值

缺乏灵活性

如果对于某一个观测值，它可能并非由一个隐藏状态决定的，而是两个以上的隐藏状态综合作用而产生的，那么这时HMM就无能为力了。 
比如说，对于词性标注问题，可能有这么两类非互斥的隐藏状态——1.是否首字母大写、2.是否以’er’结尾。

也就是说，生成模型计算P（x,y）必然要考虑特征之间的关系，HMM假设特征之间独立，也就是丢弃了特征之间的关系，降低了模型的正确性。但是，对特征之间关系建模，又很难实现。因此，MEMM用判别模式不考虑特征关系存在与否规避了这个问题。因此，比HMM更加合理。

也可以处理多种可同时出现的隐藏状态

一些HMM的高效算法（如维特比算法）可以直接拿过来用