用Python做证券指数的三种策略分析
这两天恰好看到一本比较有趣的书,《FOF组合基金》。讲的是Fund of Fund,讲的是组合基金的理论,架构和实践。可以说是有既有理论高度,又有实践的策略。
其中有段话比较值得玩味。“可行集中包括无数个可供投资者选择的证券投资组合。投资者可通过有效集定理来找到最佳的投资组合。所谓最佳投资组合。。。。。满足两个条件:
1、相同风险下具有最大收益率的投资组合
2、同样收益率的水平下具有最小风险的投资组合
实践中还有另外一个很重要的因子,资金容量
所有人都在寻找高收益率,低风险,大容量的策略。但遗憾的是三者不可兼得。。。。共有8种类型的策略。其中比较有代表性的是相对价值策略,事件驱动策略,宏观因素策略。
上周股市大涨,本周股市大跌。那么,现在以2月1日的收盘数据来看,指数中有哪些符合中三种策略的指数?
我尝试用Python和手中的数据做了一个简单基于Z值的分析,自我学习和分享讨论。
1 、相对价值策略。(低收益,低风险,高容量)
书中谈的相对价值策略主要是类固定收益(银行理财,货币基金,债卷,对冲套利等),代价是牺牲”收益率“,从而保证风险可控,和规模扩大。
书中谈的方法。基本上需要通过期货,期限套利,跨期套利,分级基金折价,溢价,ETF套利,可转债,波动率,期权等方式。也许这种方式就是雪球上 低风险投资的策略吧。
相对价值策略需要拥有广阔的知识面和大额的资金。而且2015年后,卷商的ETF交易系统接口已经关闭,ETF套利很难运行。未来发展有赖于接口系统重新开放。
既然那么复杂,我就把问题简单化。
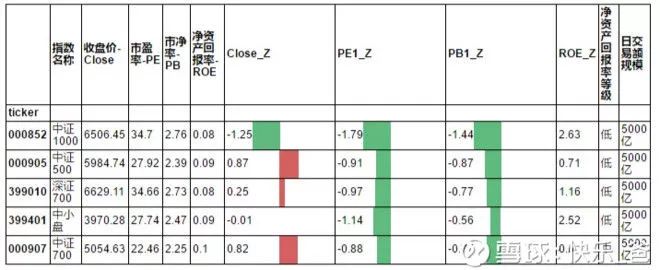
1.容量: 设为 500亿以上~5000亿日交易额规模。(盘子必须要大,流动性要好)
2.风险: 设为该日市盈率和市净率为Z值之和最小的5个指数。(风险要低)
3.收益率: 无所谓,可以牺牲。
结果如下: 找到的这5个指数的净资产收益率较低(小于10%),相对风险释放比较多(市盈率和市净率的Z值都是历史中的非常低位置),(盘子比较大(超过500亿)。其中以中证1000为最甚。
不过这里的风险最小,只是指数自己和自己历史比较的Z值。Z值可以衡量相对风险。绝对风险,也许只有FOF组合基金中讲的对冲,和组合等策略才能做到。
2、宏观因素策略。(高收益,高风险,高容量)
以牺牲风险为代价。。。也称择时策略。。。做对,自然收益会搞;但是如果做错,则损失也会很大。。。总的来说可以分成两类:拐点择时和趋势择时。
注: 这种策略应该就是人们常说的”投机“。
这些策略是技术流。利用了SVM(支持向量机)挖掘历史模型,Hurst指数,情绪指数,噪声指数等或者是各种均线等。
技术流暂且不研究,我们可以先看看市场中那些是宏观因素策略指数。把问题简化为:
1.高收益:ROE(PB/PB) 等级为高(15%~21%)(收益率必须要高。注:这里的收益率是长期的)
2.高容量: 50亿~500亿日交易额 (盘子必须要大,流动性要好)
3.高风险:(风险无所谓,可以适当放宽)
结果如下:
消费,食品,饮料等净资产回报率很高在20%左右,但是相对价格,市盈率,市净率的Z值有的都已经超过了3,或者4. 当这些指数回归均值时,估计要“疑似银河落九天”
不过创业成长指数,近资产汇报率19%,但是PB,PE的Z值都非常地。日后好好研究,看看是否是一支被错杀的创业板指数。
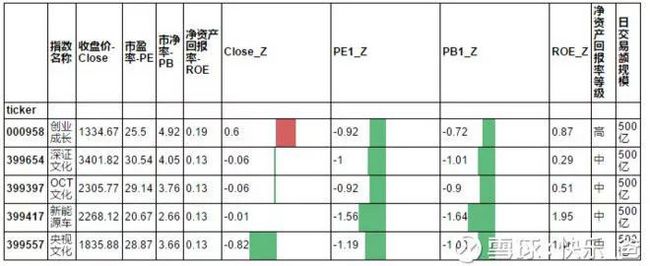
3、事件驱动策略(低风险,高收益,资金容量比较小)
把问题简化为:
1.低风险:当市净率,市盈率Z值最低
2.高收益: ROE(PB/PB) 较高的5只指数(收益率必须要高。注:这里的收益率是长期的)
3.容量: 不设限制
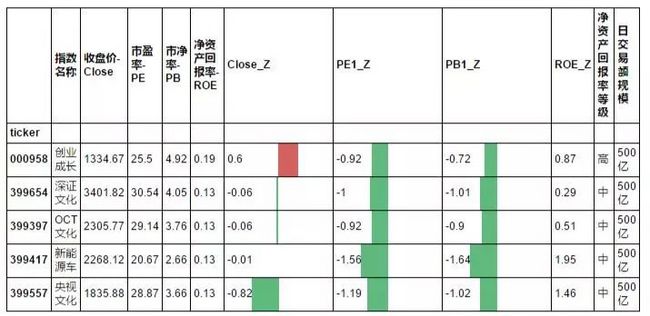
他们分别是创业成长,新能源车,和文化类指数。
新能源车由于补贴政策的变化,不断的估值调整,下滑。
文化类指数,由于乐视这个老鼠屎,整个系列都在过去两年垫底。
不过创业成长指数净资产回报率非常高,却估值很低,风险释放充分。
代码在后面:
1、初始化环境 主要用到了Python numpy,Pandas, Scipy.stats, Matplotlib,还有seaborn 等包. 证券投资的机器学习预测,通常需要准备大量数据进行回测。 本文不包含预测和回测部分。
注:预测和回测也没用。看了FOF组合基金一书才知道,2015年卷商交易接口已经关闭。估计ETF高频套利也不能做了。 此处如果理解有误,还请高人指点。
import pandas as pd
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
!free -h
# 以下代码是为了显示正文正常
import matplotlib as mpl
import matplotlib.font_manager as font_manager
path_eng = '/usr/share/fonts/chinese/REFSAN.TTF'
path_CHN = "/usr/share/fonts/chinese/simhei.ttf"
prop = font_manager.FontProperties(fname=path_CHN) #Set the microsoft sans serief as default font family. if show chinese test, set path_CHN instead.
#prop.set_weight = 'light'
mpl.rcParams['font.family'] = prop.get_name()
Today = "2018-02-01"
数据概览
def view_data():
print("数据载入中...")
sec_map = pd.read_hdf("uqer/sec_map.h5","map") # sec_map 包含了约2800多个指数,实际指数约550只
history = pd.read_hdf("uqer/uq_history.h5","history") #hisotry 包含了从2004年到2017年11月16日的指数数据( 大约86万条数据).
#history = history.sort_index(level=0)
ntickers = history.index.levshape[0]
nTradeDate =history.index.levshape[1]/250
nRecords = history.shape[0]/10**4
print("交易历史数据库包含了:\n\t{1:,.0f}万条日交易数据.\n\t{0}只指数,\n\t单只指数最长交易记录为{2:.1f}年.".format(ntickers,nRecords,nTradeDate))
print("\n注 : 数据源基于Uqer,作了初步校对和修正,后存储在 History_fixed.h5 。例如:中证传媒2017年12月~1月的市盈率数据修正为choice的数据。\n\n")
print("历史交易数据:\n 特征列表:{0}".format(history.columns.tolist()))
print("股指名称数据:\n 特征列表:{0}".format(sec_map.columns.tolist()))
view_data()
map_E2C = {"ticker":"指数代码","secShortName":"指数名称",
'tradeDate':"日期", 'Close':"收盘价-Close",
'PB1':"市净率-PB", 'PE1':"市盈率-PE",
'TurnoverValue':"成交额", 'TurnoverVol':"成交量","ROE":"净资产回报率-ROE"}
print("\n本文使用的特征为:{0}".format(list(map_E2C.values())))
数据载入中... 交易历史数据库包含了: 91万条日交易数据. 550只指数, 单只指数最长交易记录为10.8年.
注 : 数据源基于Uqer,作了初步校对和修正,后存储在 History_fixed.h5 。例如:中证传媒2017年12月~1月的市盈率数据修正为choice的数据。
历史交易数据: 特征列表:['secID', 'Close', 'PB1', 'PB2', 'PE1', 'PE2', 'TurnoverValue', 'TurnoverVol'] 股指名称数据: 特征列表:['baseDate', 'basePoint', 'endDate', 'indexType', 'indexTypeCD', 'porgFullName', 'pubOrgCD', 'publishDate', 'secID', 'secShortName']
本文使用的特征为:['指数代码', '指数名称', '日期', '收盘价-Close', '市净率-PB', '市盈率-PE', '成交额', '成交量', '净资产回报率-ROE']
特征工程
1.2.1 筛选有效数据
数据中存在缺失,故只筛选截至2018年1月25日有交易记录的数据。
历史交易数据过少,没有统计意义(暂定至少3年)
def filter_history():
def ticker_filter(x):
ntradedays_annual = 250 # 假设一年交易日为250天
nyear=3 # 假设至少需要3年数据
checkday=Today # Checkday是设定有效的交易日期。默认为Today, 全局变量
mask_years = x.shape[0]>(ntradedays_annual*nyear)
mask_checkday = x.index.isin([checkday],level="tradeDate").any()
mask = mask_years & mask_checkday
return mask
history = pd.read_hdf("uqer/uq_history.h5","history") #hisotry 包含了从2004年到2017年11月16日的指数数据( 大约86万条数据).
history= history.loc(axis=0)[:,:Today]
history_filtered= history.groupby(level=0).filter(ticker_filter)
ntickers = len(history_filtered.groupby(level=0).groups)
print("{0}只指数交易时间超过了3年 且在{1}日有交易记录".format(ntickers,Today))
return history_filtered
history =filter_history()
483只指数交易时间超过了3年 且在2018-02-01日有交易记录
1.2.2 添加ROE(净资产回报率)特征
history["ROE"] = history["PB1"]/history["PE1"]
1.2.3 特征提取
交易日最新数据汇总。 取指定交易日因子数据
净资产回报率特征。 取一年的数据平均值,然后按回报率分成4个级别。级别(超低,低,中,高)
交易额规模特征。取一年的数据平均值,然后按日平均交易额分成4个级别(小于5亿,小于50亿,小于500亿,小于5000亿)
Z值(各个指标的标准差倍数)。 针对所有历史数据,计算Zscore(标准差倍数)。
def Check_summary():
def lastz(x):
freedom = 1 # it is sample, so the sample std degree of freedome should not be 0 but 1
Arry=x.values
zscore = stats.zmap(Arry[-1],Arry,ddof=freedom)
return zscore
def recent_mean(x):
mean = x.tail(250).sum()/250
return mean
grp = history.groupby(level=0)
grp_last = grp.agg({"Close":"last","PE1":"last","PB1":"last","ROE":"last","TurnoverValue":"last"})
grp_last["TurnoverValue"] =grp_last["TurnoverValue"]
grp_rank = grp.agg({"ROE":recent_mean,"TurnoverValue":recent_mean})
grp_z = grp.agg({"Close":lastz,"PE1":lastz,"PB1":lastz,"ROE":lastz,"TurnoverValue":lastz})
ROE_rank = pd.cut(grp_rank.ROE,bins=4,labels=["超低","低","中","高"])
TV_rank = pd.cut(grp_rank.TurnoverValue,bins=5*np.logspace(7,11,5),labels=["5亿","50亿","500亿","5000亿"])
ROE_rank.name = "净资产回报率等级"
TV_rank.name ="日交易额规模"
sec_map = pd.read_hdf("uqer/sec_map.h5","map") # sec_map 包含了约2800多个指数,实际指数约550只{}
#decimals = pd.Series([1,1,1,2,1 ], index=["Close","PE1","PB1","ROE","TurnoverValue"])
combined = sec_map[["secShortName"]].join(grp_last,how="right").join(ROE_rank,rsuffix="_R").join(TV_rank,rsuffix="_R")
combined = combined.join(grp_z,rsuffix="_Z")
return combined
checkday_summary = Check_summary()
checkday_summary.columns
Index(['secShortName', 'Close', 'PE1', 'PB1', 'ROE', 'TurnoverValue', '净资产回报率等级', '日交易额规模', 'CloseZ', 'PE1Z', 'PB1Z', 'ROEZ', 'TurnoverValue_Z'], dtype='object')
1.3 数据探索
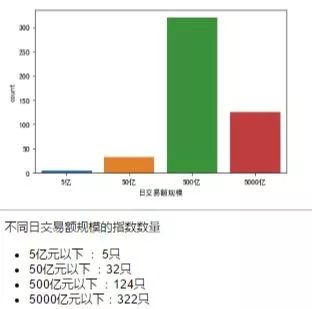
1.3.1 不同日交易额的指数群中指数的数量
tmp=sns.countplot('日交易额规模',data=checkday_summary)
checkday_summary.groupby(by="日交易额规模")[["ROE"]].mean().rename(columns={"ROE":"平均净资产回报率"})
1.3.2 收盘价(Close)
col="Close"
fig,ax = plt.subplots(1,2,figsize=(10,5))
sns.boxplot(x='日交易额规模',y=col,ax=ax[0],data=checkday_summary)
ax[0].set_title("不同规模指数 - {0}({1})箱体图".format(map_E2C[col],col))
sns.boxplot(x='日交易额规模',y=col+"_Z",ax=ax[1],data=checkday_summary)
ax[1].set_title("不同规模指数 - {0}({1})-Z值 箱体图".format(map_E2C[col],col))
指定日收盘价汇总箱形图 展现不同指数的收盘价差异: 左图是绝对值:不同规模的指数在该日收盘价价值不同。 右图是相对值:用Z值(即几个标准差)来衡量不同规模指数群的收盘价和各指数自己历史相比的差异。(500亿规模的指数收盘价差异比较大,Z指在4和-1之间。 从右图可以看出, 除了交易规模为50亿的小盘指数外,其他指数的日收盘价的Z值均值都在1附近。 各个日交易规模的指数群都有些Z值在(-1,1)之外的指数,这中间也许存在机会和风险。 Z值<-1, 有低估的可能。 可以考虑定投的方式逐步买入。 Z值>1, 有高估的可能。可以考虑逐步买出。
注:考虑到通货膨胀和指数内股票的增长,通常指数收盘价会出现Z值小于-1的情况。收盘价Z值>1甚至大于2都是比较常见的情况。
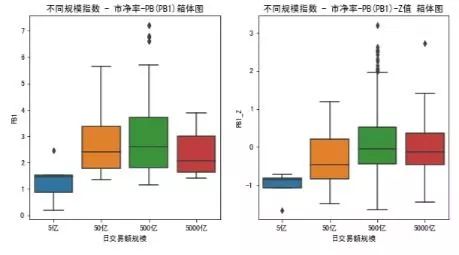
1.3.3 市盈率(PE1)
col="PE1"
fig,ax = plt.subplots(1,2,figsize=(10,5))
sns.boxplot(x='日交易额规模',y=col,ax=ax[0],data=checkday_summary)
ax[0].set_title("不同规模指数 - {0}({1})箱体图".format(map_E2C[col],col))
sns.boxplot(x='日交易额规模',y=col+"_Z",ax=ax[1],data=checkday_summary)
ax[1].set_title("不同规模指数 - {0}({1})-Z值 箱体图".format(map_E2C[col],col))
指定日市盈率汇总箱形图 展现不同指数的市盈率差异: 左图是绝对值:不同规模的指数在该日市盈率估值不同。 注:由于市盈率计算方法不一样,例如:加权,等权,算术平均等模式。故不同数据源的市盈率,市净率差异比较大。指数官网的市盈率和市净率比较权威。不过使用费用比较高。本文使用的是免费数据。因此可以看出这一天5亿规模指数群中有一个指数的市盈率小于-150倍。这是明显错误的。需要过滤掉。
右图是相关值:用Z值(即几个标准差)来衡量不同规模指数的市盈率和各自历史相比差异。 由于Z值计算是用全部历史数据来计算,故历史上的错误数据(如果数量不大的话,例如小于1%),对整理影响不大。只要将异常点过滤即可。 从右图可以看出,除了交易规模为50亿的小盘指数外,其他指数的日收盘价的Z值均值都在0附近。但是也有一些指数群中有(-1,1)之外的Z值。 Z值<-1, 有低估的可能。 可以考虑定投的方式逐步买入。 Z值>1, 有高估的可能。可以考虑逐步买出。 接下来,我们来看看都有哪些指数市盈率存在低估?
def show_min_PE_Z():
col="PE1"
def get_max(x):
colz= col+"_Z"
index =x[colz].idxmax()
return x.loc[index][["secShortName",col,colz]]
def get_min(x):
colz= col+"_Z"
index =x[colz].idxmin()
return x.loc[index][["secShortName",col,colz]]
print(checkday_summary.groupby("日交易额规模").apply(get_max).round(1))
print(checkday_summary.groupby("日交易额规模").apply(get_min).round(1))
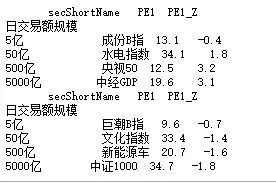
show_min_PE_Z()
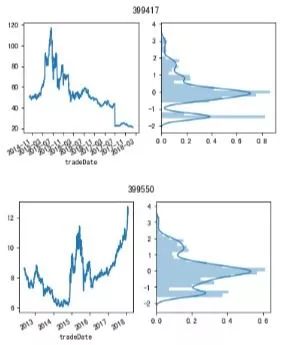
如上表中,所展示, 低估指数: Z值小于-1。 例如:中证1000(000852),新能源车(399417),文化指数分别是日交易规模(大盘,中盘,小盘)中Z值最低的指数。 高估指数:Z值大于2。 例如: 中经GDP,央视50(399550),水电指数分别是日交易规模(大盘,中盘,小盘)中Z值最高的指数。 如果这些指数的历史分布是正态, 那么根据经验法则,就存在较大的机会(针对低估)和风险(针对高估) 接下来,看看500亿日交易额规模指数群中新能源车和央视50这两个比较常见的指数历史数据的市盈率的波动。
tickers=["399417","399550"]
sec_map = pd.read_hdf("uqer/sec_map.h5","map")
for ticker in tickers:
print("{0} base day is {1}".format(ticker,sec_map.loc[ticker].baseDate))
fig,ax = plt.subplots(1,2,figsize=(6,3))
fig.suptitle(ticker)
PE1 = history.loc[ticker]["PE1"]
PE1_Z = history.loc[ticker][["PE1"]].apply(stats.zscore)
PE1.plot(ax=ax[0])
sns.distplot(PE1_Z,ax=ax[1],vertical=True)
从上图可以看出,2018年2月1日的市盈率图 新能源市盈率为22倍,绝对值不算高。但是Z指接近-1.5,相对值比较低,未来有很大的机会。 央视50市盈率为13倍,绝对值比较低。但是Z值接近4,相对值极度高,未来存在回归历史均值的风险
1.3.4 市净率 (PB1)
col="PB1"
fig,ax = plt.subplots(1,2,figsize=(10,5))
sns.boxplot(x='日交易额规模',y=col,ax=ax[0],data=checkday_summary)
ax[0].set_title("不同规模指数 - {0}({1})箱体图".format(map_E2C[col],col))
sns.boxplot(x='日交易额规模',y=col+"_Z",ax=ax[1],data=checkday_summary)
ax[1].set_title("不同规模指数 - {0}({1})-Z值 箱体图".format(map_E2C[col],col))
与市盈率数据类似 指定日市净率汇总箱形图 展现不同指数的市净率差异: 左图是绝对值:不同规模的指数在该日市净率估值不同。 右图是相关值:用Z值(即几个标准差)来衡量不同规模指数的市净率和各自历史相比差异。 从右图可以看出,除了交易规模为50亿的小盘指数外,其他指数的日收盘价的Z值均值都在0附近。但是也有一些指数群中有(-1,1)之外的Z值。 Z值<-1, 有低估的可能。 可以考虑定投的方式逐步买入。 Z值>1, 有高估的可能。可以考虑逐步买出。 接下来,我们来看看都有哪些指数市净率存在低估?
def show_min_PB_Z():
col="PB1"
def get_max(x):
colz= col+"_Z"
index =x[colz].idxmax()
return x.loc[index][["secShortName",col,colz]]
def get_min(x):
colz= col+"_Z"
index =x[colz].idxmin()
return x.loc[index][["secShortName",col,colz]]
print(checkday_summary.groupby("日交易额规模").apply(get_max).round(1))
print(checkday_summary.groupby("日交易额规模").apply(get_min).round(1))
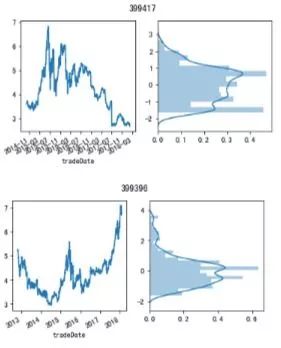
show_min_PB_Z()
从上图可以看出,2018年2月1日的市盈率图 新能源车市盈率为2.7倍,绝对值不算高。而且Z指接近-1.5,相对值比较低,未来有很大的机会。 国证食品市盈率为6.7倍,绝对值非常高。而且Z值接近3.2,相对值极度高,未来存在回归历史均值(3年历史)的风险。 注:由于国证食品指数在2004年就成立,缺少之前近十年历史数据。无法完全确定是否高估
1.3.5 净资产回报率(ROE)
col="ROE"
fig,ax = plt.subplots(1,2,figsize=(10,5))
sns.boxplot(x='日交易额规模',y=col,ax=ax[0],data=checkday_summary)
ax[0].set_title("不同规模指数 - {0}({1})箱体图".format(map_E2C[col],col))
sns.boxplot(x='日交易额规模',y=col+"_Z",ax=ax[1],data=checkday_summary)
ax[1].set_title("不同规模指数 - {0}({1})-Z值 箱体图".format(map_E2C[col],col))
与市盈率数据类似 指定日净资产回报率汇总箱形图 展现不同指数的净资产回报率差异: 左图是绝对值:不同规模的指数在该日净资产回报率估值不同。 右图是相关值:用Z值(即几个标准差)来衡量不同规模指数的净资产回报率和各自历史相比差异。 和市盈率与市净率不同,净资产回报率(ROE=PB/PE= profit/equity)排除了收盘价的短期波动影响,是比较长期的指标。我个人认为,长期指标稳健比较好。即ROE>0.1 而且Z指在(-1,1)之间的指数。
1.3.6 综合分析 - 流动性 + 风险 + 收益
前面已经单独对4个因子作了分析。他们分别代表了
流动性(日交易额规模),
风险(市盈率和市净率)
收益(净资产回报)
现在,让我们试着把这四个因子综合起来看看。
mask_scale= checkday_summary["日交易额规模"].isin(["50亿","500亿","5000亿"])
print("满足流动性规模的指数有{0}只".format(mask_scale.sum()))
risk_zscore= -1.4 #注 z值小于 -1 的 指数太少,故改设为-0.3
mask_risk= (checkday_summary["PE1_Z"]<0) & (checkday_summary["PB1_Z"]<0)\
&((checkday_summary["PE1_Z"] + checkday_summary["PB1_Z"]
print("满足低风险要求的指数有{0}只".format(mask_risk.sum()))
roe_score =["中","高"]
roe_zscore =[-2,2]
mask_roe = checkday_summary["净资产回报率等级"].isin(roe_score) & checkday_summary["ROE_Z"].between(roe_zscore[0],roe_zscore[-1])
print("满足收益率要求的指数有{0}只".format(mask_roe.sum()))
mask_all = mask_scale & mask_risk & mask_roe
result =checkday_summary[mask_all].drop_duplicates(subset=["secShortName"])
print("满足高流动性,低风险,较好收益率要求的指数有{0}只".format(result.shape[0]))
满足流动性规模的指数有478只 满足低风险要求的指数有59只 满足收益率要求的指数有310只 满足高流动性,低风险,较好收益率要求的指数有24只
投资策略
def strategy_tickers_today(strategy="customize",scale_score =None,risk_zscore =None,roe_score =None):
if strategy =="customize":
scale_score =["50亿","500亿","5000亿"]
scale_zscore=(-1,1)
risk_zscore= -1.4 #注 z值小于 -1 的 指数太少,故改设为-0.3
roe_score =["中","高"]
roe_zscore =[-2,2]
elif strategy =="ROE":
scale_score =None
risk_zscore= None
roe_score =["高"]
elif strategy =="RISK":
risk_zscore= -2 #PE & PB Z值小于-2, 如果是 正态分布,这风险小于95%
elif strategy =="TURNOVER":
scale_score =["5000亿"]
scale_zscore=(-1,1)
#交易规模过滤
if scale_score ==None:
mask_scale =True
else:
mask_scale= (checkday_summary["日交易额规模"].isin(scale_score)) \
& ( checkday_summary['TurnoverValue_Z'].between(scale_zscore[0],scale_zscore[-1]))
#风险指标过滤
if risk_zscore ==None:
mask_risk =True
else:
risk_zscore= -1.4
mask_risk= (checkday_summary["PE1_Z"]<0) & (checkday_summary["PB1_Z"]<0)\
&((checkday_summary["PE1_Z"] + checkday_summary["PB1_Z"]
#投资回报率过滤
if roe_score ==None:
mask_roe=True
else:
mask_roe = checkday_summary["净资产回报率等级"].isin(roe_score)
mask_all = mask_scale & mask_risk & mask_roe
result =checkday_summary[mask_all].drop_duplicates(subset=["secShortName"])
return result
def show_tickers_color(tickers= None):
if (tickers is None) or (tickers.shape[0]==0):
print("Pls prepare the checkday_summary dataframe")
return
else:
html =tickers[['secShortName','Close', 'PE1', 'PB1', 'ROE','Close_Z', 'PE1_Z', 'PB1_Z', 'ROE_Z','净资产回报率等级', '日交易额规模']]\
.round(2).rename(columns=map_E2C).style.bar(subset=['Close_Z', 'PE1_Z', 'PB1_Z'],\
align="zero", color=[ '#5fba7d','#d65f5f',],width=100/2)
return html
低风险策略
tmp = strategy_tickers_today("RISK")
tmp["RISK"] = tmp["PE1_Z"] + tmp["PB1_Z"]+tmp["Close_Z"]*0.2
show_tickers_color(tmp.sort_values(by=["ROE"],ascending=False).head(5))
根据不同的Z值组合和因子组合,高收益策略或者高容量策略也很容易合成。
衡量市场,指数高低是一个难题! 价值投资者很难判断,
现在是高估,还是低估?
买的是便宜还是,贵了?
应该现在买/卖,还是再等等?
针对这个问题,我在网上看到了一些量化的处理方法。例如:平均数法,中位数法,比例法等等。这种方法往往过于简单,只能衡量集中度。不能衡量离散度和概率。
也许统计方法中的标准差Z值法更加适合。既可以衡量某个指数的指标的集中度,还可以衡量离散度,和风险情况。尽管指数的数据也不是完美的正态分布,但Z值法依然存在较大参考意义。
我的观点:
Z值越大,越高估。因为大数定理认为:
Z>1, Z>2,意味着继续变大的可能性小于16%, 5%。Z值越小,越低估。
因为大数定理认为:Z<-1, Z<-2,意味着继续变小的可能性小于16%, 5%
综观550多只指数的历史数据。绝大部分指数的Z值都在-2,3之间。注:少数的能源,金属类指数曾经出现过短暂疯狂的。Z值法就不太适用。
我使用Python的Pandas 和 Matplotlib 等工具,加上一些渠道获得的指数数据(尤其是市盈率),发布热门指数Z值表。 今天又结合了不可能三角形思路做了一些投资策略的基本探索。
主要目的是:
方便自己定投使用。知道何时开始定投,何时停止定投,何时止盈。(目前还没有止盈过)
结合统计学,熟悉Python的基本数据分析方法。
网上分享给愿意参考的人,交流和学习
有不当之处,欢迎指正
本文作者
王勇,Python中文社区专栏作者,雪球ID:快乐_爸,目前感兴趣项目商业分析、Python、机器学习、Kaggle。17年项目管理,通信业干了11年项目经理管合同交付,制造业干了6年项目管理:PMO,变革,生产转移,清算和资产处理。MBA, PMI-PBA, PMP。
点击阅读原文加入CodingGo编程社区,
学习编程知识,收获互联网圈内人脉。