笔记(总结)-SVM(支持向量机)的理解-3

上篇讲述的Soft Margin SVM是为了解决线性不可分的问题，它解决问题的逻辑是通过允许一部分样本分得不那么准确（进入“楚河汉界”）甚至错分，使得在绝大多数样本能够正确地线性可分。本篇引入核函数(kernel)，从另一个思维角度来解决线性不可分问题。

问题引入

当样本在某个特征空间不可分时，可以通过将样本映射到另一个特征空间，在该空间中样本分布满足线性可分条件，再使用SVM进行学习分类：

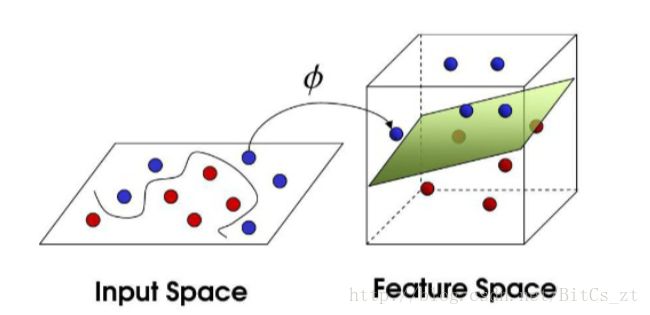
根据cover定理：将复杂模式分类问题非线性映射到高维空间比映射到低维空间更加可能线性可分。这直观上是很容易理解的，正如上图所示。

回到我们SVM的问题，对偶问题和判别函数为：

maxW(α)=∑iαi−12∑i∑jαiαjyiyjxTixj max W ( α ) = ∑ i α i − 1 2 ∑ i ∑ j α i α j y i y j x i T x j

s.t. ∑iαiyi=0, 0≤αi≤C s . t .   ∑ i α i y i = 0 ,   0 ≤ α i ≤ C

f(x)=wTx+b=(∑iαiyixTi)x+b=∑iαiyi(xTix)+b f ( x ) = w T x + b = ( ∑ i α i y i x i T ) x + b = ∑ i α i y i ( x i T x ) + b

将目标函数稍微变下形式 W(α)=∑iαi−12∑i∑jαiαjyiyj<xi,xj> W ( α ) = ∑ i α i − 1 2 ∑ i ∑ j α i α j y i y j < x i , x j > ，可以看到 W(α) W ( α ) 最终只和样本内积有关，同样的最终判别函数也只和内积有关。因此在SVM的计算过程中，我们从头到尾对样本的使用都是通过内积形式，建模开销基本上等同于内积运算的开销。

此时我们考虑在不同空间下内积的计算，当样本空间为 n n 维时，计算一次内积运算需要 n n 次乘法、 n−1 n − 1 次加法，时间开销为O(n)。在样本量较大的情况下，将样本从低维空间映射到高维空间，计算内积增加的开销是巨大的。有没有办法能降低这种开销呢？答案是核函数。

核函数(kernel)

给出核函数定义如下：

• 给定输入空间 X X 和映射空间 H H ，如果存在映射函数 ϕ ϕ 和函数 K K ，对于任意 x,z∈X x , z ∈ X ，满足 K(x,z)=<ϕ(x),ϕ(z)> K ( x , z ) =< ϕ ( x ) , ϕ ( z ) > ，则我们将 K K 称为核函数。

对于给定的核函数，映射空间和映射函数通常是不唯一的。举例如下：

X X 为2维空间， K(x,z)=<x,z>2 K ( x , z ) =< x , z > 2 ，取样本 x=(x1,x2) x = ( x 1 , x 2 ) 和 z=(z1,z2) z = ( z 1 , z 2 ) ，则有：

K(x,z)=<x,z>2=(x1z1+x2z2)2=(x1z1)2+2x1z1x2z2+(x2z2)2 K ( x , z ) =< x , z > 2 = ( x 1 z 1 + x 2 z 2 ) 2 = ( x 1 z 1 ) 2 + 2 x 1 z 1 x 2 z 2 + ( x 2 z 2 ) 2

当 H H 为3维空间时，取 ϕ(x)=(x21,2‾√x1x2,x22)T ϕ ( x ) = ( x 1 2 , 2 x 1 x 2 , x 2 2 ) T 、 ϕ(x)=12√((x1−x2)2,2x1x2,(x1+x2)2)T ϕ ( x ) = 1 2 ( ( x 1 − x 2 ) 2 , 2 x 1 x 2 , ( x 1 + x 2 ) 2 ) T 都能满足 K(x,z)=<ϕ(x),ϕ(z)> K ( x , z ) =< ϕ ( x ) , ϕ ( z ) > ；当 H H 为4维空间时，取 ϕ(x)=(x21,x1x2,x1x2,x22)T ϕ ( x ) = ( x 1 2 , x 1 x 2 , x 1 x 2 , x 2 2 ) T 也能满足要求。

当我们不使用核函数时，若 H H 为4维空间，直接计算 ϕ(x) ϕ ( x ) 的内积需要4次乘法和3次加法，而使用核函数只需要3次乘法，1次加法，计算次数显著下降。当 H H 为高维空间时，这种技巧能降低巨大的计算开销。

Kernel SVM

先将线性不可分情况下的样本映射到高维空间，得到对偶问题和判别函数：

maxW(α)=∑iαi−12∑i∑jαiαjyiyj<ϕ(xi),ϕ(xj)> max W ( α ) = ∑ i α i − 1 2 ∑ i ∑ j α i α j y i y j < ϕ ( x i ) , ϕ ( x j ) >

s.t. ∑iαiyi=0, 0≤αi≤C s . t .   ∑ i α i y i = 0 ,   0 ≤ α i ≤ C

f(x)=wTx+b=(∑iαiyixTi)x+b=∑iαiyi<ϕ(xi),ϕ(xj)>+b f ( x ) = w T x + b = ( ∑ i α i y i x i T ) x + b = ∑ i α i y i < ϕ ( x i ) , ϕ ( x j ) > + b

使用核函数转换，得到：

maxW(α)=∑iαi−12∑i∑jαiαjyiyjK(xi,xj) max W ( α ) = ∑ i α i − 1 2 ∑ i ∑ j α i α j y i y j K ( x i , x j )

s.t. ∑iαiyi=0, 0≤αi≤C s . t .   ∑ i α i y i = 0 ,   0 ≤ α i ≤ C

f(x)=wTx+b=(∑iαiyixTi)x+b=∑iαiyiK(xi,xj)+b f ( x ) = w T x + b = ( ∑ i α i y i x i T ) x + b = ∑ i α i y i K ( x i , x j ) + b

不论最后 ϕ ϕ 函数映射后的特征空间维度多高，SVM的求解都在原样本空间内用核函数进行。

常用的核

由上所述，选择不同的核函数实际上对应的是不同的映射方式。介绍几种常用的核函数。

线性核

即SVM中最基本的 <xi,xj> < x i , x j > ，不进行任何映射变换。在样本线性可分情况下（实际中一般通过训练Linear SVM观察拟合效果来判断是否线性可分），线性核运算开销小，通常能达到比较好的效果。

多项式核

多项式核定义如下：

K(x,z)=(αxTz+β)p K ( x , z ) = ( α x T z + β ) p

多项式核实际中应用比较少，在线性可分情况下性能不如线性核，在线性不可分情况下效果不如高斯核。

高斯核

高斯核(Gaussian Kernel)也称radial basis function(RBF) kernel，定义如下：

K(x,z)=exp(−||x−z||22σ2) K ( x , z ) = exp ⁡ ( − | | x − z | | 2 2 σ 2 )

高斯核是最强大、应用最广泛的核函数。线性不可分情况下能展现出强大的分类能力，但是开销较大。为何说高斯核最强大，因为高斯核可以看做“无穷度数的正则化多项式核”。首先将指数函数进行泰勒展开：

exp(xTz)=∑∞0(xTz)ii! e x p ( x T z ) = ∑ 0 ∞ ( x T z ) i i !

只写出展开式前几项，看得更清晰：

exp(xTz)=1+xTz+(xTz)22!+(xTz)33!+... e x p ( x T z ) = 1 + x T z + ( x T z ) 2 2 ! + ( x T z ) 3 3 ! + . . .

与多项式核定义对比，每一项几乎都是最简化版的多项式核。再考虑将上述指数函数进行正则化：

exp(xTz)exp(xTx)√exp(zTz)√=exp[−12(xTx+zTz−2xTz)]=exp(−||x−z||22) e x p ( x T z ) e x p ( x T x ) e x p ( z T z ) = e x p [ − 1 2 ( x T x + z T z − 2 x T z ) ] = e x p ( − | | x − z | | 2 2 )

可以看到我们几乎得到了高斯核，由此可以论证高斯核是“无穷度数的正则化多项式核”，它实际上考虑了常数项、一次项、二次项…一直到无穷多次项，功能强大之处一目了然。

在实际中，具体使用哪种核一是靠经验分析，二是试错调参。在具体应用中，分析数据进行尝试，再通过模型结果反过来理解数据，没有捷径可走。对核有一定的了解能让调参变得更有迹可循。

本文先阐述了核函数的引入来由，具体讲述了核函数的定义和SVM中如何应用核函数来降低计算量，最后列举了SVM中常用的几种核函数并给出解释。