周志华《机器学习》(西瓜书) —— 学习笔记:第6章 支持向量机
文章目录
- 6.0 学习导图
- 6.1 基本流程
- 6.2 对偶问题
- 6.3 核函数
- 6.4 软间隔与正则化
- 6.5 支持向量回归
- 6.6 核方法
6.0 学习导图
6.1 基本流程
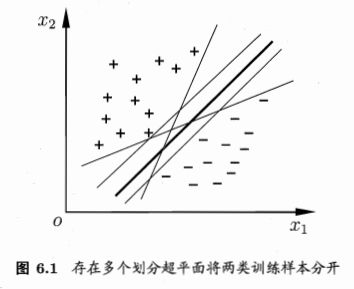
给定训练样本集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } , y i ∈ { − 1 , + 1 } D=\left\{\left(\boldsymbol{x}_{1}, y_{1}\right),\left(\boldsymbol{x}_{2}, y_{2}\right), \ldots,\left(\boldsymbol{x}_{m}, y_{m}\right)\right\},y_{i} \in\{-1,+1\} D={(x1,y1),(x2,y2),…,(xm,ym)},yi∈{−1,+1} ,在样本空间中找到一个超平面,将不同类别的样本分开。
在样本空间中,划分超平面可通过如下线性方程描述:
(6.1) w T x + b = 0 \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b=0\tag{6.1} wTx+b=0(6.1)
其中 w = ( w 1 w 2 ⋮ w d ) \boldsymbol{w}=\left( \begin{array}{c}{w_{1}} \\ {w_{2}} \\ {\vdots} \\ {w_{d}}\end{array}\right) w=⎝⎜⎜⎜⎛w1w2⋮wd⎠⎟⎟⎟⎞ 为法向量,决定超平面的方向, b b b 为位移项,决定超平面与原点之间的距离。将超平面简写为 ( w , b ) (\boldsymbol{w}, b) (w,b) 。样本空间中任意点 x \boldsymbol{x} x 到超平面 ( w , b ) (\boldsymbol{w}, b) (w,b) 的距离为
(6.2) r = ∣ w T x + b ∣ ∥ w ∥ r=\frac{\left|\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\right|}{\|\boldsymbol{w}\|}\tag{6.2} r=∥w∥∣∣wTx+b∣∣(6.2)
证:从点 x \boldsymbol{x} x 向超平面 ( w , b ) (\boldsymbol{w}, b) (w,b) 做垂线,垂足为 x 0 \boldsymbol{x_0} x0 ,令 r = x − x 0 \boldsymbol{r}=\boldsymbol{x}-\boldsymbol{x_0} r=x−x0 ,则 r = ∥ x − x 0 ∥ r=\|\boldsymbol{x}-\boldsymbol{x_0}\| r=∥x−x0∥ ,显然, w \boldsymbol{w} w 平行于 r \boldsymbol{r} r ,故有
∣ w T ( x − x 0 ) ∣ = ∣ w T r ∣ = ∣ w ⋅ r ∣ = ∥ w ∥ ∥ r ∥ = ∥ w ∥ r |\boldsymbol{w}^\mathrm{T}(\boldsymbol{x}-\boldsymbol{x_0})|=|\boldsymbol{w}^\mathrm{T}\boldsymbol{r}|=|\boldsymbol{w}\cdot\boldsymbol{r}|=\|\boldsymbol{w}\|\|\boldsymbol{r}\|=\|\boldsymbol{w}\|r ∣wT(x−x0)∣=∣wTr∣=∣w⋅r∣=∥w∥∥r∥=∥w∥r
又 x 0 \boldsymbol{x_0} x0 在超平面上,故有
w T x 0 + b = 0 \boldsymbol{w}^{\mathrm{T}}\boldsymbol{x_0}+b=0 wTx0+b=0
所以
∣ w T ( x − x 0 ) ∣ = ∣ w T x − w T x 0 ∣ = ∣ w T x + b ∣ |\boldsymbol{w}^\mathrm{T}(\boldsymbol{x}-\boldsymbol{x_0})|=|\boldsymbol{w}^\mathrm{T}\boldsymbol{x}-\boldsymbol{w}^\mathrm{T}\boldsymbol{x_0}|=|\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b| ∣wT(x−x0)∣=∣wTx−wTx0∣=∣wTx+b∣
联立,可得式(6.2)
假设超平面 ( w , b ) (\boldsymbol{w},b) (w,b) 能将训练样本正确分类,即有
{ w T x i + b > 0 , y i = + 1 w T x i + b < 0 , y i = − 1 \left\{\begin{array}{ll}{\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b > 0,} & {y_{i}=+1} \\ {\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b < 0,} & {y_{i}=-1}\end{array}\right. {wTxi+b>0,wTxi+b<0,yi=+1yi=−1
则对 w \boldsymbol{w} w 和 b b b 进行等比例缩放,一定能有
(6.3) { w T x i + b ⩾ + 1 , y i = + 1 w T x i + b ⩽ − 1 , y i = − 1 \left\{\begin{array}{ll}{\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b \geqslant+1,} & {y_{i}=+1} \\ {\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b \leqslant-1,} & {y_{i}=-1}\end{array}\right.\tag{6.3} {wTxi+b⩾+1,wTxi+b⩽−1,yi=+1yi=−1(6.3)
如图 6.2 所示,距离超平面最近的几个训练样本使式(6.3)的等号成立,它们被称为“支持向量”,两个异类支持向量到超平面的距离之和为
(6.4) γ = 2 ∥ w ∥ \gamma=\frac{2}{\|\boldsymbol{w}\|}\tag{6.4} γ=∥w∥2(6.4)
它被称为“间隔”。
要找到具有“最大化间隔”的划分超平面,也就是要找到能满足式(6.3)中约束的参数 w \boldsymbol{w} w 和 b b b ,使得 γ \gamma γ 最大,即
(6.5) max w , b 2 ∥ w ∥ s.t. y i ( w T x i + b ) ⩾ 1 , i = 1 , 2 , … , m \begin{array}{l}{\max _{w, b} \frac{2}{\|\boldsymbol{w}\|}} \\\\ {\text { s.t. } y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right) \geqslant 1, \quad i=1,2, \ldots, m}\end{array}\tag{6.5} maxw,b∥w∥2 s.t. yi(wTxi+b)⩾1,i=1,2,…,m(6.5)
显然,上式(6.5)与下式(6.6)等价
(6.6) min w , b 1 2 ∥ w ∥ 2 s.t. y i ( w T x i + b ) ⩾ 1 , i = 1 , 2 , … , m \begin{array}{l}{\min _{\boldsymbol{w}, b} \frac{1}{2}\|\boldsymbol{w}\|^{2}} \\\\ {\text { s.t. } y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right) \geqslant 1, \quad i=1,2, \ldots, m}\end{array}\tag{6.6} minw,b21∥w∥2 s.t. yi(wTxi+b)⩾1,i=1,2,…,m(6.6)
这就是支持向量机(简称SVM)的基本型。
6.2 对偶问题
求解式(6.6)可得到最大间隔划分超平面所对应的模型
(6.7) f ( x ) = w T x + b f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\tag{6.7} f(x)=wTx+b(6.7)
其中 w \boldsymbol{w} w 和 b b b 是模型参数。
式(6.6)是一个凸二次规划,可以利用拉格朗日乘子法得到其“对偶问题”:
- 将式(6.6)写成如下形式
(6.6) min w , b 1 2 ∥ w ∥ 2 s.t. 1 − y i ( w T x i + b ) ⩽ 0 , i = 1 , 2 , … , m \begin{array}{l}{\min _{\boldsymbol{w}, b} \frac{1}{2}\|\boldsymbol{w}\|^{2}} \\\\ {\text { s.t. } 1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right) \leqslant 0, \quad i=1,2, \ldots, m}\end{array}\tag{6.6} minw,b21∥w∥2 s.t. 1−yi(wTxi+b)⩽0,i=1,2,…,m(6.6)
- 引入拉格朗日乘子 α i ⩾ 0 \alpha_i\geqslant0 αi⩾0 ,得到其拉格朗日函数
(6.8) L ( w , b , α ) = 1 2 ∥ w ∥ 2 + ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) , 其 中 , α = ( α 1 α 2 ⋮ α m ) L(\boldsymbol{w}, b, \boldsymbol{\alpha})=\frac{1}{2}\|\boldsymbol{w}\|^{2}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)\right),其中,\boldsymbol{\alpha}=\left( \begin{array}{c}{\alpha_{1}} \\ {\alpha_{2}} \\ {\vdots} \\ {\alpha_{m}}\end{array}\right)\tag{6.8} L(w,b,α)=21∥w∥2+i=1∑mαi(1−yi(wTxi+b)),其中,α=⎝⎜⎜⎜⎛α1α2⋮αm⎠⎟⎟⎟⎞(6.8)
- 显然
1 2 ∥ w ∥ 2 = max α ≽ 0 L ( w , b , α ) \frac{1}{2}\|\boldsymbol{w}\|^{2}=\max _{\boldsymbol{\alpha}\succcurlyeq0} L(\boldsymbol{w}, b, \boldsymbol{\alpha}) 21∥w∥2=α≽0maxL(w,b,α)
- 原问题转化为
min w , b max α ≽ 0 L ( w , b , α ) \min _{\boldsymbol{w}, b} \max _{\boldsymbol{\alpha}\succcurlyeq0} L(\boldsymbol{w}, b, \boldsymbol{\alpha}) w,bminα≽0maxL(w,b,α)
- 其对偶问题为
max α ≽ 0 min w , b L ( w , b , α ) \max _{\boldsymbol{\alpha}\succcurlyeq0} \min _{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \boldsymbol{\alpha}) α≽0maxw,bminL(w,b,α)
- 对 w \boldsymbol{w} w 和 b b b 求偏导令其为 0 0 0,得到内层取最小值时的解
(6.9) w = ∑ i = 1 m α i y i x i \boldsymbol{w}=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i}\tag{6.9} w=i=1∑mαiyixi(6.9)
(6.10) 0 = ∑ i = 1 m α i y i 0=\sum_{i=1}^{m} \alpha_{i} y_{i}\tag{6.10} 0=i=1∑mαiyi(6.10)
- 代回式(6.8)
L ( w , b , α ) = 1 2 ∥ w ∥ 2 + ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) = 1 2 w T w + ∑ i = 1 m α i − ∑ i = 1 m α i y i w T x i − b ∑ i = 1 m α i y i = 1 2 ∑ i = 1 m α i y i x i T ∑ i = 1 m α i y i x i + ∑ i = 1 m α i − ∑ i = 1 m α i y i ( ∑ i = 1 m α i y i x i T ) x i − 0 = ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j \begin{aligned} L(\boldsymbol{w}, b, \boldsymbol{\alpha})&=\frac{1}{2}\|\boldsymbol{w}\|^{2}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)\right) \\ &=\frac{1}{2}\boldsymbol{w}^\mathrm{T}\boldsymbol{w}+\sum_{i=1}^{m} \alpha_{i}-\sum_{i=1}^{m} \alpha_{i}y_{i}\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}-b\sum_{i=1}^{m} \alpha_{i}y_{i} \\ &=\frac{1}{2}\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i}^\mathrm{T}\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i}+\sum_{i=1}^{m} \alpha_{i}-\sum_{i=1}^{m} \alpha_{i}y_{i}(\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i}^\mathrm{T})\boldsymbol{x}_{i}-0 \\ &=\sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{x}_{j} \end{aligned} L(w,b,α)=21∥w∥2+i=1∑mαi(1−yi(wTxi+b))=21wTw+i=1∑mαi−i=1∑mαiyiwTxi−bi=1∑mαiyi=21i=1∑mαiyixiTi=1∑mαiyixi+i=1∑mαi−i=1∑mαiyi(i=1∑mαiyixiT)xi−0=i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj
- 加上约束条件,得到原问题的对偶问题
(6.11) max α ( ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j ) s.t. ∑ i = 1 m α i y i = 0 α i ⩾ 0 , i = 1 , 2 , … , m \begin{aligned}&{\max _{\alpha} (\sum_{i=1}^{m} \alpha_{i}- \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{x}_{j}}) \\\\ &\text { s.t. } {\sum_{i=1}^{m} \alpha_{i} y_{i}=0} \\\\ &\ \ \ \ \ \ \ {\alpha_{i} \geqslant 0, \quad i=1,2, \ldots, m}\end{aligned}\tag{6.11} αmax(i=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxj) s.t. i=1∑mαiyi=0 αi⩾0,i=1,2,…,m(6.11)
令 α ∗ \boldsymbol\alpha^* α∗ 是式(6.11)的解,则可得到 w \boldsymbol{w} w 和 b b b 进而得到模型
(6.12) f ( x ) = w T x + b = ∑ i = 1 m α i y i x i T x + b \begin{aligned} f(\boldsymbol{x}) &=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b \\ &=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i}^{\mathrm{T}} \boldsymbol{x}+b \end{aligned}\tag{6.12} f(x)=wTx+b=i=1∑mαiyixiTx+b(6.12)
一般情况下, max α ≽ 0 min w , b L ( w , b , α ) ⩽ min w , b max α ≽ 0 L ( w , b , α ) \max _{\boldsymbol{\alpha}\succcurlyeq0} \min _{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \boldsymbol{\alpha})\leqslant\min _{\boldsymbol{w}, b} \max _{\boldsymbol{\alpha}\succcurlyeq0} L(\boldsymbol{w}, b, \boldsymbol{\alpha}) maxα≽0minw,bL(w,b,α)⩽minw,bmaxα≽0L(w,b,α) ,即对偶问题的函数值小于等于原问题的函数值,若要两者相等,需要函数满足 KKT 条件
(6.13) { α i ⩾ 0 y i f ( x i ) − 1 ⩾ 0 α i ( y i f ( x i ) − 1 ) = 0 \left\{\begin{array}{l}{\alpha_{i} \geqslant 0} \\\\ {y_{i} f\left(\boldsymbol{x}_{i}\right)-1 \geqslant 0} \\\\ {\alpha_{i}\left(y_{i} f\left(\boldsymbol{x}_{i}\right)-1\right)=0}\end{array}\right.\tag{6.13} ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧αi⩾0yif(xi)−1⩾0αi(yif(xi)−1)=0(6.13)
注:对于拉格朗日乘子法的学习和理解整理在《周志华《机器学习》(西瓜书) ——相关数学知识整理:拉格朗日乘子法与 KKT 条件》中。
解 α ∗ \boldsymbol\alpha^* α∗ 常用 SMO 方法
6.3 核函数
将式(6.7)中的 x \boldsymbol{x} x 用 ϕ ( x ) \phi(\boldsymbol{x}) ϕ(x) 代替,常用于将原始输入空间映射到新的高维特征空间,使原本线性不可分的样本在核空间可分。
6.4 软间隔与正则化
所有样本都必须划分正确“硬间隔”,允许一些错误“软间隔”。引入损失函数和松弛变量。
软间隔增强泛化能力,可防止过拟合,但容易产生欠拟合。
6.5 支持向量回归
将分类模型转化成回归模型:SVR 支持向量回归
6.6 核方法
基于核函数的一系列学习方法:“核方法”