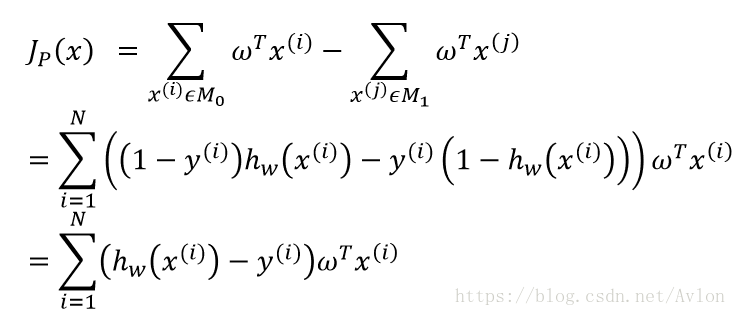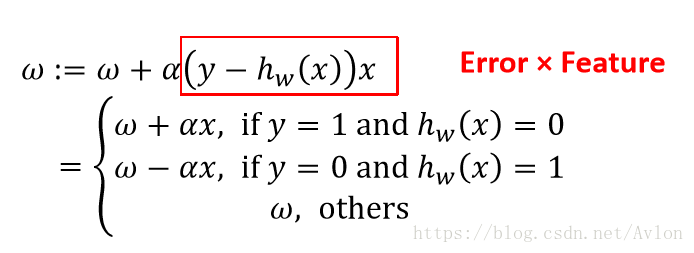机器学习笔记 perceptron(感知机) 在ex4Data数据集上的实现
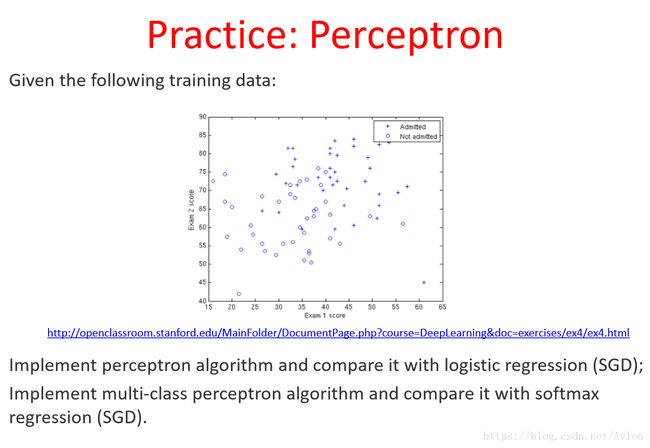
惯例的ML课堂作业,第四个也是最后一个线性分类模型,感知机。
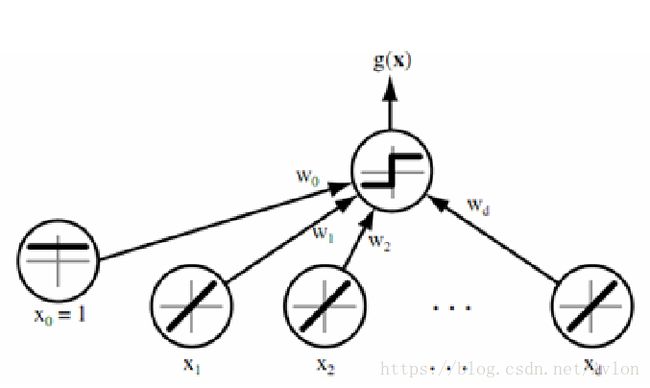
感知机是一个非常简单的线性分类模型,简单来说就是一个神经元,其激活函数是门限函数,有n个输入和一个输出,和神经元结构十分相似。
感知机的损失函数是看作是分类错的所有样本的输出值的和
hw的输出就是模型的预测结果,对于二分类问题就是0/1两种,y是真实标记。当预测和真实一致时,求和项为0,当hw取1,真实样本为0,系数为1。hw输入正值时才预测1所以整一项也是取正值,相反时系数为-1,但是输入值也是负数,最后还是正数。
损失函数形式很简单,对参数求导就可以得到梯度值。
对于SGD优化,参数更新规则如下:
由于数据是线性不可分的,SGD下会不断的震荡,用GD的话可以稳定结果,但是参数会不断扩大直到超出表示范围。GD就是把所有的SGD更新加起来而已。
下面给出代码:
import numpy as np
import matplotlib.pyplot as plt
import random
data_x = np.loadtxt("ex4Data/ex4x.dat")
data_y = np.loadtxt("ex4Data/ex4y.dat")
data_x_plt = data_x
plt.axis([15, 65, 40, 90])
plt.xlabel("exam 1 score")
plt.ylabel("exam 2 score")
for i in range(data_y.size):
if data_y[i] == 1:
plt.plot(data_x[i][0], data_x[i][1], 'b+')
else:
plt.plot(data_x[i][0], data_x[i][1], 'bo')
mean = data_x.mean(axis=0)
variance = data_x.std(axis=0)
data_x = (data_x-mean)/variance
data_y = data_y.reshape(-1, 1) # 拼接
temp = np.ones(data_y.size)
data_x = np.c_[temp, data_x]
data_x = np.mat(data_x)
learn_rate = 1
theda = np.mat(np.zeros([3, 1]))
loss = np.sum(np.multiply(np.heaviside(data_x*theda, 1)-data_y, (data_x*theda)))
old_loss = 0
# plt.ion()
for i in range(1000):
z = random.randint(0, data_y.size-1)
if int(data_y[z]) == 0 and int(np.sum(data_x[z]*theda)) == 1:
theda = theda-learn_rate*data_x[z].T
if int(data_y[z]) == 1 and int(np.sum(data_x[z]*theda)) == 0:
theda = theda+learn_rate*data_x[z].T
# print(np.sum(np.multiply(np.heaviside(data_x*theda, 1)-data_y, (data_x*theda))))
# plt.cla()
# plt.axis([15, 65, 40, 90])
# plt.xlabel("exam 1 score")
# plt.ylabel("exam 2 score")
# for j in range(data_y.size):
# if data_y[j] == 1:
# plt.plot(data_x_plt[j][0], data_x_plt[j][1], 'b+')
# else:
# plt.plot(data_x_plt[j][0], data_x_plt[j][1], 'bo')
# theta = np.array(theda)
# plot_y = np.zeros(65 - 16)
# plot_x = np.arange(16, 65)
# for i in range(16, 65):
# plot_y[i - 16] = -(theta[0] + theta[2] * ((i - mean[0]) / variance[0])) / theta[1]
# plot_y[i - 16] = plot_y[i - 16] * variance[1] + mean[1]
# plt.plot(plot_x, plot_y)
# plt.pause(0.1)
theta = np.array(theda)
plot_y = np.zeros(65-16)
plot_x = np.arange(16, 65)
for i in range(16, 65):
plot_y[i - 16] = -(theta[0] + theta[2] * ((i - mean[0]) / variance[0])) / theta[1]
plot_y[i - 16] = plot_y[i - 16] * variance[1] + mean[1]
plt.plot(plot_x, plot_y)
plt.show()注释掉的一部分代码是实时显示线性分类结果的,可以看到分类器是如何一步一步更新到最佳位置附近,因为会经常抽到分类正确的样本,所以很多时候模型并不更新参数,这里可以简单优化一下让模型只在分类错误的样本中随机抽取,不过我犯懒了
下面给出GD算法下的代码:
import numpy as np
import matplotlib.pyplot as plt
import random
data_x = np.loadtxt("ex4Data/ex4x.dat")
data_y = np.loadtxt("ex4Data/ex4y.dat")
data_x_plt = data_x
plt.axis([15, 65, 40, 90])
plt.xlabel("exam 1 score")
plt.ylabel("exam 2 score")
for i in range(data_y.size):
if data_y[i] == 1:
plt.plot(data_x[i][0], data_x[i][1], 'b+')
else:
plt.plot(data_x[i][0], data_x[i][1], 'bo')
mean = data_x.mean(axis=0)
variance = data_x.std(axis=0)
data_x = (data_x-mean)/variance
data_y = data_y.reshape(-1, 1) # 拼接
temp = np.ones(data_y.size)
data_x = np.c_[temp, data_x]
data_x = np.mat(data_x)
learn_rate = 0.18
theda = np.mat(np.zeros([3, 1]))
loss = np.sum(np.multiply(np.heaviside(data_x*theda, 1)-data_y, (data_x*theda)))
old_loss = 0
# plt.ion()
for i in range(100):
temp = np.mat(np.zeros([3, 1]))
inference = data_x*theda
for j in range(data_y.size):
temp += learn_rate*(float(data_y[j])-float(np.sum(inference[j])))*data_x[j].T
theda += temp
# print(np.sum(np.multiply(np.heaviside(data_x*theda, 1)-data_y, (data_x*theda))))
# plt.cla()
# plt.axis([15, 65, 40, 90])
# plt.xlabel("exam 1 score")
# plt.ylabel("exam 2 score")
# for j in range(data_y.size):
# if data_y[j] == 1:
# plt.plot(data_x_plt[j][0], data_x_plt[j][1], 'b+')
# else:
# plt.plot(data_x_plt[j][0], data_x_plt[j][1], 'bo')
# theta = np.array(theda)
# plot_y = np.zeros(65 - 16)
# plot_x = np.arange(16, 65)
# for i in range(16, 65):
# plot_y[i - 16] = -(theta[0] + theta[2] * ((i - mean[0]) / variance[0])) / theta[1]
# plot_y[i - 16] = plot_y[i - 16] * variance[1] + mean[1]
# plt.plot(plot_x, plot_y)
# plt.pause(0.1)
theta = np.array(theda)
plot_y = np.zeros(65-16)
plot_x = np.arange(16, 65)
for i in range(16, 65):
plot_y[i - 16] = -(theta[0] + theta[2] * ((i - mean[0]) / variance[0])) / theta[1]
plot_y[i - 16] = plot_y[i - 16] * variance[1] + mean[1]
plt.plot(plot_x, plot_y)
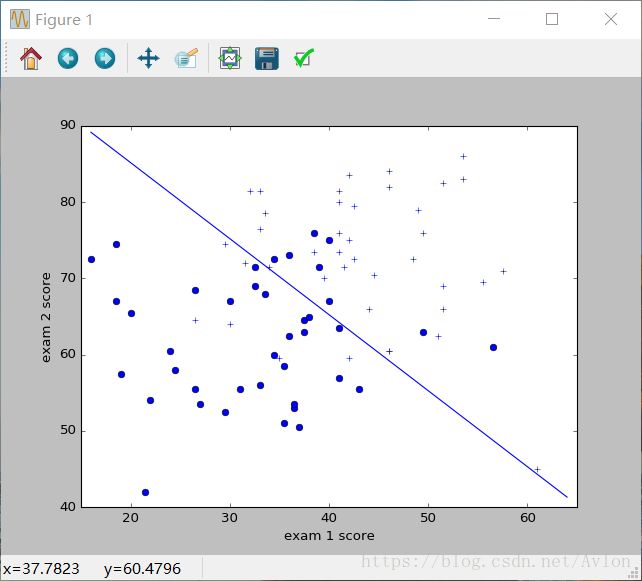
plt.show()注释掉的部分一样是实时划线用的,跟前文说的一样其参数在稳定后会不断的正比例增长,所以loss值也是不断增大,直到超出表示范围。
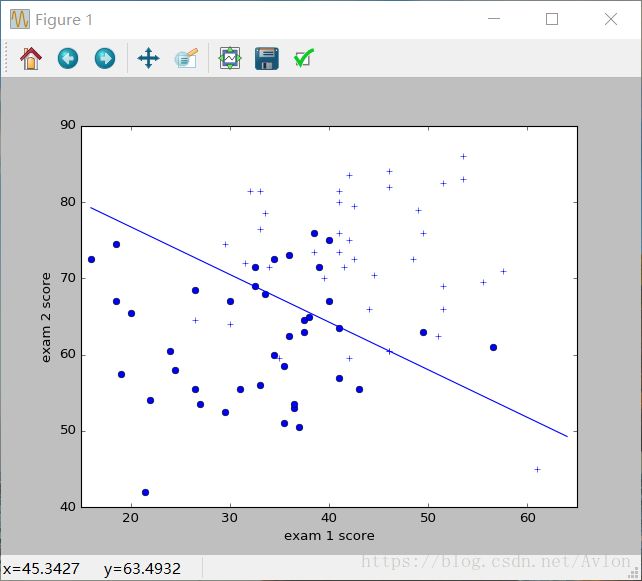
结果图
第二个是多分类的感知机,有几类需要分类的数据就有几个神经元输出,选其中值最大的为正确类别,取消了阶跃函数。其他基本跟二分类一样。
最后结果需要画出两条线,不过因为是二分类所以画的线不会有多少偏差。
首先是代码,这次的SGD一次抽取2个样本,模型的震荡变得更小。
import numpy as np
import matplotlib.pyplot as plt
import random
data_x = np.loadtxt("ex4Data/ex4x.dat")
data_y = np.loadtxt("ex4Data/ex4y.dat")
plt.axis([15, 65, 40, 90])
plt.xlabel("exam 1 score")
plt.ylabel("exam 2 score")
for i in range(data_y.size):
if data_y[i] == 1:
plt.plot(data_x[i][0], data_x[i][1], 'b+')
else:
plt.plot(data_x[i][0], data_x[i][1], 'bo')
mean = data_x.mean(axis=0)
variance = data_x.std(axis=0)
data_x = (data_x-mean)/variance
data_y = data_y.reshape(-1, 1) # 拼接
temp = np.ones(data_y.size)
data_x = np.c_[temp, data_x]
data_x = np.mat(data_x)
learn_rate = 0.1
theda = np.mat(np.zeros([3, 2]))
loss = np.sum(np.max(data_x*theda)-data_x*theda)
for i in range(3000):
temp = theda.T
for s in range(2):
z = random.randint(0, data_y.size - 1)
for j in range(2):
if j == np.argmax(data_x[z]*theda) and j != int(data_y[z]):
temp[j] -= learn_rate*data_x[z]
if j != np.argmax(data_x[z]*theda) and j == int(data_y[z]):
temp[j] += learn_rate*data_x[z]
theda = temp.T
# print(np.sum(np.max(data_x*theda)-data_x*theda))
theta = np.array(theda)
plot_y = np.zeros(65-16)
plot_x = np.arange(16, 65)
for i in range(16, 65):
plot_y[i - 16] = -(theta[0][0] + theta[2][0] * ((i - mean[0]) / variance[0])) / theta[1][0]
plot_y[i - 16] = plot_y[i - 16] * variance[1] + mean[1]
plt.plot(plot_x, plot_y)
for i in range(16, 65):
plot_y[i - 16] = -(theta[0][1] + theta[2][1] * ((i - mean[0]) / variance[0])) / theta[1][1]
plot_y[i - 16] = plot_y[i - 16] * variance[1] + mean[1]
plt.plot(plot_x, plot_y)
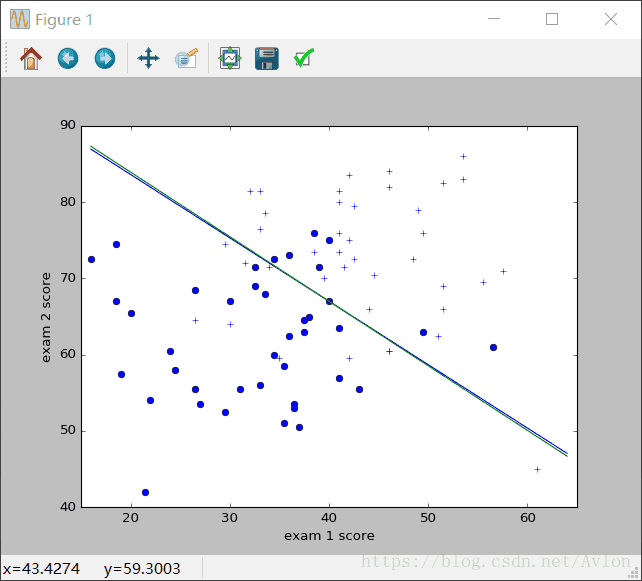
plt.show()结果如图:
收敛应该不需要这么多步,不过我也是犯懒了,而且说实话这个数据集真是有点用腻了……
有其他优化和想法的话会再更新