基于随机森林的特征选择算法
http://xuebao.jlu.edu.cn/gxb/article/2014/1671-5497-44-1-137.html
图像处理、信息检索以及生物信息学等技术的发展,产生了以超大规模特征为特点的高维数据集。如何有效地从高维数据中提取或选择出有用的特征信息或规律,并将其分类识别已成为当今信息科学与技术所面临的基本问题[ 1]。特征选择是指从原始特征集中选择使某种评估标准最优的特征子集,以使在该最优特征子集上所构建的分类或回归模型达到与特征选择前近似甚至更好的预测精度。Davies证明寻找满足要求的最小特征子集是NP完全问题[ 2]。在实际应用中,通常是通过采用启发式搜索算法,在运算效率和特征子集质量间找到一个好的平衡点,即近似最优解。
随机森林(Random forest,RF)[ 3]是一种集成机器学习方法,它利用随机重采样技术bootstrap和节点随机分裂技术构建多棵决策树,通过投票得到最终分类结果。RF具有分析复杂相互作用分类特征的能力,对于噪声数据和存在缺失值的数据具有很好的鲁棒性,并且具有较快的学习速度,其变量重要性度量可以作为高维数据的特征选择工具,近年来已经被广泛应用于各种分类、预测、特征选择以及异常点检测问题中[ 4, 5, 6, 7]。
特征选择算法根据所采用的特征评价策略可以分为Filter和Wrapper两大类[ 8]。Filter方法独立于后续采取的机器学习算法,可以较快地排除一部分非关键性的噪声特征,缩小优化特征子集搜索范围,但它并不能保证选择出一个规模较小的优化特征子集。Wrapper方法在筛选特征的过程中直接用所选特征子集来训练分类器,根据分类器在测试集的性能表现来评价该特征子集的优劣,该方法在计算效率上不如Filter方法,但其所选的优化特征子集的规模相对要小一些。
本文以随机森林算法为基本工具研究Wrapper特征选择方法,利用随机森林分类器的分类准确率作为特征可分性判据,基于随机森林算法本身的变量重要性度量进行特征重要性排序,利用序列后向选择方法(Sequential backward selection,SBS)和广义序列后向选择方法(Generalized sequential backward selection,GSBS)选取特征子集。实验结果表明,相比于文献中[9-10]已有的特征选择算法,本文的算法在性能上有较大的提高。
定义1 随机森林[ 3]是一个由一组决策树分类器{ h( X, θ k), k=1,2,…, K}组成的集成分类器,其中{ θ k}是服从独立同分布的随机向量,K表示随机森林中决策树的个数,在给定自变量 X下,每个决策树分类器通过投票来决定最优的分类结果。
随机森林是许多决策树集成在一起的分类器,如果把决策树看成分类任务中的一个专家,随机森林就是许多专家在一起对某种任务进行分类。
生成随机森林的步骤如下:
(1)从原始训练数据集中,应用bootstrap方法有放回地随机抽取 K个新的自助样本集,并由此构建 K棵分类回归树,每次未被抽到的样本组成了 K个袋外数据(Out-of-bag,OOB)。
(2)设有 n个特征,则在每一棵树的每个节点处随机抽取 m try 个特征( m try≤ n),通过计算每个特征蕴含的信息量,在 m try个特征中选择一个最具有分类能力的特征进行节点分裂。
(3)每棵树最大限度地生长,不做任何剪裁。
(4)将生成的多棵树组成随机森林,用随机森林对新的数据进行分类,分类结果按树分类器的投票多少而定。
定义2 给定一组分类器 h1 ( X), h2 ( X),…, h k ( X),每个分类器的训练集都是从原始的服从随机分布的数据集( Y, X)中随机抽样所得,余量函数(Margin function)定义为
| |
(1) |
式中: I(•)是示性函数。
余量函数用于度量平均正确分类数超过平均错误分类数的程度,余量值越大,分类预测越可靠。
定义3 泛化误差定义为
| |
(2) |
式中:下标 X、 Y表示概率 P覆盖 X、 Y空间。
在随机森林中,当决策树分类器足够多, h k( X)= h( X, θ k)服从强大数定律。
定理1 随着随机森林中决策树数量的增加,所有序列 θ1, θ2,…, θk, PE*几乎处处收敛于
| |
(3) |
定理1表明随机森林不会随着决策树的增加而产生过拟合问题,但可能会产生一定限度内的泛化误差。
变量重要性评估是随机森林算法的一个重要特点。随机森林程序通常提供4种变量重要性度量。本文采用基于袋外数据分类准确率的变量重要性度量。
定义4 基于袋外数据分类准确率的变量重要性度量[ 7]定义为袋外数据自变量值发生轻微扰动后的分类正确率与扰动前分类正确率的平均减少量。
假设有bootstrap样本 b=1,2,…, B, B表示训练样本个数,特征 X j的基于分类准确率的变量重要性度量 D j按照下面的步骤计算:
(1)设置 b=1,在训练样本上创建决策树 T b,并将袋外数据标记为 ![]()
(2)在袋外数据上使用 T b 对 ![]() 数据进行分类,统计正确分类的个数,记为
数据进行分类,统计正确分类的个数,记为 ![]()
(3)对于特征 X j,j=1,2,…, N,对 ![]() 中的特征 Xj的值进行扰动,扰动后的数据集记为
中的特征 Xj的值进行扰动,扰动后的数据集记为 ![]() ,使用 T b 对
,使用 T b 对 ![]() 数据进行分类,统计正确分类的个数,记为
数据进行分类,统计正确分类的个数,记为 ![]()
(4)对于 b=2,3,…, B,重复步骤(1)~(3)。
(5)特征 X j 的变量重要性度量 Dj通过下面的公式进行计算:
| |
(4) |
定义5 随机森林算法的分类准确率定义为
| |
(5) |
式中:TP(true positive)代表正确的肯定;TN(true negative)代表正确的否定;FP(false positive)代表错误的肯定;FN(false negative)代表错误的否定。
本文提出了一种基于随机森林的Wrapper特征选择方法RFFS,利用随机森林算法的变量重要性度量对特征进行排序,然后采用序列后向搜索方法,每次从特征集合中去掉一个最不重要(重要性得分最小)的特征,逐次进行迭代,并计算分类正确率,最终得到变量个数最少、分类正确率最高的特征集合作为特征选择结果。为了保证实验结果的稳定性,本文采用了10折交叉验证方法,在每一次迭代中,将数据集划分成10等份,利用其中的9份作为训练集用于构建随机森林分类器,剩余的1份作为验证集数据进行验证。在10折交叉验证过程中,选择测试集上分类准确率最高的一次迭代产生的变量重要性排序作为删除特征的依据,将10次迭代的平均分类准确率作为该轮迭代的分类精度。具体过程如算法1所示。
算法1 基于随机森林的特征选择算法RFFS
输入:原始数据集S
输出:验证集上的最大分类正确率TGMaxAcc及其对应的特征集合FGSort
步骤:
1.初始化
1.1读入原始数据集S
1.2设置TGMaxAcc=0
2.For(ft in N-2)
2.1 将数据集S随机划分成10等份
2.2 设置局部最大分类准确率TLMaxAcc=0
2.3 设置局部平均分类准确率TLMeanAcc=0
2.4 初始化10折交叉验证中每次迭代的分类准确率
TLAcc[1∶10]=0
2.5 For(i in 1∶10)
2.5.1 在S上运行randomForest创建分类器
2.5.2 在测试集上执行predict进行分类
2.5.3 比较分类结果与观测值,计算TLAcc
2.5.4 计算TLMeanAcc=TLMeanAcc+TLAcc[i]/10
2.5.5 If(TLMaxAcc<=TLAcc[i])
2.5.6 则TLMaxAcc=TLAcc[i]
2.5.7 对特征按变量重要性排序并存为FSort
2.6 If(TGMaxAcc<=TLMeanAcc)
则TGMaxAcc=TLMeanAcc
FGSort=FSort
2.7 从FSort中去掉重要性得分最低的一个特征,得到新的数据集S
3.输出结果
3.1输出全局最高分类准确率TGMaxAcc
3.2输出全局最高分类准确率对应的特征集合FGSort
注:ft代表循环变量,N代表数据集中所有特征个数。
本文所提出的随机森林特征选择方法中基分类器选择CART算法。假设训练数据集的特征维数为 m,训练样本个数为 n, CART算法的时间复杂度为 Ο mnlogn2 。随机森林在构建CART树的过程中,从 m个特征中随机选择 mtry个特征计算信息增益,并且对树的生长不进行剪枝,故训练每一个基分类器的计算时间小于 Ο mnlogn2假设随机森林中基分类器的个数为 k个,则随机森林算法的时间复杂度可以近似为 Οmnlogn2 。在本实验中,采用序列后向选择策略进行特征选择需要循环 m-22次,每一轮循环中采用10折交叉验证,需运行随机森林算法10次,每轮循环需对特征子集进行排序,采用快速排序算法的平均时间复杂度为 Ο mlogm,根据排序后的特征集合生成新的训练数据集需要进行m-2次,每次计算时间为常数,故本算法总的时间复杂度可以近似表示为
| |
(6) |
由式(6)可见,RFFS算法的时间复杂度与特征维数 ![]() 成近似平方关系,与数据集样本个数
成近似平方关系,与数据集样本个数 ![]() 成近似立方关系,对于高维小样本数据,运算时间是可以接受的,算法具有较好的扩展性。
成近似立方关系,对于高维小样本数据,运算时间是可以接受的,算法具有较好的扩展性。
为便于比较,从UCI数据集中选取了wdbc、breast-cancer-wisconsin、pima-indians-diabetes和heart disease4个数据集进行测试。表1列出了这些数据集的特征,数据集维数从几个到数十个不等。
本文算法采用R语言进行实现,随机森林核心算法采用R软件中的randomForest程序包,其中 ![]() 参数取Breiman建议的默认值
参数取Breiman建议的默认值 ![]() 为训练数据集中特征的个数), ntree参数设置为1000。实验的硬件环境为Intel Core(TM)2 Duo CPU [email protected] GHz,3.75 G的内存,操作系统为Microsoft Windows 7,绘图软件采用Matlab7.0。
为训练数据集中特征的个数), ntree参数设置为1000。实验的硬件环境为Intel Core(TM)2 Duo CPU [email protected] GHz,3.75 G的内存,操作系统为Microsoft Windows 7,绘图软件采用Matlab7.0。
本文算法RFFS在搜索实现最大分类准确率的特征子集时采用的是序列后向搜索策略,特征选择过程和结果如图1所示。从图1可以看出,随着不重要特征(在随机森林变量重要性排序中排在最后的特征)的依次删除,分类准确率整体上呈现逐步提高的趋势,这主要是因为不相关特征和冗余特征的消除提高了分类器性能;当分类准确率到达最高值97.98%后又开始呈现下降趋势,则是因为有用的特征被消除,降低了分类器的性能。这说明了本文算法能够有效地识别并消除冗余特征和不相关特征,从而提高分类器的分类性能。
|
|
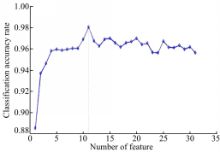 |
图1 分类精度与特征个数之间的关系Fig.1 Relationship between classification accuracy and feature number |
表2列出了RFFS算法和CBFS算法、AMGA算法在不同实验数据集上的性能比较,其中SF列表示选出的最优特征子集中的特征个数,Acc列表示算法在实验数据集上的分类性能。CBFS算法、AMGA算法在相应数据集上的实验数据分别来自文献[ 9]和文献[ 10],“—”表示该算法在相应数据集上没有进行实验。
从表2可以看出,RFFS算法在Breast、Diabetes、和Heart数据集上的分类正确率分别为98.2%、81.1%、92.3%,选择出的特征个数分别为6、5、6。与CBFS算法相比,RFFS算法在特征个数基本相等或者更少的情况下,分类性能明显优于CBFS。RFFS算法在Breast数据集上选择的特征个数与AMGA算法相等,分类性能略低于AMGA算法;在Diabetes数据集上,RFFS算法选择的特征个数与AMGA算法相等,分类性能略高于AMGA算法;在Heart数据集上,RFFS算法比AMGA算法选择了更少的特征数目,却获得了更高的分类精度。从整体上看,本文方法优于文献[ 9]和文献[ 10]中的方法。实验结果表明,RFFS算法不仅能够选择出较优的特征子集,而且能够获得较高的分类性能。
另外,本文算法也可以容易地扩展为使用广义后向搜索策略进行最优子集搜索,为了获得最好的分类效果,本文对删除“最不重要特征”时采用的不同步长进行了实验,结果如表3所示。从表3可以看出,在所有6组实验中(依次删除1个到6个特征),最高的分类性能是在每次删除一个特征时获得。需要说明的是,每次删除一个特征并不是在所有数据集上的最优选择,由于本文所涉及的数据集特征数目还不是特别高,所以每次删除一个特征有助于获取最优子集。当数据集特征数目非常高时,每次删除一个特征就不再适用,因为大量的特征数目将会大大增加时间开销,并且不能快速有效地消除冗余和不相关特征。如何对采用广义后向搜索时的 ![]() 值进行设置,将是下一步研究的方向。
值进行设置,将是下一步研究的方向。
提出了一种基于随机森林的封装式特征选择算法,该算法利用随机森林算法的变量重要性度量对特征进行排序,采用后向序列搜索方法寻找能够训练最优性能分类器的特征子集。实验结果表明本文的特征选择算法可以获得较好的分类性能和特征子集,与以前文献中的方法[ 9, 10]相比具有一定的优势。如何在高维数据集中确定广义后向搜索方法中的 ![]() 值,是下一步的研究内容。
值,是下一步的研究内容。
| [1] | 蒋胜利. 高维数据的特征选择与特征提取研究[D]. 西安: 西安电子科技大学计算机学院, 2011. Jiang Sheng-li. Research on feature selection and feature extraction for high-dimensional data[D]. Xi'an: School of Computer Science and Engineering, Xidian University, 2011. [本文引用:1] |
| [2] | Davies S, Russl S. NP-completeness of searches for smallest possible feature sets[C]∥Proceedings of the AAAI Fall Symposiums on Relevance, Menlo Park, 1994: 37-39. [本文引用:1] |
| [3] | Breiman L. Rand om forests[J]. Machine Learning, 2001, 45(1): 5-32. [本文引用:2] [JCR: 1.467] |
| [4] | Strobl Carolin, Boulesteix Anne-Laure, Kneib Thomas, et al. Conditional variable importance for rand om forests[J]. BMC Bioinformatics, 2008, 9(1): 1-11. [本文引用:1] [JCR: 3.024] |
| [5] | Reif David M, Motsinger Alison A, McKinney Brett A, et al. Feature selection using a rand om forests classifier for the integrated analysis of multiple data types[C]∥IEEE Symposium on Computational Intelligence and Bioinformatics and Computational Biology, 2006: 171-178. [本文引用:1] |
| [6] | Mohammed Khalilia, Sounak Chakraborty, Mihail Popescu. Predicting disease risks from highly imbalanced data using rand om forest[J]. BMC Medical Informatics and Decision Making, 2011, 11(7): 51-58. [本文引用:1][JCR: 1.603] |
| [7] | Verikas A, Gelzinis A, Bacauskiene M. Mining data with rand om forests: a survey and results of new tests[J]. Pattern Recognition, 2011, 44(2): 330-349. [本文引用:2] [JCR: 2.632] |
| [8] | Inza I, Larranaga P, Blanco R. Filter versus wrapper gene selection approaches in DNA microarray domains[J]. Artificial Intelligence in Medicine, 2004, 31(2): 91-103. [本文引用:1] [JCR: 1.355] |
| [9] | 蒋盛益, 郑琪, 张倩生. 基于聚类的特征选择方法[J]. 电子学报, 2008, 36(12): 157-160. Jiang Sheng-yi, Zheng Qi, Zhang Qian-sheng. Clustering-based feature selection[J]. Acta Electronica Sinica,2008, 36(12): 157-160. [本文引用:3] [CJCR: 0.686] |
| [10] | 刘元宁, 王刚, 朱晓冬, 等. 基于自适应多种群遗传算法的特征选择[J]. 吉林大学学报: 工学版, 2011, 41(6): 1690-1693. Liu Yuan-ning, Wang Gang, Zhu Xiao-dong, et al. Feature selection based on adaptive multi-population genetic algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(6): 1690-1693.[本文引用:3] [CJCR: 0.701] |
