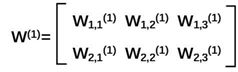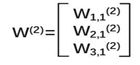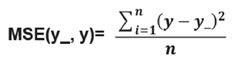人工智能实践:TensorFlow笔记学习(三)——TensorFlow框架
搭建神经网络
大纲
3.1 张量、计算图、会话
3.2 前向传播
3.3 反向传播
目标
搭建神经网络,总结搭建八股
3.1 张量、计算图、会话
一、基本概念
基于Tensorflow的NN:用张量表示数据,用计算图搭建神经网络,用会话执行计算图,优化线上的权重(参数),得到模型。
张量:张量就是多维数组(列表),用“阶”表示张量的维度。
0阶张量称作标量,表示一个单独的数;
举例 S=123
1阶张量称作向量,表示一个一维数组;
举例 V=[1,2,3]
2阶张量称作矩阵,表示一个二维数组,它可以有i行j列个元素,每个元素可以用行号和列号共同索引到;
举例 m=[[1, 2, 3], [4, 5, 6], [7, 8, 9]]
判断张量是几阶的,就通过张量右边的方括号数,0个是0阶,n个是n阶,张量可以表示0阶到n阶数组(列表);
举例 t=[ [ [… ] ] ]为3阶。
数据类型:Tensorflow的数据类型有tf.float32、tf.int32等。
举例
我们实现Tensorflow的加法:
#引入模块
import tensorflow as tf
#定义一个张量等于[1.0,2.0]
a=tf.constant([1.0,2.0])
#定义一个张量等于[3.0,4.0]
b=tf.constant([3.0,4.0])
#实现a加b的加法
result=a+b
#打印出结果 可以打印出这样一句话:
#Tensor(“add:0”, shape=(2, ), dtype=float32)
#意思为result是一个名称为add:0的张量,shape=(2,)表示一维数组长度为2,dtype=float32表示数据类型为浮点型。
print result计算图(Graph):搭建神经网络的计算过程,是承载一个或多个计算节点的一张图,只搭建网络,不运算。
举例
在第一讲中我们曾提到过,神经网络的基本模型是神经元,神经元的基本模型其实就是数学中的乘、加运算。
我们搭建如下的计算图:
x1、x2表示输入,w1、w2分别是x1到y和x2到y的权重,y=x1*w1+x2*w2。
我们实现上述计算图:
#引入模块
import tensorflow as tf
#定义一个2阶张量等于[[1.0,2.0]]
x = tf.constant([[1.0, 2.0]])
#定义一个2阶张量等于[[3.0],[4.0]]
w = tf.constant([[3.0], [4.0]])
#实现xw矩阵乘法
y=tf.matmul(x,w)
#打印出结果 可以打印出这样一句话:Tensor(“matmul:0”, shape(1,1), dtype=float32),
print y
#执行会话并打印出执行后的结果
#可以打印出这样的结果:[[11.]]
with tf.Session() as sess:
print sess.run(y)
从这里我们可以看出,print的结果显示y是一个张量,只搭建承载计算过程的计算图,并没有运算,如果我们想得到运算结果就要用到“会话Session()”了。
会话(Session):执行计算图中的节点运算。我们用with结构实现,语法如下:
with tf.Session() as sess:
print sess.run(y)上面代码会话后打印出了y的结果1.0*3.0+ 2.0*4.0 = 11.0。
注意:
①:我们以后会常用到vim编辑器,为了使用方便,我们可以更改vim的配置文件,使vim的使用更加便捷。
我们在vim~/.vimrc 写入:
set ts=4 表示使Tab键等效为4个空格
set nu 表示使vim显示行号 nu是number缩写
②:在vim编辑器中运行Session()会话时,有时会出现“提示warning”,是因为有的电脑可以支持加速指令,但是运行代码时并没有启动这些指令。可以把这些“提示warning”暂时屏蔽掉。屏蔽方法为进入主目录下的bashrc文件,在bashrc 文件中加入这样一句 export TF_CPP_MIN_LOG_LEVEL=2,从而把“提示 warning”等级降低。source 命令用于重新执行修改的初始化文件,使之立即生效,而不必注销并重新登录。
vim ~/.bashrc
source ~/.bashrc
3.2 前向传播
一、神经网络的参数
神经网络的参数:是指神经元线上的权重w,用变量表示,一般会先随机生成这些参数。
生成参数的方法是让w等于tf.Variable,把生成的方式写在括号里。 神经网络中常用的生成随机数/数组的函数有:
tf.random_normal() 生成正态分布随机数
tf.truncated_normal() 生成去掉过大偏离点的正态分布随机数
tf.random_uniform() 生成均匀分布随机数
tf.zeros 表示生成全0数组
tf.ones 表示生成全1数组
tf.fill 表示生成全定值数组
tf.constant 表示生成直接给定值的数组
举例
① w=tf.Variable(tf.random_normal([2,3],stddev=2, mean=0, seed=1))
表示生成正态分布随机数,形状两行三列,标准差是2,均值是0,随机种子是1。
② w=tf.Variable(tf.Truncated_normal([2,3],stddev=2, mean=0, seed=1)),
表示去掉偏离过大的正态分布,也就是如果随机出来的数据偏离平均值超过两个标准差,这个数据将重新生成。
③ w=random_uniform(shape=7,minval=0,maxval=1,dtype=tf.int32,seed=1),
表示从一个均匀分布[minval maxval)中随机采样,注意定义域是左闭右开,即包含minval,不包含maxval。
④ 除了生成随机数,还可以生成常量。
tf.zeros([3,2],int32)表示生成[[0,0],[0,0],[0,0]];
tf.ones([3,2],int32)表示生成[[1,1],[1,1],[1,1];
tf.fill([3,2],6)表示生成[[6,6],[6,6],[6,6]];
tf.constant([3,2,1])表示生成[3,2,1]。
注意:
①随机种子如果去掉每次生成的随机数将不一致。
②如果没有特殊要求标准差、均值、随机种子是可以不写的。
二、神经网络的搭建
当我们知道张量、计算图、会话和参数后,我们可以讨论神经网络的实现过程了。
神经网络的实现过程:
1、准备数据集,提取特征,作为输入喂给神经网络(Neural Network,NN)
2、搭建NN结构,从输入到输出(先搭建计算图,再用会话执行)
( NN前向传播算法 -----> 计算输出)
3、大量特征数据喂给NN,迭代优化NN参数
( NN反向传播算法 -----> 优化参数训练模型)
4、使用训练好的模型预测和分类
由此可见,基于神经网络的机器学习主要分为两个过程,即训练过程和使用过程。
训练过程是第一步、第二步、第三步的循环迭代,使用过程是第四步,一旦参数优化完成就可以固定这些参数,实现特定应用了。很多实际应用中,我们会先使用现有的成熟网络结构,喂入新的数据,训练相应模型,判断是否能对喂入的从未见过的新数据作出正确响应,再适当更改网络结构,反复迭代,让机器自动训练参数找出最优结构和参数,以固定专用模型。
三、前向传播
前向传播就是搭建模型的计算过程,让模型具有推理能力,可以针对一组输入给出相应的输出。
举例
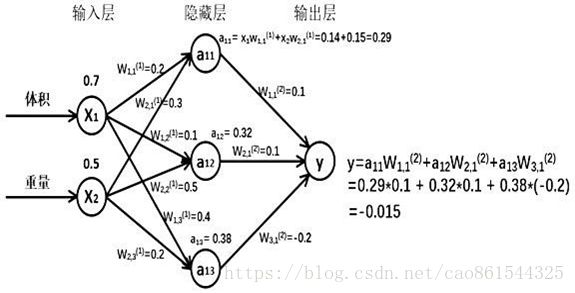
假如生产一批零件,体积为x1,重量为x2,体积和重量就是我们选择的特征,把它们喂入神经网络,当体积和重量这组数据走过神经网络后会得到一个输出。
假如输入的特征值是:体积0.7 重量0.5
由搭建的神经网络可得,隐藏层节点a11=x1*w11+x2*w21=0.14+0.15=0.29,同理算得节点a12=0.32,a13=0.38,最终计算得到输出层Y=-0.015,这便实现了前向传播过程。
推导:
第一层 X是输入为1X2矩阵 用x表示输入,是一个1行2列矩阵,表示一次输入一组特征,这组特征包含了 体积和重量两个元素。
W 前节点编号,后节点编号(层数) 为待优化的参数
对于第一层的w 前面有两个节点,后面有三个节点 w应该是个两行三列矩阵,
我们这样表示:
神经网络共有几层(或当前是第几层网络)都是指的计算层,输入不是计算层,所以a为第一层网络,a是一个一行三列矩阵。
我们这样表示:a(1)=[a11, a12, a13]=XW(1)
第二层参数要满足前面三个节点,后面一个节点,所以W(2) 是三行一列矩阵。 我们这样表示:
我们把每层输入乘以线上的权重w,这样用矩阵乘法可以计算出输出y了。
a= tf.matmul(X,W1)
y= tf.matmul(a, W2)
由于需要计算结果,就要用with结构实现,所有变量初始化过程、计算过程都要放到 sess.run 函数中。
对于变量初始化,我们在sess.run中写入tf.global_variables_initializer实现对所有变量初始化,也就是赋初值。对于计算图中的运算,我们直接把运算节点填入sess.run 即可,比如要计算输出y,直接写 sess.run(y) 即可。
在实际应用中,我们可以一次喂入一组或多组输入,让神经网络计算输出y,可以先用tf.placeholder给输入占位。
如果一次喂一组数据shape的第一维位置写1,第二维位置看有几个输入特征;
如果一次想喂多组数据,shape的第一维位置可以写None表示先空着,第二维位置写有几个输入特征。
这样在feed_dict中可以喂入若干组体积重量了。
举例 这是一个实现神经网络前向传播过程,网络可以自动推理出输出y的值。
①用placeholder实现输入定义(sess.run中喂入一组数据)的情况 第一组喂体积0.7、重量0.5
#coding:utf-8
#两层简单神经网络(全连接)
import tensorflow as tf
#定义输入和参数
#用placeholder实现输入定义 (sess.run中喂一组数据)
x = tf.placeholder(tf.float32, shape=(1, 2))
w1= tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2= tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
#定义前向传播过程
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)
#用会话计算结果
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
print"y in tf3_4.py is:\n",sess.run(y, feed_dict={x: [[0.7,0.5]]})②用placeholder实现输入定义(sess.run中喂入多组数据)的情况第一组喂体积0.7、重量0.5,第二组喂体积0.2、重量0.3,第三组喂体积0.3 、重量0.4,第四组喂体积0.4、重量0.5.
#coding:utf-8
#两层简单神经网络(全连接)
import tensorflow as tf
#定义输入和参数
#用placeholder定义输入(sess.run喂多组数据)
x = tf.placeholder(tf.float32, shape=(None, 2))
w1= tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2= tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
#定义前向传播过程
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)
#调用会话计算结果
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
print "the result of tf3_5.py is:\n",sess.run(y, feed_dict={x: [[0.7,0.5],[0.2,0.3],[0.3,0.4],[0.4,0.5]]})
print "w1:\n", sess.run(w1)
print "w2:\n", sess.run(w2)3.3 反向传播
一、反向传播
反向传播:训练模型参数,在所有参数上用梯度下降,使NN模型在训练数据上的损失函数最小。
损失函数(loss):计算得到的预测值y与已知答案y_的差距。
损失函数的计算有很多方法,均方误差MSE是比较常用的方法之一。
均方误差MSE:求前向传播计算结果与已知答案之差的平方再求平均。
用tensorflow函数表示为:
loss_mse =tf.reduce_mean(tf.square(y_ - y))
反向传播训练方法:
以减小loss值为优化目标,有梯度下降、momentum优化器、adam优化器等优化方法。
这三种优化方法用tensorflow的函数可以表示为:
train_step=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
train_step=tf.train.MomentumOptimizer(learning_rate, momentum).minimize(loss)
train_step=tf.train.AdamOptimizer(learning_rate).minimize(loss)
三种优化方法区别如下:
①tf.train.GradientDescentOptimizer()
使用随机梯度下降算法,使参数沿着梯度的反方向,即总损失减小的方向移动,实现更新参数。
②tf.train.MomentumOptimizer()
在更新参数时,利用了超参数,实现更新参数。
③tf.train.AdamOptimizer()
是利用自适应学习率的优化算法,Adam 算法和随机梯度下降算法不同。随机梯度下降算法保持单一的学习率更新所有的参数,学习率在训练过程中并不会改变。而 Adam 算法通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。 学习率:决定每次参数更新的幅度。优化器中都需要一个叫做学习率的参数,使用时,如果学习率选择过大会出现震荡不收敛的情况,如果学习率选择过小,会出现收敛速度慢的情况。我们可以选个比较小的值填入,比如0.01、0.001。
二、搭建神经网络的八股
我们最后梳理出神经网络搭建的八股,神经网络的搭建课分四步完成:准备工作、前向传播、反向传播和循环迭代。
0.导入模块,生成模拟数据集
import
常量定义
生成数据集
1.前向传播:定义输入、参数和输出
x= y_=
w1= w2=
a= y=
2. 反向传播:定义损失函数、反向传播方法
loss=
train_step=
3. 生成会话,训练STEPS轮
with tf.session() as sess
Init_op=tf. global_variables_initializer()
sess_run(init_op)
STEPS=3000 for i in range(STEPS):
start= end=
sess.run(train_step, feed_dict:)
举例
随机产生32组生产出的零件的体积和重量,训练3000轮,每500轮输出一次损失函数。
下面我们通过源代码进一步理解神经网络的实现过程:
#coding:utf-8
#0导入模块,生成模拟数据集。
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8
SEED = 23455
#基于seed产生随机数
rdm = np.random.RandomState(SEED)
#随机数返回32行2列的矩阵 表示32组 体积和重量 作为输入数据集
X = rdm.rand(32,2)
#从X这个32行2列的矩阵中 取出一行 判断如果和小于1 给Y赋值1 如果和不小于1 给Y赋值0
#作为输入数据集的标签(正确答案)
Y_ = [[int(x0 + x1 < 1)] for (x0, x1) in X]
print "X:\n",X
print "Y_:\n",Y_
#1定义神经网络的输入、参数和输出,定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_= tf.placeholder(tf.float32, shape=(None, 1))
w1= tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2= tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)
#2定义损失函数及反向传播方法。
loss_mse = tf.reduce_mean(tf.square(y-y_))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mse)
#train_step = tf.train.MomentumOptimizer(0.001,0.9).minimize(loss_mse)
#train_step = tf.train.AdamOptimizer(0.001).minimize(loss_mse)
#3生成会话,训练STEPS轮
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
# 输出目前(未经训练)的参数取值。
print "w1:\n", sess.run(w1)
print "w2:\n", sess.run(w2)
print "\n"
# 训练模型。
STEPS = 3000
for i in range(STEPS):
start = (i*BATCH_SIZE) % 32
end = start + BATCH_SIZE
sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
if i % 500 == 0:
total_loss = sess.run(loss_mse, feed_dict={x: X, y_: Y_})
print("After %d training step(s), loss_mse on all data is %g" % (i, total_loss))
# 输出训练后的参数取值。
print "\n"
print "w1:\n", sess.run(w1)
print "w2:\n", sess.run(w2)由神经网络的实现结果,我们可以看出,总共训练3000轮,每轮从X的数据集 和Y的标签中抽取相对应的从start开始到end结束个特征值和标签,喂入神经网络,用sess.run求出loss,每500轮打印一次loss值。经过3000轮后,我们打印出最终训练好的参数w1、w2。
这样四步就可以实现神经网络的搭建了。
致谢
感谢曹老师的辛勤付出,来源曹健,人工智能实践:TensorFlow笔记,北京大学
网址:https://www.icourse163.org/course/PKU-1002536002