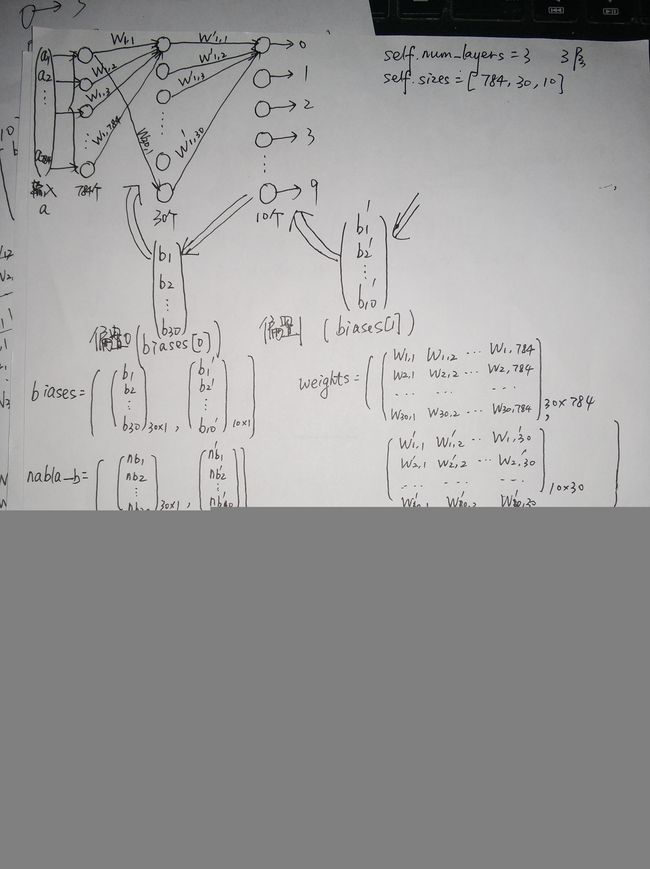
神经网络与深度学习 1.6 使用Python实现基于梯度下降算法的神经网络和MNIST数据集的手写数字分类程序

"""
一个实现了随机梯度下降学习算法的前馈神经网络模块。
梯度的计算使用到了反向传播。
由于我专注于使代码简介、易读且易于修改，所以它不是最优化的，省略了许多令人满意的特性。
"""

#### Libraries
#标准库
import random

#第三方库
import numpy as np

class Network(object):

    def __init__(self, sizes):
        """
        在这段代码中，列表 sizes 包含各层神经元的数量。例如，如果我们想创建⼀个在第⼀层有
        2 个神经元，第⼆层有 3 个神经元，最后层有 1 个神经元的 Network 对象，我们应这样写代码：
        net = Network([2, 3, 1])
        Network 对象中的偏置和权重都是被随机初始化的，使⽤ Numpy 的 np.random.randn 函数来⽣
        成均值为 0，标准差为 1 的⾼斯分布。这样的随机初始化给了我们的随机梯度下降算法⼀个起点。
        在后⾯的章节中我们将会发现更好的初始化权重和偏置的⽅法，但是⽬前随机地将其初始化。
        注意 Network 初始化代码假设第⼀层神经元是⼀个输⼊层，并对这些神经元不设置任何偏置，
        因为偏置仅在后⾯的层中⽤于计算输出。
        """
        self.num_layers = len(sizes)
        #num_layers为层数
        self.sizes = sizes
        #列表 sizes 包含各层神经元的数量
        self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
        """
        print(np.random.randn(2,4))  # 生成2行4列服从标准正态分布的随机数
        sizes[0]是第一层的神经元个数，由于它是输入层，不设置偏置，所以循环从1开始，for y in sizes[1:]]
        sizes[1]是第二层的神经元个数，例如，y=sizes[1]=30，则表示第二层有30个神经元，则
        用np.random.randn(y, 1)生成一个30行一列服从标准正态分布的随机数，即一个30行1列的偏置向量
        sizes[2]是第三层的神经元个数，例如，y=sizes[2]=10，则表示第三层有10个神经元，则
        用np.random.randn(y, 1)生成一个10行一列服从标准正态分布的随机数，即一个10行1列的偏置向量
        ...
        这些偏置向量构成一个偏置向量组存放在biases中.
        biases[0]是30行一列的向量
        biases[1]是10行一列的向量
        """
        self.weights = [np.random.randn(y, x)
                        for x, y in zip(sizes[:-1], sizes[1:])]
        """
            sizes = [784,30,10]
            for x, y in zip(sizes[:-1], sizes[1:]):
                print(y,x)
            输出结果为：
            30 784
            10 30
            sizes[:-1]意为从第一个（下标为0）到最后一个(下标为-1)
            sizes[1:] 意为从第二个（下标为1）到最后一个(下标为-1)
            所以对于sizes = [784,30,10]的神经网络
            依次生成30行784列的向量，10行30列的向量存放到weights中
            weights[0]是30行784列的向量，weights[1]是10行30列的向量
        """
    def feedforward(self, a):
        """如果a是输入，则返回网络的输出"""
        for b, w in zip(self.biases, self.weights):
            a = sigmoid(np.dot(w, a)+b)
        """
            对于每一层（除掉第一层输入层，这也是为什么三层网络中weights和biases的len均为2），
            用该层的权重向量与输入向量作点积并加上偏置，即z=w*a+b
            然后调用sigmoid函数得到s函数的结果并返回，即求σ(z)=1/(1+e^-z)
        """
        return a
        """
            weights[0] 30*784矩阵
            a 原始输入 784*1矩阵
            biases[0] 30*1矩阵
            故weights[0]*a为30*1矩阵，weights[0]*a+biases[0]为30*1矩阵
            
            然后将其赋值给a，此时a变为30*1矩阵
            
            weights[1] 10*30矩阵
            a 上步结果，30*1矩阵
            biases[1] 10*1矩阵
            故weights[1]*a为10*1矩阵，weights[1]*a+biases[1]为10*1矩阵
            
            然后将其赋值给a，此时a变为10*1矩阵
            
            return a
            所以最后结果为10行1列矩阵（向量），对应于0，1，2，3，4，5，6，7，8，9的可能性
        """

    def SGD(self, training_data, epochs, mini_batch_size, eta,
            test_data=None):
        """
        :param training_data: training_data 是一个 (x, y) 元组的列表，表⽰训练输⼊和其对应的期望输出。
        :param epochs: 变量 epochs为迭代期数量
        :param mini_batch_size: 变量mini_batch_size为采样时的⼩批量数据的⼤⼩
        :param eta: 学习速率
        :param test_data: 如果给出了可选参数 test_data ，那么程序会在每个训练器后评估⽹络，并打印出部分进展。
        这对于追踪进度很有⽤，但相当拖慢执⾏速度。
        :return:
        """

        training_data = list(training_data)
        #将训练数据集强转为list
        n = len(training_data)
        #n为训练数据总数，大小等于训练数据集的大小
        if test_data:
        #如果有测试数据集
            test_data = list(test_data)
            #将测试数据集强转为list
            n_test = len(test_data)
            # n_test为测试数据总数，大小等于测试数据集的大小
        for j in range(epochs):
        #对于每一个迭代期
            random.shuffle(training_data)
            #shuffle() 方法将序列的所有元素随机排序。
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in range(0, n, mini_batch_size)]
            """
                对于下标为0到n-1中的每一个下标，最小数据集为从训练数据集中下标为k到下标为k+⼩批量数据的⼤⼩-1之间的所有元素
                这些最小训练集组成的集合为mini_batches
                mini_batches[0]=training_data[0:0+mini_batch_size]
                mini_batches[1]=training_data[mini_batch_size:mini_batch_size+mini_batch_size]
                ...
            """
            for mini_batch in mini_batches:
            #对于最小训练集组成的集合mini_batches中的每一个最小训练集mini_batch
                self.update_mini_batch(mini_batch, eta)
                #调用梯度下降算法
            if test_data:
            #如果有测试数据集
                print("Epoch {} : {} / {}".format(j,self.evaluate(test_data),n_test));
                #j为迭代期序号
                #evaluate(test_data)为测试通过的数据个数
                #n_test为测试数据集的大小
            else:
                print("Epoch {} complete".format(j))

    def update_mini_batch(self, mini_batch, eta):
        """
        基于反向传播的简单梯度下降算法更新网络的权重和偏置
        :param mini_batch: 最小训练集
        :param eta: 学习速率
        :return:
        """
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        for b in self.biases:
            print("b.shape=", b.shape)
        """
        运行
        for b in self.biases:
            print("b.shape=",b.shape)
        输出(30，1) (10，1)
        np.zeros((a b))为生成a行b列的数组且每一个元素为0
        所以依次生成一个30行1列的数组和一个10行1列的数组，存放到nabla_b中
        nabla_b[0]为30行1列的数组，每一个元素为0
        nabla_b[1]为10行1列的数组，每一个元素为0
        """

        nabla_w = [np.zeros(w.shape) for w in self.weights]

        """
        同理
         nabla_w[0]为30行784列的数组，每一个元素为0
        nabla_w[1]为10行30列的数组，每一个元素为0
        """
        for x, y in mini_batch:
        #对于最小训练集中的每一个训练数据x及其正确分类y
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            """
            这行调用了一个称为反向传播的算法，一种快速计算代价函数的梯度的方法。
            delta_nabla_b[0]与biases[0]和nabla_b[0]一样为30*1数组（向量）
            delta_nabla_b[1]与biases[1]和nabla_b[1]一样为10*1数组（向量）
            delta_nabla_w[0]与weights[0]和nabla_w[0]一样为30*784数组（向量）
            delta_nabla_w[1]与weights[1]和nabla_w[1]一样为10*30数组（向量）
            """
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            #nabla_b中的每一个即为∂C/∂b
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        # nabla_b中的每一个即为∂C/∂w
        self.weights = [w-(eta/len(mini_batch))*nw
                        for w, nw in zip(self.weights, nabla_w)]
        #更新权重向量组
        self.biases = [b-(eta/len(mini_batch))*nb
                       for b, nb in zip(self.biases, nabla_b)]
        #更新偏置向量组


    def backprop(self, x, y):
    # 反向传播的算法，一种快速计算代价函数的梯度的方法。
        """Return a tuple ``(nabla_b, nabla_w)`` representing the
        gradient for the cost function C_x.  ``nabla_b`` and
        ``nabla_w`` are layer-by-layer lists of numpy arrays, similar
        to ``self.biases`` and ``self.weights``."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass
        delta = self.cost_derivative(activations[-1], y) * \
            sigmoid_prime(zs[-1])
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        for l in range(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

    def evaluate(self, test_data):
        """Return the number of test inputs for which the neural
        network outputs the correct result. Note that the neural
        network's output is assumed to be the index of whichever
        neuron in the final layer has the highest activation."""
        test_results = [(np.argmax(self.feedforward(x)), y)
                        for (x, y) in test_data]
        return sum(int(x == y) for (x, y) in test_results)

    def cost_derivative(self, output_activations, y):
        """Return the vector of partial derivatives \partial C_x /
        \partial a for the output activations."""
        return (output_activations-y)

#### Miscellaneous functions
def sigmoid(z):
    """The sigmoid function."""
    return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
    #计算 σ函数的导数
    """Derivative of the sigmoid function."""
    return sigmoid(z)*(1-sigmoid(z))

使用如下代码加载训练数据:

# %load mnist_loader.py
"""
mnist_loader
~~~~~~~~~~~~
A library to load the MNIST image data.  For details of the data
structures that are returned, see the doc strings for ``load_data``
and ``load_data_wrapper``.  In practice, ``load_data_wrapper`` is the
function usually called by our neural network code.
"""

#### Libraries
# Standard library
import pickle
import gzip

# Third-party libraries
import numpy as np

def load_data():
    """Return the MNIST data as a tuple containing the training data,
    the validation data, and the test data.
    The ``training_data`` is returned as a tuple with two entries.
    The first entry contains the actual training images.  This is a
    numpy ndarray with 50,000 entries.  Each entry is, in turn, a
    numpy ndarray with 784 values, representing the 28 * 28 = 784
    pixels in a single MNIST image.
    The second entry in the ``training_data`` tuple is a numpy ndarray
    containing 50,000 entries.  Those entries are just the digit
    values (0...9) for the corresponding images contained in the first
    entry of the tuple.
    The ``validation_data`` and ``test_data`` are similar, except
    each contains only 10,000 images.
    This is a nice data format, but for use in neural networks it's
    helpful to modify the format of the ``training_data`` a little.
    That's done in the wrapper function ``load_data_wrapper()``, see
    below.
    """
    f = gzip.open('mnist.pkl.gz', 'rb')
    training_data, validation_data, test_data = pickle.load(f, encoding="latin1")
    f.close()
    return (training_data, validation_data, test_data)

def load_data_wrapper():
    """Return a tuple containing ``(training_data, validation_data,
    test_data)``. Based on ``load_data``, but the format is more
    convenient for use in our implementation of neural networks.
    In particular, ``training_data`` is a list containing 50,000
    2-tuples ``(x, y)``.  ``x`` is a 784-dimensional numpy.ndarray
    containing the input image.  ``y`` is a 10-dimensional
    numpy.ndarray representing the unit vector corresponding to the
    correct digit for ``x``.
    ``validation_data`` and ``test_data`` are lists containing 10,000
    2-tuples ``(x, y)``.  In each case, ``x`` is a 784-dimensional
    numpy.ndarry containing the input image, and ``y`` is the
    corresponding classification, i.e., the digit values (integers)
    corresponding to ``x``.
    Obviously, this means we're using slightly different formats for
    the training data and the validation / test data.  These formats
    turn out to be the most convenient for use in our neural network
    code."""
    tr_d, va_d, te_d = load_data()
    training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
    training_results = [vectorized_result(y) for y in tr_d[1]]
    training_data = zip(training_inputs, training_results)
    validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
    validation_data = zip(validation_inputs, va_d[1])
    test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
    test_data = zip(test_inputs, te_d[1])
    return (training_data, validation_data, test_data)

def vectorized_result(j):
    """Return a 10-dimensional unit vector with a 1.0 in the jth
    position and zeroes elsewhere.  This is used to convert a digit
    (0...9) into a corresponding desired output from the neural
    network."""
    e = np.zeros((10, 1))
    e[j] = 1.0
    return e

调度程序如下：

import mnist_loader
training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
training_data = list(training_data)

import network
net = network.Network([784, 30, 10])
net.SGD(training_data, 30, 10, 3.0, test_data=test_data)