AI（008） - 循环神经网络（Recurrent Neural Network）

循环神经网络（Recurrent Neural Network）

AI-第五期-DarkRabbit

这篇文章是对循环神经网络的一个概念性总结，对应：

• 第十一周：（01）循环神经网络
• 第十一周：（04）LSTM
• 维基百科（en）：
  
  • “Recurrent neural network” 词条
  • “Long short-term memory” 词条
  • “Backpropagation through time” 词条

公式在CSDN的app中会显示乱码，请在其它方式阅读

---

目录

---

1 什么是循环神经网络

循环神经网络是一种人工神经网络（Artificial Neural Network），它的神经元间的连接沿序列（sequence）构成有向图，这使得它能表现出动态时间行为，所以有些地方也称为时间递归神经网络。

2 常用结构（Architectures）

2.1 基本结构（Basic）

基本循环神经网络结构（图片来自 Wikipedia）：

从图中可以看出（ t t 为时间，除时间外所指均为向量或矩阵，下同）：

• 输入层（input）：在 t t 时刻的输入 xt x t 。
• 隐藏层（hidden）：在 t t 时刻的值 ht h t ，它取决于权重为 U U 的 xt x t 与 权重为 V V 的 ht−1 h t − 1 。
• 输出层（output）：在 t t 时刻的输出 ot o t ，它取决于权重为 W W 的 ht h t 。

用公式表示即是：

otht=σo(Wht)=σh(Uxt+Vht−1)(1)(2) o t = σ o ( W h t ) ( 1 ) h t = σ h ( U x t + V h t − 1 ) ( 2 )

其中 σ(⋅) σ ( ⋅ ) 为对应的激活函数。

从公式(2)表现为递归形式来看，输出 ot o t 是受到之前所有输入的影响（ xt,xt−1,⋯ x t , x t − 1 , ⋯ ）。展开式为：

ot=σo(Wht)=σo(W⋅σh(Uxt+Vht−1))=σo(W⋅σh(Uxt+V⋅σh(Uxt−1+Vht−2)))=σo(W⋅σh(Uxt+V⋅σh(Uxt−1+V⋅σh(Uxt−2+V⋅σh(⋯)))))(3) o t = σ o ( W h t ) = σ o ( W ⋅ σ h ( U x t + V h t − 1 ) ) = σ o ( W ⋅ σ h ( U x t + V ⋅ σ h ( U x t − 1 + V h t − 2 ) ) ) = σ o ( W ⋅ σ h ( U x t + V ⋅ σ h ( U x t − 1 + V ⋅ σ h ( U x t − 2 + V ⋅ σ h ( ⋯ ) ) ) ) ) ( 3 )

2.2 简单结构（Simple Recurrent (Neural) Networks，SR(N)N）

简单循环网络（SRN）通常是指 Elman networks 与 Jordan networks 。

Elman 网络的结构（图片来自 Wikipedia）：

Elman 网络是一个三层网络（图中 x,y,z x , y , z ），附带一个“上下文单元”（context units，图中 u u ）。隐层与这些单元相连接，权重为1。

Jordan 网络和 Elman 网络非常相似。只是这些“上下文单元”不是和隐层相连，而是与输出层相连。这些“上下文单元”被称为状态层（state layer）。

它们的公式表示都为：

ytht=σy(Wyht+by)=σh(Whxt+Uhht−1+bh)(4)(5) y t = σ y ( W y h t + b y ) ( 4 ) h t = σ h ( W h x t + U h h t − 1 + b h ) ( 5 )

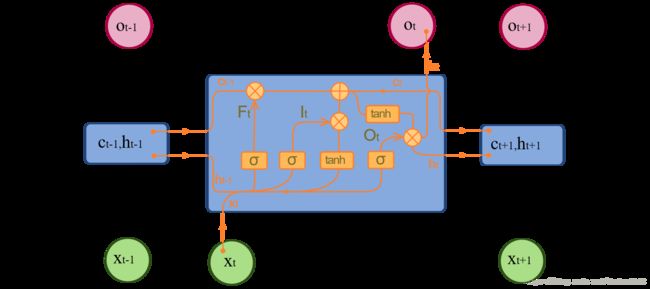
2.3 长短期记忆网络（Long Short-Term Memory，LSTM）

LSTM 避免了梯度消失的问题。

LSTM 结构如下（图片来自 Wikipedia）：

一个 LSTM 包含一个记忆细胞（memory cell，图中 ct c t ），一个遗忘门（forget gate，图中 σ,Ft σ , F t ）一个输入门（input gate，图中 σ,It σ , I t ）和一个输出门（output gate，图中 σ,Ot σ , O t ）。

从图中就可以看出，在 LSTM 有：

• 遗忘门：决定了上一时刻 ct−1 c t − 1 保留多少内容。
• 输入门：决定了这一时刻 xt x t 保留多少内容。
• 输出门：决定了这一时刻 ct c t 有多少内容输出到 ht h t 。
• 输入：在 t t 时刻的输入 xt x t ，在 t−1 t − 1 时刻的输出 ht−1 h t − 1 和 ct−1 c t − 1 。
• 输出：在 t t 时刻的输出 ht h t 和 ct c t 。

用公式表示即是：

FtItOtctht=sigmoid(WFxt+UFht−1+bF)=sigmoid(WIxt+UIht−1+bI)=sigmoid(WOxt+UOht−1+bO)=Ft∘ct−1+It∘tanh(Wcxt+Ucht−1+bc)=Ot∘tanh(ct)(6)(7)(8)(9)(10) F t = s i g m o i d ( W F x t + U F h t − 1 + b F ) ( 6 ) I t = s i g m o i d ( W I x t + U I h t − 1 + b I ) ( 7 ) O t = s i g m o i d ( W O x t + U O h t − 1 + b O ) ( 8 ) c t = F t ∘ c t − 1 + I t ∘ tanh ⁡ ( W c x t + U c h t − 1 + b c ) ( 9 ) h t = O t ∘ tanh ⁡ ( c t ) ( 10 )

其中 ∘ ∘ 是哈达马乘积（Hadamard product）矩阵运算，也记作 ∗ ∗ ，部分文章也写作 ⊙ ⊙ 。

3 基于时间的反向传播算法（Backpropagation Trough Time，BPTT）

BPTT 是一种基于梯度的技术，可以用来计算 Elman 网络。

具体的计算可以参考这篇文章

Recurrent Neural Networks Tutorial, Part 3 – Backpropagation Through Time and Vanishing Gradients