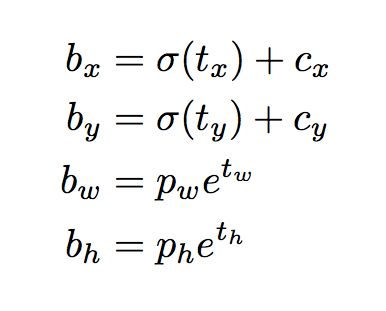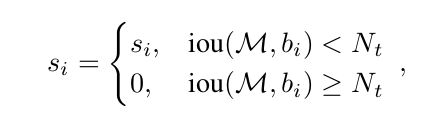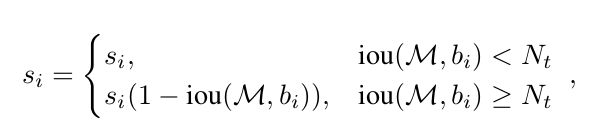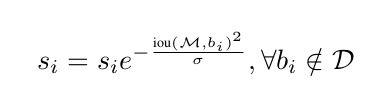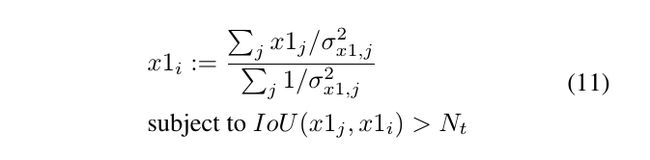深度学习之目标检测综述

  这里是自己这几天读过的几篇论文的笔记，美其名曰为“综述”。
  当年AlexNet 掀起 CNN 网络热潮，深度学习也逐渐被应用到目标检测(object detection)中(rbg 大神的开山之作 R-CNN)。本文一方面主要包括 one-stage detector, two stage detector 以及其它的衍生结构。另一方面也介绍一下近几年在 object detection pipeline 中的 NMS (non-max-suppression) 的一些变体，文章中涉及的论文或者是参考的博客都已在文末给出，希望大家不吝指教~

Serveral Detectors

One Stage Detector and Two Stage Detector

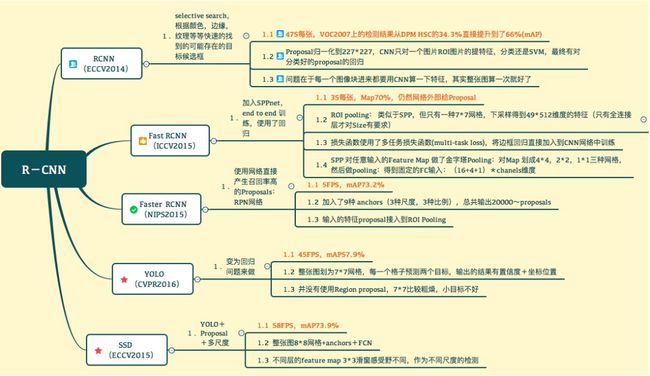
  顾名思义，与two-stage相对的one-stage表示的是单阶段，即无需经过候选框提取(ROI region of interest)的步骤，也因而具有更快的速度。这类 detector 主要包括比较早的 YOLOv1, YOLOv2, SSD(single shot detector), YOLOv3 等等。而 Two stage detector主要是R-CNN系列，包括后来的以 FPN 为 backbone 的 mask rcnn等，往往有更高的准确率。下面借用七月在线的一张图串联几个网络

MultiBox

  Scalable High Quality Object Detection¹最初是由 Inception Net²的作者Szegedy发表在2014年的CVPR上，后来经过修改的第二版在2015年底发出，这边主要讨论修改后的版本。

Motivation

• MultiBox指出了基于特征(salience-based)的region proposal虽然可以涵盖绝大多数的objects,但是比较低效(因为所有proposal的地位相同，没有ranking,数量过多，效率也就低了), 因此希望能以更少但是质量更高的proposal来覆盖objects, 从而提升模型的速度。
  
• 人工设计特征一个是工作量大，一个是task-specific(泛化能力不强)，作者希望能通过提出可学习的region proposal方式提升网络适应不同场景的能力
  

Priors

  Priors(先验)是MultiBox中一个比较重要的概念，类似与r-cnn中的anchor,但是也有不同: 本文中的priors是不同的feature map有各自的anchors(每个feature map的每个grid被赋予11个prior(除了1*1的map)，有利于检测不同尺度的物体)，论文中给出的priors数量:
$$1+11\times (8\times 8+6\times 6+4\times 4+3\times 3+2\times 2))=1420$$而faster-rcnn 中的 anchors 是在同一层feature-map上，可能具有不同的scale。Mutibox中作者没有明确提到priors的生成方式，只提到了priors需要满足的条件: 与bouding boxes的overlap超过0.5, 我揣测实际上这也是通过一个预训练的过程来实现的。

Overview

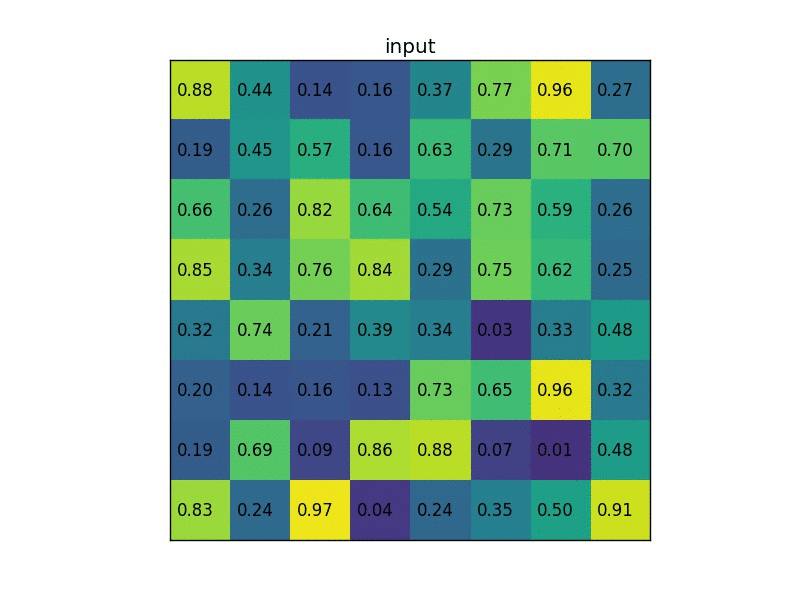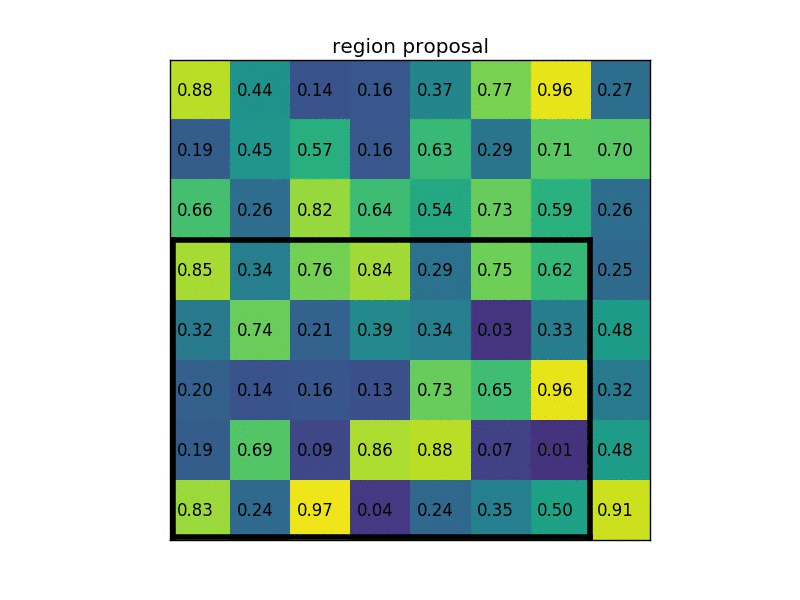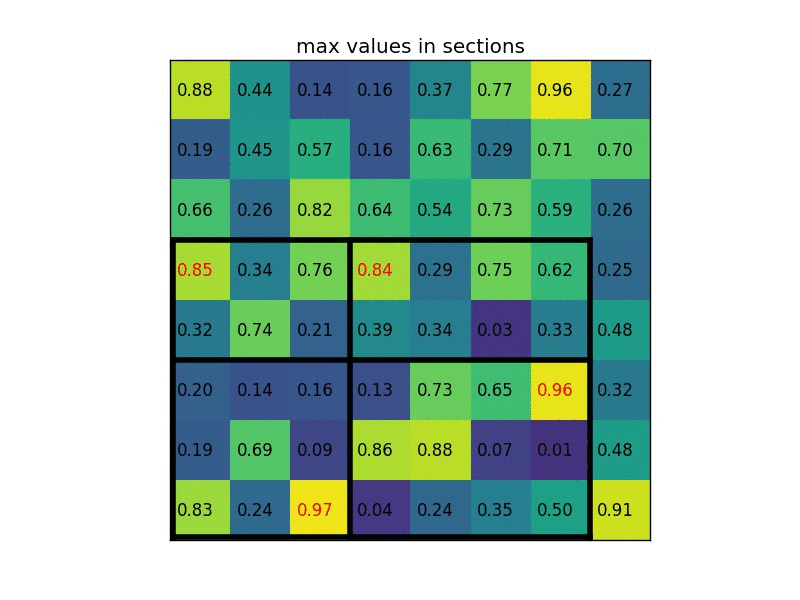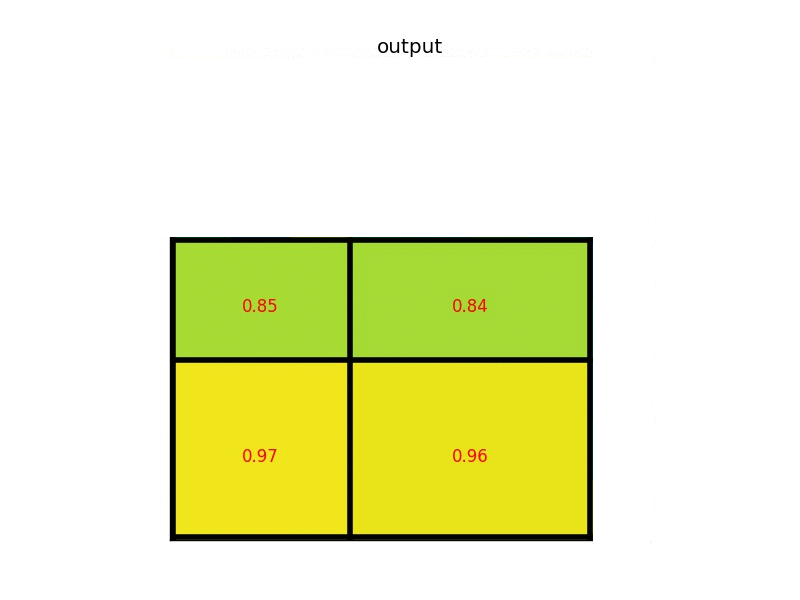
  基于motivation，作者设计了一个用于生成proposal(实际上output是对prior一一对应的slot)的网络，如下图(采用inception结构在不同尺度上预测objectness / locations)。从这个意义上来看，这一做法很类似于同时期Faster-RCNN提出的 RPN network。注意这一过程只预测 objectness(区分前后景)。通过这个网络结构预测出候选框后再选择加入分类器(post-classifier)进行分类。

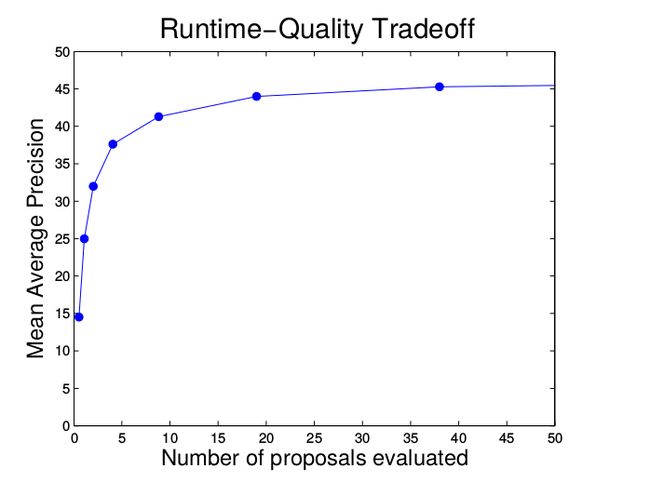
Speed Quality Trade-off

  通过objectness对候选框进行打分，改变evaluate的候选框的数量，实现 trade-off， 如下图

SSD

  Single Shot MultiBox Detector 2016 ECCV³很大程度上是受到上面MultiBox工作的启发，可以在速度大幅提升的条件下与faster-rcnn准确率相当，下面主要谈几点不同。

• SSD中采用的default boxes(priors)也是预先设定的，同样对应多个 feature-maps，但是不同于MultiBox(与ground truth IOU > 0.5), SSD中的priors则没有这个限制，这让 SSD可以适应更多的场景，也无需经过一个生成prior的预训练阶段。
• 匹配策略(matching strategy)不同于MultiBox, 即可以有多个default boxes匹配到同一个ground truth(e.g. 只要IOU > 0.5，这与后面faster-rcnn中实现的rpn策略是相似的)， MultiBox中则只选择IOU最大的那个prior。
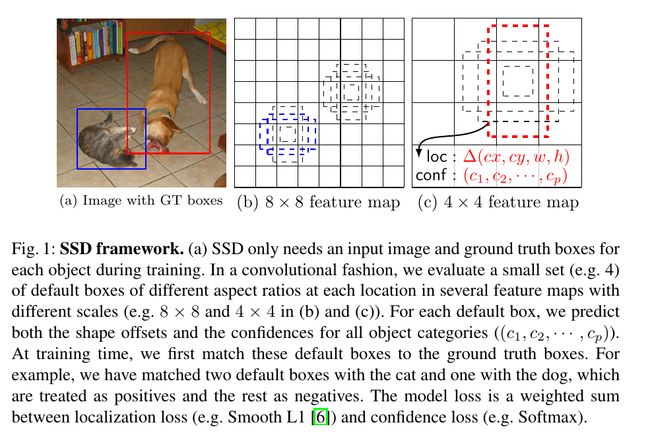
• SSD加入了classification loss, 在下图中可以看到对每个default box都会预测每个类别的置信度
• SSD 采用了 Smooth L1 localization loss(相对于L2 loss)

Network Overview

  如下图，backbone网络采用vgg-16, 在conv5_3之后加入若干的卷积层，在不同的尺度上预测类别信息和位置信息（相对于 default boxes的 offset)

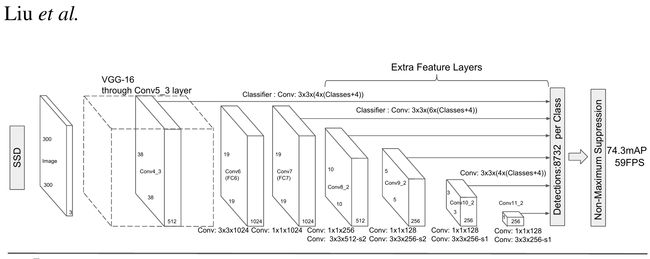
Drawback

  尽管网络结构中加入了不同尺度的信息，但是在实际中SSD表现出的一个很致命的短板是不善于检测小尺寸物体。后续的FPN⁴指出的可能原因是SSD预先经过了许多卷积层(直到conv5_3)，导致 high-resolution 的细节信息没有被利用到。

YOLOv3

   YOLOv3⁵是基于之前YOLOv1, v2提出的进阶版本，属于one-stage detector, 采用作者自己设计的darknet结构，下面的代码与图片大多来自 paperspace，表示感谢！

darknet官网

pytorch代码实现

Network Overview

# clone 到本地
git clone https://github.com/ayooshkathuria/YOLO_v3_tutorial_from_scratch
# 查看yolov3的网络结构
vim cfg/yolov3.cfg

  具体内容这里就不列出了，共有5种layer(更准确地说是pytorch中的nn.Sequential())

• convolutional layer: 卷积层，内部包含了BatchNormalization与Leakly ReLu激活函数
• upsampling layer: 上采样层: 为了检测小尺度物体，上采样以得到fine-grained的细节信息
• shortcut layer: 这个没啥好讲的，就是resnet中最简单的shortcut, 记录from信息表示从前面哪个层shortcut 过来
• route layer: 这个层会把两层的输出进行聚合
• detection layer: 进行检测的层，注意实现的时候由于要把不同尺度的检测结果(因为是对不同的feature map检测)concatenate到一起，所以需要先transform成 $$(batchSize\times grid\times grid\times num\_anchors)\times bbox\_attr$$的形式， 具体可以参考上面给出的代码链接

Interpret the output

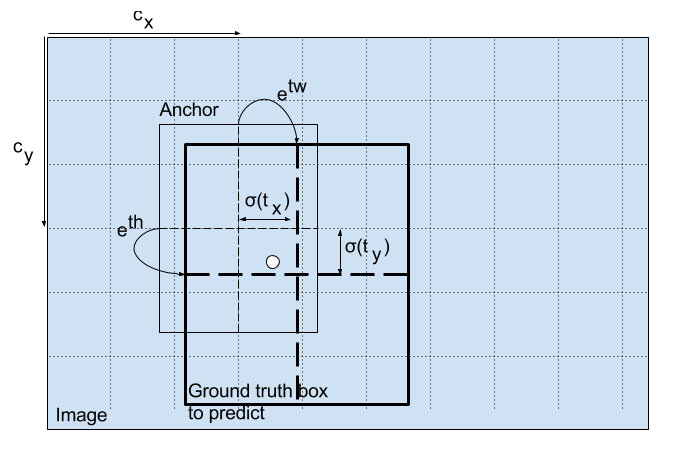
  如下图， 416 $\times$ 416 的输入经过 $stride=32$(后续再两个上采样进行detection) 的网络得到$13\times 13$的feature map，因此我们把原图划分为$13\times 13$个grids。$gri{d}_{(i,j)}$负责检测中心落在这个grid的物体(e.g. $gri{d}_{(7,7)}$负责检测小狗。

  再来看我们的输出，在depth的维度上，我们有$(5+nu{m}_{classes})$个输出，每个输出值的含义在上图中给出。值得一提的是预测的坐标形式，我们经过transform得到实际的在该feature map上的预测结果(即中心坐标，长宽信息), 变换如下，其中$t_x,t_y$刻画的是中心点在一个cell中的位置，需要先用sigmoid()归一化到0-1之间，否则就不在cell中了，$t_w$是预测的宽度信息，$p_w$是anchor的尺寸(需要先统一到feature map 上, divide by stride), $c_x$是每个grid's left-top的坐标信息，作为offset加上去

  在这个feature map完成检测后，我们再进行两次上采样，继续进行检测，操作类似

所以总共的预测结果数目是:$$SUM=(13\times 13+26\times 26+52\times 52)\times 3=10647$$
  这里$\times 3$是考虑到不同的aspect ratio，至于scale信息已经在不同的featture map中包含了，而要把10647个检测减少到1个，就是浩大的工程了(如NMS，置信度threshold等操作)

R-CNN

Overview

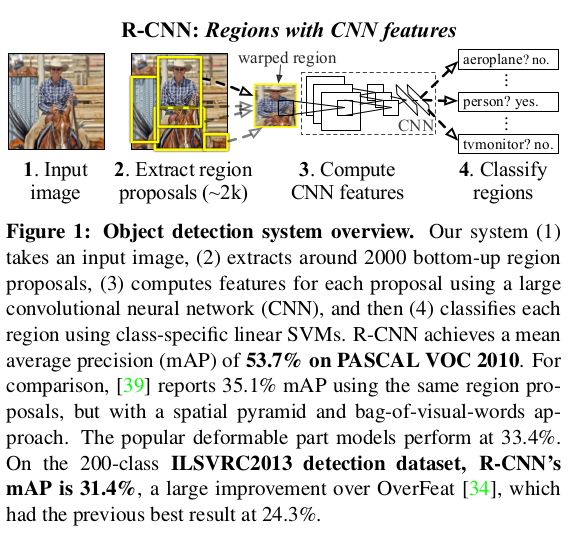
  R-CNN(2014 ECCV)⁶可以说是深度学习在目标检测方面的开山之作了，two-stage特征非常明显

1. 首先采用selective search 提取ROI
2. 提取的ROI需要先经过warp变换到同一尺寸(后续fc层的需要)
3. 将变换后的图像逐一输入到后面的分类层(实际上可以看成把先前保存在硬盘上的“ROI"输入分类层，转化成了一个分类问题)

Drawback

  速度瓶颈

• 从上面的步骤中就可以看出，因为每个ROI都要输入到分类层(如果有2000个ROI就要前向传播2000次，无疑是一个浩大的工程)。
• 此外，统一到相同尺寸也是一个费时间的活( 实际precision也会受影响)

SPP Net

Motivation

   SPPNet(Spatial Pyramid Pooling Network⁷)是针对上面R-CNN中分类器的输入尺寸必须要归一化到同一尺寸这一问题提出的, 可以把RCNN的速度提升20-100倍。Kaiming He 等人逆向考虑，既然需要尺寸统一，是不是可以加入网络层进行这一变换呢?下图给出了一般warp变换的流程(明显图像失真厉害) 和 SPP Network的流程

Network Overview

   在这个Pooling Layer中， bins的数量是恒定的，决定了不同尺寸的feature-map 经过池化得到的是尺寸是相同的。而每个bin的大小就是与图像尺寸成正比的了，具体实现可以参考后面的 ROI Pooling的代码，思想类似。

  作者设置了不同的bins数目，以便获得不同尺度的信息($1\times 1$的pooling也被称为global pooling，常常用来做防止过拟合或是weak supervision等工作。

Training Process

  训练过程中，作者首先用同一尺寸的输入训练网络(enable the multi-level pooling behavior)，然后在Multi-Size时将$224\times 224$ resize 到 $180\times 180$，保证内容信息基本相同，然后以epoch为最小单位交替训练网络(simulate the varying input sizes)。而Inference过程就没啥好说的了，任意尺寸输入直接用就是。

Fast R-CNN

Overview

  Fast-RCNN ICCV/2015⁷ 是针对上面工作进一步的改进版本，主要贡献:

• RCNN中提取的每个ROI都要经过前向传播，时间开销太大，因此Fast RCNN中选择先把输入图像前向传播若干层, 在此基础上再去用selective search提取ROI
• 提出ROI Pooling Layer为分类器提供统一尺寸的输入

ROI Pooling

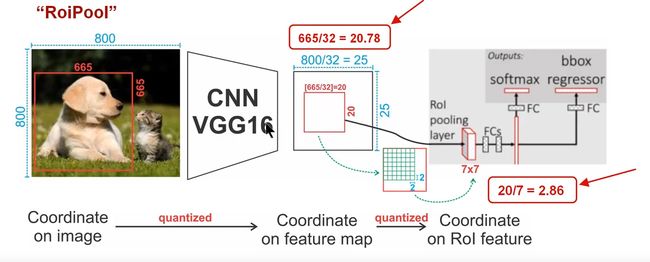
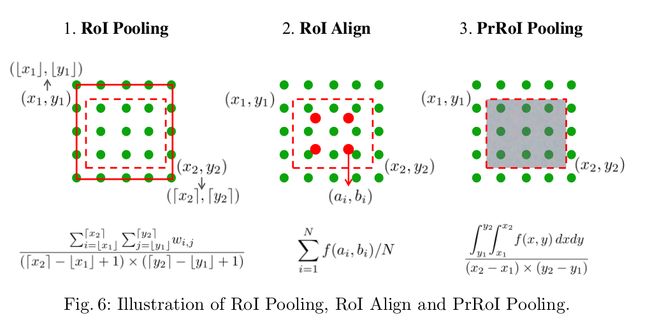
  注意在roi pooling过程中会有两次量化，第一次是由于ROI的坐标大多为浮点数，量化到所在feature map上时经过一次取整，这次误差可能看起来只有很小(e.g.如图0.78)，但是回传到原图($stride$=32 误差就很大了。第二次是由于pooling取整(e.g.如图 20/7不是整数,再次误差)，这个有后面的工作通过ROI Align和PrROI Pooling改进。
  这里附上动图和代码，分别来自Youtube, deepsense和jwyang

/* pw, ph分别代表池化层的输出位置， hstart, wstart等则代表输入的 pixel位置 */
/* 这里直接用暴力的方式遍历(4个for loop)与比较 */
for (ph = 0; ph < pooled_height; ++ph)
{
    for (pw = 0; pw < pooled_width; ++pw)
    {
        int hstart = (floor((float)(ph) * bin_size_h));
        int wstart = (floor((float)(pw) * bin_size_w));
        int hend = (ceil((float)(ph + 1) * bin_size_h));
        int wend = (ceil((float)(pw + 1) * bin_size_w));

        hstart = fminf(fmaxf(hstart + roi_start_h, 0), data_height);
        hend = fminf(fmaxf(hend + roi_start_h, 0), data_height);
        wstart = fminf(fmaxf(wstart + roi_start_w, 0), data_width);
        wend = fminf(fmaxf(wend + roi_start_w, 0), data_width);

        const int pool_index = index_output + (ph * pooled_width + pw);
        int is_empty = (hend <= hstart) || (wend <= wstart);
        if (is_empty)
        {
            for (c = 0; c < num_channels * output_area; c += output_area)
            {
                output_flat[pool_index + c] = 0;
            }
        }
        else
        {
            int h, w, c;
            for (h = hstart; h < hend; ++h)
            {
                for (w = wstart; w < wend; ++w)
                {
                    for (c = 0; c < num_channels; ++c)
                    {
                        const int index = (h * data_width + w) * num_channels + c;
                        if (data_flat[index_data + index] > output_flat[pool_index + c * output_area])
                        {
                            output_flat[pool_index + c * output_area] = data_flat[index_data + index];
                        }
                    }
                }
            }
        }
    }
}

Back Propogation

  反向传播的代码就不列出，在jwyang的repo中同样可以找到，但是cuda编程比较复杂，我还没学过 。 其公式如下，注意只有池化后的pixel $y_j$在池化时用到了前面的 $x_i$才会传回梯度
$$\frac{\partial L}{\partial x_i}=\sum _r\sum _j[i=i^{\ast }(r,j]\frac{\partial L}{\partial y_j}$$

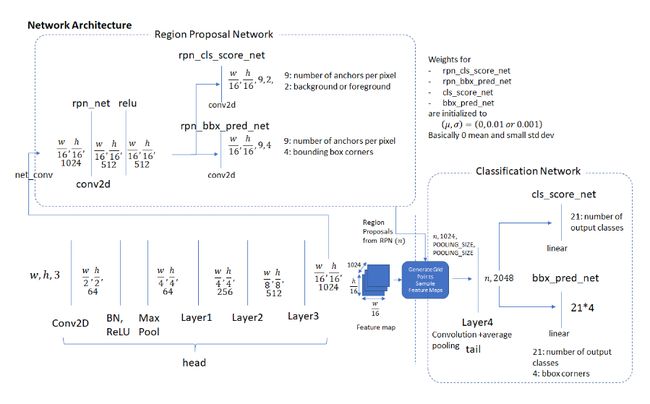
Faster R-CNN

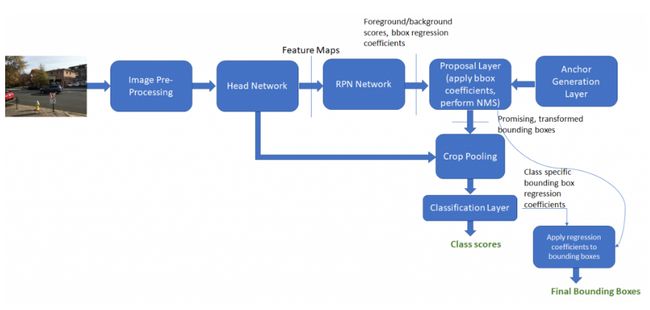
  Faster R-CNN 2015/NIPS⁸ 是Fast RCNN的进一步改进版本，简单来说就是RPN + Fast RCNN(同时期MultiBox v2提出可学习的提取ROI方式)，这里强推一个基于pytorch的实现版本，来自jwyang，写得真是很好!
  下面我参考blog具体谈谈整个网络结构(之前的RCNN和Fast RCNN都没细说 )， 结合代码体会效果更佳哦~
  感谢(credit)来自ankur6ue的图，讲的很清楚(虽然是英文的可能有语言障碍…)

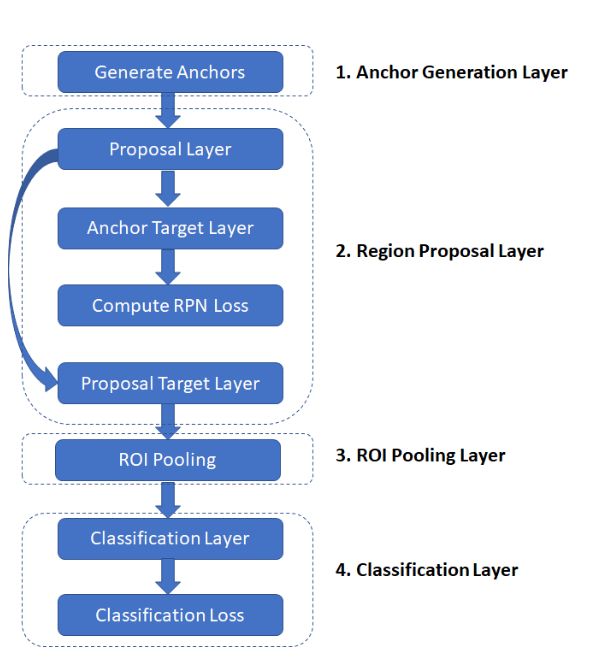
Network Architecture

  网络的结构如图所示，各层之间的关系大概如下:

• Anchor Generation Layer产生anchors，这些anchors会提供给proposal layer和anchor target layer
• Proposal Layer主要做的工作是把RPN预测的box regression信息作用到前一步的anchors上，这一步得到的就是proposals，然后根据设定的超参数(包括前后景比例，PRE_NMS_NUM, POST_NMS_NUM, 根据ranking选择排在顶部的候选框，由此限制候选框数量…
• Anchor target Layer主要产生的是用来训练RPN的信息。怎么产生的? Anchor target Layer把第一步产生的anchors和groud truths比较，通过IOU阈值标定每个anchor的前后景类别。这一层我们得到anchor targets和anchor labels。什么是anchor target?，简而言之就是我们的anchor需要通过怎么样的变换才能到ground truth的位置, 这个anchor target和我们RPN现阶段预测的box_pred运算得出loss值，注意其中回归的loss值是L1 smooth和class-agnostic的
• Proposal Target Layer: 当我们的RPN已经训练得不错的时候，我们Proposal Layer得到的proposals应该已经有一定的质量了，这个时候proposal target layer把这些proposals和ground truths比较，得到proposal_targets **什么是proposal targets **类似于上面的anchor targets，这个和最终回归器的输出box_pred做L1-smooth差得到我们训练最后回归器的loss,注意这里的回归loss是class-specific的(不同于one-stage一般是class-agnostic)。至于分类就没啥好说的，都是softmax和交叉熵。

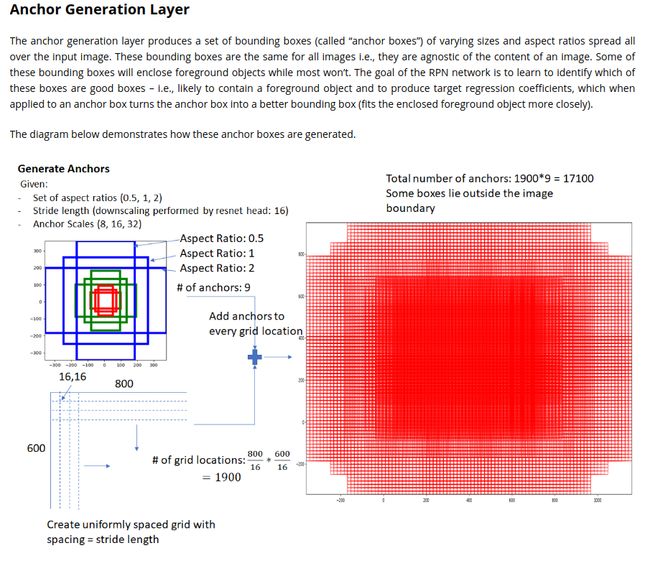
Anchor Generation Layer

  不同于之前的SSD和MultiBox, 由于anchors是在同一个feature map上的，我们每个grid有9个anchors, 3个长宽比，3个尺寸参数(后面 使用了FPN后就可以不用这个了)

Anchor Target Layer

  我们在给anchor打类别的时候，有三种。$-1,0,1$, 分别代表"don’t care", 背景， 前景。这边用到超参数RPN.NEGETIVE_THRESH(重叠小于该参数时设为背景，设为0.3), RPN.POSITIVE_THRESH(重叠大于该值，设为前景，0.7)。在两个值之间的，我们标记为don’t care。总之, 选择策略如下:

• 若某个anchor和某个ground truth的IOU在所有anchors中是排最大的，则不论该IOU是否超过阈值，均标记为前景
• anchor和grouth truth的IOU超过阈值(e.g. 0.7)
• 若前景占比大于某个阈值(e.g. 0.5),我们就随机选择一些打上-1的标签

Inference

R-FCN

Motivation

  首先我们回顾一下分类任务(classification)和检测任务(detection)对于特征的不同需求。分类网络大多是translation invariant(位置不敏感性), 因此这几年的主流网络(e.g. resnet, inception等除了最终分类器外都会使用卷积层(卷积层是translation invariant), 但是检测任务要求是translation variant(位置敏感的)，怎么办?
  为了解决这一问题，Kaiming He 通过给faster-rcnn加入roi-pooling打破了这种位置不敏感性，但是带来了新的问题，即ROI-wise network部分计算量大，因为每个ROI都要经过若干曾的卷积运算

主流two-stage网络大致可分为两个step

• 在ROI网络层之前的全卷积网络
• ROI之后的网络，我们叫ROI-wise network

  总地来说，问题就是:

• 全卷积 + ROI-wise的fc $\to$translation-invariant, 不适合detection task, 准确率低
• 保留ROI-Pooling,其前后都有卷积层$\to$ 增加了ROI-wise网络的深度，但是计算量大，速度慢

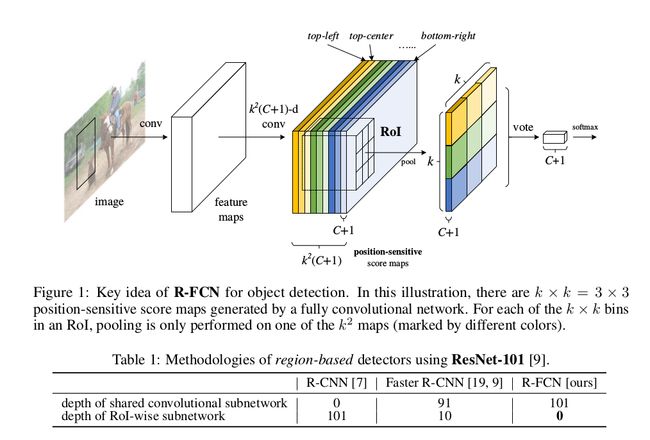
  基于此，R-FCN 2016/NIPS⁹提出了解决方式，全卷积，ROI-Wise Network无计算量，即没有层的基础上提出了position-sensitive score maps来保证translation variant

Overview

  网络结构如下图，可以看到R-FCN避免了roi-wise的复杂运算，下面阐释一下这个position-sensitive score maps的概念
  如图，假设第一部分最后一个卷积层的输出的维度是$H\times W\times C_{in}$, 那么我们通过一个same-padding,filters数目为$k^2(C+1)$的卷积层(C代表类别数量，+1是考虑到背景，得到$H\times W\times k^2(C+1)$的输出，如图所示，这里的$k$是人为指定的(e.g. 如图$k=3$)，论文中指出: $k^2$中的每个channel可以看成分别对应ROI的top-left,top-center...等9个位置。当给定一个类别时，我们先对$k^2$中的每个map做postion-sensitive ROI pooling,公式如下:
$$r_c(i,j|\Theta )=\sum _{(x,y)\in bin(i,j)}{z}_{i,j,c}(x+x_0,y+y_0|\Theta )/n$$ 然后我们对这$k^2$个pooling的结果做一个voting，得到$dim=C+1$维度的$vector$，即为每个类别对应的置信度

  为何可以$k^2$个可以看成是左上角，左下角这类的区域? 一方面，注意到position-sensitive pooling是对$k^2$中的每个区域分别进行pooling，即每个score map对应一个子区域。另一方面我个人认为因为卷积层的depth维度实际上是对同一个region位置不同信息的的挖掘，这种左上角，左下角 .etc 更像是一种assumption,但是是挖掘不同信息的，所以voting也可以make sense，这点还没弄清，求高手指点:-)

Visualization

FPN

Motivation

  Feature Pyramid Network CVPR/2017⁴提出了特征金字塔的model， 实际上图像或是feature map的scale一直是一个备受关注的问题，我们之前提到的MultiBox和SSD都有不同尺度feature maps上的default boxes, 还有Faster-RCNN中直接指定anchors大小差异的scale, 而传统的Image Pyramid对运算来说来说是很大负担，FPN希望通过特征金字塔学习到更多不同尺度上的信息，改善模型表现。

Network Overview

  两个pyramid,一个bottom-up, 一个top-down，通过横向连接拼接在一起

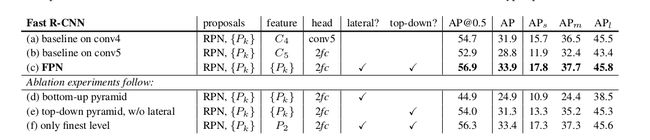
Ablation Experiments

  如下图，作者在论文中指出了横向连接lateral connection和上采样upsamling的必要性。简单来说:

• bottom-up pyramid中的各层有很大的语义差semantic gap，如果没有top-down的encrichment, 结果会很糟糕(如图)。
• 而top-down的信息由于经过了太多的sampling(又是下采样又是上采样)，所以位置信息不太行，就需要lateral connection来丰富细节的位置信息

Code Implementation

  可以参考jwyang基于pytorch的实现，虽然代码还存在一些bug，但是用来学习足够了，如下$[c1,c2,c3,c4,c5]$是bottom-up的金字塔，对c5我们使用self.RCNN_toplayer(实际上是一个$1\times 1$的卷积层)进行降维, 然后再自顶向下build我们的金字塔。注意$[p1,p2,p3,p4,p5]$分别对应$[c1,c2,c3,c4,c5]$, 而提供给RPN的还会多一个$[p6]$，即对$[p5]$做max-pooling得到的层(论文中提到covering a larger anchor scale of 512^2)。此外，代码中的RCNN- smooth是加入一个$3\times 3$的卷积层，用来防止aliasing effect(大概是信号混叠效应啥的…)

# feed image data to base model to obtain base feature map
# Bottom-up
c1 = self.RCNN_layer0(im_data)
c2 = self.RCNN_layer1(c1)
c3 = self.RCNN_layer2(c2)
c4 = self.RCNN_layer3(c3)
c5 = self.RCNN_layer4(c4)
# Top-down, top layer for dimension reduction, the RCNN_toplayer only contains one convolution layer
p5 = self.RCNN_toplayer(c5)
p4 = self._upsample_add(p5, self.RCNN_latlayer1(c4))
p4 = self.RCNN_smooth1(p4)
p3 = self._upsample_add(p4, self.RCNN_latlayer2(c3))
p3 = self.RCNN_smooth2(p3)
p2 = self._upsample_add(p3, self.RCNN_latlayer3(c2))
p2 = self.RCNN_smooth3(p2)

p6 = self.maxpool2d(p5)

# rpn has one more feature map
rpn_feature_maps = [p2, p3, p4, p5, p6]
mrcnn_feature_maps = [p2, p3, p4, p5]

rois, rpn_loss_cls, rpn_loss_bbox = self.RCNN_rpn(rpn_feature_maps, im_info, gt_boxes, num_boxes)

  我们把rpn_feature_maps传入rpn网络，得到不同尺度大小的rois，再根据论文中给出的如下公式为每个roi设定level, 做roi pooling，传入分类和检测器，输入结果~
$$k=\lfloor k_0+lo{g}_2(\sqrt{wh}/224)\rfloor (e.g.k_0=4)$$

Mask R-CNN

Introduction

  Mask-RCNN 2017/Kaiming He¹⁰一方面根据同时期其它的一些work做了一些改进,在ResnetXt[^16] + FPN作为backbone网络的Faster-RCNN上再加了一个用于instance segmentation的branch，由于我不是做分割的，这里就不谈了，主要说一下ROI-Align

ROI Align

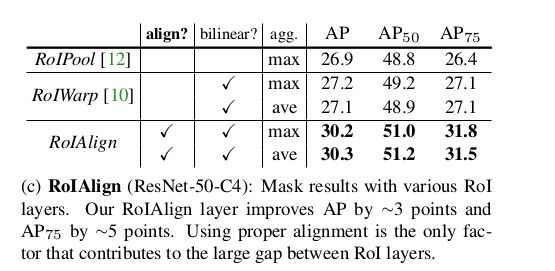
  之前已经提到，ROI Pooling中的两次量化带来了很大的误差，由此Kaiming He 提出了下面的ROI Align解决misalignment的问题，在准确率上提升了不少
  如图所示, 虚线代表的是feature map, 黑色实线代表我们的ROI，我们首先通过双线性插值的方式计算出采样点(黑色圆点)处的值(基于feature map上坐标为整数的值)，再对每个bin内的四个采样点做pooling得到我们的结果

  如图所示，roi align对准确率提升有很大帮助

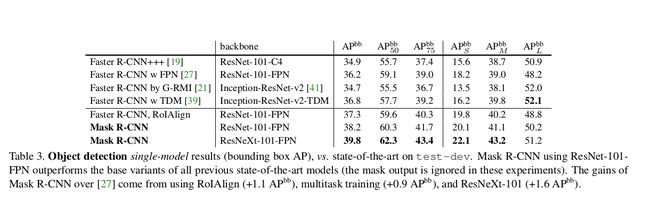
Performace

  在Object Detection上准确率有了很大的提升，有力的benchmark和baseline

NMS

Motivation

  NMS(non-max-suppresion)早在前深度学习时代就有了，一般我们现在用的是standard NMS(又叫 Greedy NMS)。NMS是为了解决detection pipeline中的检测冗余。在上面YOLOv3中我们提到过要把10647个检测减少到1个…很大一部分就是通过NMS完成的。
  作为Inference阶段一种post-processing方法， 经典的NMS一般是这样的: 将每个image中所有的检测(detections)按置信度(confidence)排降序，取置信度最高的那个detection，然后把所有detections中与这个detection的IOU大于某个阈值(threshold(e.g. 0.5)的结果都丢掉…以此类推…后面为给出伪代码，这里我们看一下一个比较经典的python代码实现

def nms_cpu(dets, thresh):
    """
    perform nms class-wise
    :param dets: N * 5 where N is the batch size
    :param thresh: threshold to discard overlapped detections
    :return: post-processing result
    """
    dets = dets.cpu().numpy()
    x1 = dets[:, 0]
    y1 = dets[:, 1]
    x2 = dets[:, 2]
    y2 = dets[:, 3]
    scores = dets[:, 4]

    areas = (x2 - x1 + 1) * (y2 - y1 + 1)
    # sort and get the order
    order = scores.argsort()[::-1]

    keep = []
    while order.size > 0:
        i = order.item(0)
        keep.append(i)
        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])

        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        ovr = inter / (areas[i] + areas[order[1:]] - inter)

        inds = np.where(ovr <= thresh)[0]
        # shift the order 
        order = order[inds + 1]

    return torch.IntTensor(keep)

Soft NMS

Motivation

Github代码

  原生的NMS似乎太过严格，只要overlap大于一定阈值就丢掉检测框，这在物体密集场景(如人流)中可能会带来较低的召回率。基于此soft nms 8/2017¹¹ 提出用一行代码改善目标检测的性能，伪代码如下，实际上是对overlap大于一定阈值的检测重新打分(降低他们的置信度，而不是直接discard)

Score Function

  实际上NMS可以看成是soft nms的特例，NMS的score函数如下

  对于soft nms来说，重叠更大的检测越有可能是fasle positive，分数自然应该减少得更多，下面这种decay函数似乎是比较符合直觉的

  但是上面的函数在IOU刚好到N_t的地方会有一个跳跃，理想的情况是能找到一个连续的函数满足条件，即减少所有剩余框的置信度，使用Gaussian函数如下:

Learning NMS

Motivation

  soft-nms有一个显而易见的好处，就是只在Inference阶段使用，且时间开销小让它可以被广泛应用。但当今的trend是端到端的深度网络，我们往往希望可以做一个可学习的，自适应的NMS算法机制。基于此，Learning non-max-suppresion 2017¹²提出了GossipNet用来做post-processing。

Related Work

• 聚类检测(Clustering Algorithms)，很少能在表现上超过GreedyNMS
• 像素单位的检测(Linking detections to pixels)，需要额外的监督信息(如分割标注等), 而本文提出的NMS方法无需其它的监督信息
• 共同出现(co-occurence)，这个问题更复杂，因为我们要处理的是多个检测(后面的Relation Network是相关的探索，我个人觉得是比较有意思
• 端到端(end-to-end)的网络。有人尝试把GreedyNMS加入到训练过程中，但是依旧不可学习(non-learnable)。有人尝试直接让网络生成稀疏(sparse)的检测，但是出于某种原因(比较复杂，不详谈)，post-processing依旧需要。而本文提出的则是一个更端到端的网络结构，不需要post-processing或者是GreedyNMS

  总而言之呢， Learning NMS提出的是无需图像信息(即输入是bouding boxes而不含feature信息，无需任何的post-processing的pure-NMS网络结构

A future without NMS

  展望一下完全端到端而没有需要手工设计的未来世界，作者指出了两个很重要的要素(ingredient)

• 一个惩罚重复检测的损失函数(loss for multiple detections for one object)
• 相邻的检测需要同时处理(joint processing), 其实上也是为了挖掘相邻检测之间的关系(这样detector就可以知道是否有重复检测了)

Doing NMS With Convnet

  作者首先的一个思路和soft nms比较相似，就是把NMS作为一个重新打分的过程(rescoring)，而不是直接抹杀候选框。重新打分后的候选框直接送到evaluation的过程。

Loss

  论文中采用的匹配规则是: 每个object只能被匹配一次，多余的detection被计为false positive, 由此我们定义$$y_i=\{-1,1\}$$ 若detection $d_i$成功匹配，标记为1，否则标记为-1。用$s_i=f(d_i)$表示打分函数。 在此基础上用一个binary loss 来训练我们的网络。
$$L=\sum _{i=1}^N{w}_{y_i}(log(1+exp(-s_i{y}_i))$$
在多类别场景中，我们只把detection匹配到对应的类别上。注意公式中$w_{y_i}$是用来平衡类别之间的检测差异的(即保证每个类别地位相同)。经过训练，我们就保证了没有成功匹配的detection的分数低，成功匹配的detection分数高

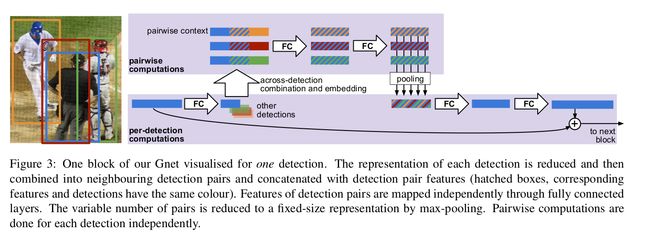
Chatty Windows

  为了有效地最小化上面定义的loss,作者设计了Gossip Net(GNet)，总体结构如上面的Figure2。注意我们这里输入的detections的信息，是不含图像信息的，即只有$|bo{x}_{attrs}|$个维度，我们先把这些输入到三个FC全连接层后(根据论文，其输出维度为128)，再把结果作为block的输入，每个block的结构如Figure3所示。

  在我们的block中，detection先被fc降为到$c=32$的维度，然后把这个特征向量和它邻居(e.g. IOU > 0.2) 的特征向量拼接在一起， 构成$l=2c+g$维度的向量。举个例子, $(d_i,d_j)$拼接在一起，每个detection各有$c$维度， 剩下的$g$维度是用来描述两个detection的关系信息的，包括:

• IOU
• $x,y$方向上归一化后的$l2$距离
• 宽度和高度上的尺寸差异(e.g. $log(w_i/w_j)$)
• 宽高比的差异, $log(a_i/a_j)$

  考虑包含一张图片中所有检测的mini-batch, 设其维度为$n\times c$, 表示有$n$个detections， 如果对于检测框$d_i$有$k_i$个相邻框，那么我们在配对的时候可以得到$K\times l$的矩阵，其中$K={\sum }_{i=1}^n(k_i+1)$, $l$是上面定义过的。但是这样的表示会带来一个问题，即不同检测框的邻居数量差异可能很大，为此我们对每个检测框所有的邻居做一个global max pooling，就得到了$n\times l$的矩阵，然后结果经过两个$fc$层后输入给下一个block…以此类推，最终最后一个fc层将输出我们对于所有检测框新的scores

Remarks

  作者提供的方法实际上没有用到图像的信息，那么在未来end-to-end的detector中，我们必须要做的一个工作就是怎么把图像信息融入进去……(left for future work)

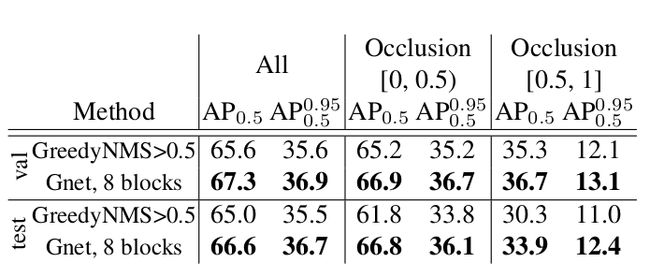
Experiments

IoU-Net

Motivation:

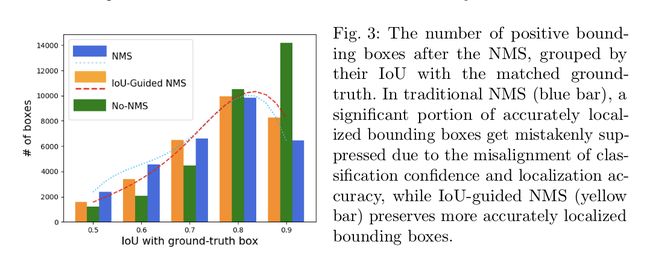
  GreedyNMS有一个显而易见的问题，就是定位准确度(localization confidence)和分类准确度(classification confidence), 即我们分类置信度高的定位效果不一定好，而实际中我们往往是需要保留更准确的检测框的，如下图:

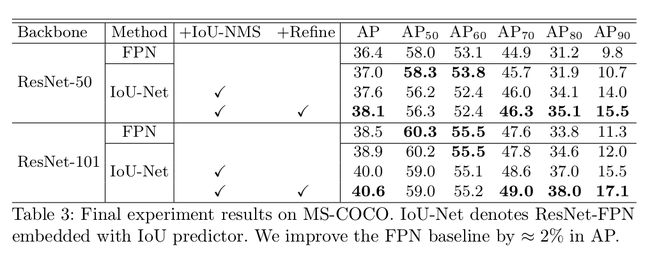
  基于此，旷世科技在Acquisition of Localization Confidence For Accurate Object Detection 7/2018¹³一文中提出了Iou-guided NMS和以预测IOU值为目标函数的IoU-Net，旨在解决这一问题。

Related Work:

  GossipNet¹²以及一些其它工作提出了端到端的NMS变体，但是带来的一个问题就是计算量。
  作者分析了Pearson系数，发现IOU与分类准确率似乎没有关系

  如下图，最右边一列IOU > 0.9中我们可以发现NMS的数量要比Non-NMS少将近一半，说明有很多定位准确的检测被NMS扼杀了

Optimization-Based Vs Regression Based

  作者把IoU-net的输出(IoU predicted)作为定位置信度的表征，这一表征作为IoU-Net的训练目标函数，这种方法作者称之为optimization-based。将它与一般regression based的方法对比后，我们可以发现，如果我们加入很多regression层(即不断地去优化坐标信息)，AP是下降的，如下图二的可视化结果可见，IOU不断减小。由此作者佐证了IoU-Net的优势所在。

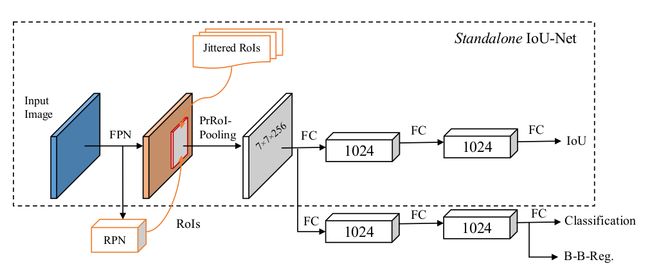
IOU-Net

  IoU-Net的结构如下图，其实是在PrRoiPooling的输出结果后加了一个分支，用来预测IoU值作为定位置信度的表征。这边值得一提的是IOU-Net的训练过程:

• 用$\{B_1,B_2,\cdots B_n\}$表示一张图片中的所有ground truth，我们首先对这样标注框进行随机变换(transform)，得到$\{B_1^{{}^{\prime }},\cdots ,B_n^{{}^{\prime }}\}$
• 前面输出的ROI会匹配到一个标注框，我们记为$C$, 这个时候我们把集合$B_i^{{}^{\prime }}$中所有和$C$ 的IOU < 0.5的移除
• 对剩余的$B_i^{{}^{\prime }}$进行随机采样(uniformly), 得到的IOU值即作为我们的预测值

   这样处理的一个好处就是可以增加我们模型的鲁棒性

IOU-guided NMS

  上面我们的IOU-Net输出了一个预测的IOU值，我们以这个值为依据来做IOU-guided NMS。顾名思义，和NMS不同的是，我们是依据IoU predicted by IoU Net 作为排序依据的。举个例子，取出预测IOU值最高的框，如果剩余框中有的框和该框IOU超过阈值，则抹杀之，并更新先取出的框的分数，具体见下面伪代码。

Bounding Boxes Refinement

  检测任务中有一步是对输出检测框进行调整，目标如下:
$$c^{\ast }=\text{arg}\underset{c}{\min }crit(\text{transform}(bo{x}_{det},c),bo{x}_{gt})$$
  一般意义上通过深度前馈网络进行迭代的regression based方法对输入比较敏感, 而且会产生前面所说的退化问题。这里作者用以IOU为目标函数对bouding boxes进行修剪，即更新检测框坐标值(目的是优化IoU-Net输出的IoU值)，后面的实验结果也证明这种方式的有效性

PrRoiPooling

Github代码

  作者指出ROI-Align方式不是连续可导的，且采样点的数目N不能自适应bin的大小，因此提出了Precise ROI Pooling的方法: 用$w_{i,j}$表示feature map上位置为$(i,j)$的值(注意是离散的)。然后我们用双线性插值的方法计算出bin中任意位置$(x,y)$的值(连续化): $$f(x,y)=\sum _{i,j}IC(x,y,i,j)\times w_{i,j}$$ 其中$IC(x,y,i,j)=max(0,1-|x-i|)\times max(0,1-|y-j|)$是插值系数。接着，对每个bin内的值进行积分得到结果
$$ProPool(bin,\mathcal{F})=\frac{{\int }_{y_1}^{y_2}{\int }_{x_1}^{x_2}f(x,y)dxdy}{(x2-x1)\times (y2-y1)}$$

Experiments

Softer NMS

Github

Motivation

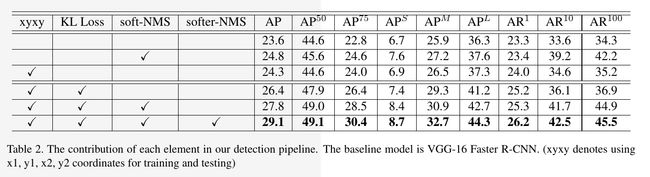
  softer nms 9/2018¹⁴是Face++的另一篇论文。不同于IoU-Net, 这篇论文从概率的角度给出了数学推导，提出了一种新的用于位置回归的损失函数，把vgg-based faser-rcnn在coco上的准确率从23.6%提升到了29.1%, 把Resnet 50 FPN based faster-rcnn准确率从36.8%提升到了37.8%。

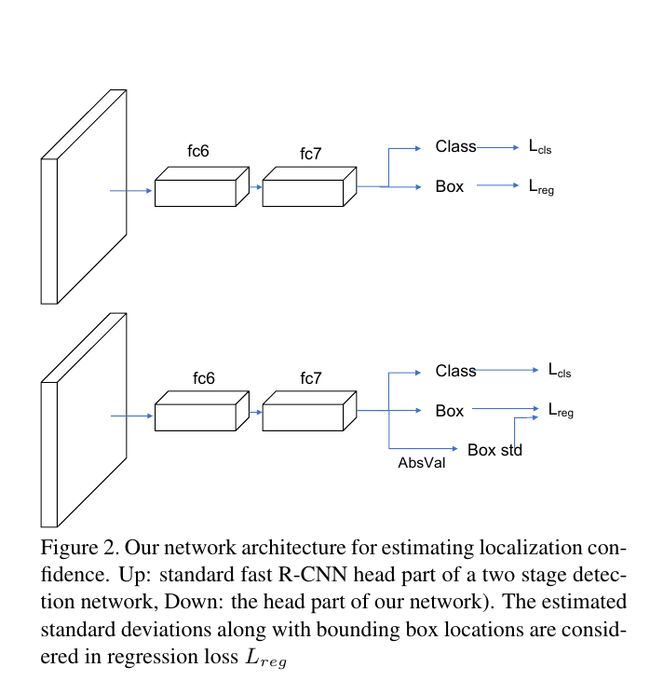
Network Overview

  网络结构如下图，加了一个分支预测定位置信度$\sigma$(数学分析在下面), 这边采用绝对值(absval)替代relu防止大多输出变为0。

Deduction

  网络结构如图所示，在预测回归信息的同时加了一个分支以预测定位置信度$\sigma$, 即我们可以把预测的bounding boxes看成是正态分布,$$P_{\Theta }(x)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{(x-x_e{)}^2}{2{\sigma }^2}}$$
  $x_e$表示预测的坐标值。$\sigma$越小代表我们对我们的预测越有信心。
  再来看我们的groud_truth的分布，实际上也可以看成是正态分布，不过由于其完全确定，实际上是狄利克雷分布, 满足$$P_D(x)=\delta (x-x_g)$$
  这个时候作者定义回归损失函数$L_{reg}=D_{KL}(P_D(x)||P_{\Theta }(x))$，即为两个分布之间的KL散度。直观来看，为了让两个KL散度最小，两个分布应当越接近。作者的推导如下:

  这边等式(7)作者应该是存在笔误，从等式(5)对$\sigma$求导，得到的结果应当是:
$$\frac{d}{d\sigma }(D_{KL}(P_D(x)||P_{\Theta }(x))=-\frac{(x_e-x_g{)}^2}{{\sigma }^{-3}}+\frac{1}{\sigma }$$如此看来$\sigma$应当存在最优解，即
$$\sigma =|x_e-x_g|$$
所以我们应当是期望$|x_e-x_g|$与$\sigma$一同减小，相当于bias和variance同时减小(个人觉得这边作者在原文的表述存在一些问题)
  考虑到刚开始训练的时候$\sigma$小，引起梯度爆炸，我们实际训练的时候是用$\alpha =\frac{1}{{\sigma }^2}$

Algorithm

  如图，实际上是对分数置信度较高的检测框做了调整(即取了周围几个框和自身的加权平均，这其实上是合并框比较符合直觉的)

Experiment Results

   如图可以发现soft-nms + softer-nms可以获得相当不错的表现

Relation Network

Motivation

  Relation Network 6/2018¹⁵近年来，目标检测任务大多还是对单个物体逐一进行处理，对于多物体之间的关系挖掘较少。加之NLP中的attention机制逐渐被运用到视觉任务中，本文作者基于自适应的注意力机制(adaptive attention module)，提出了一种关系模型，希望通过一张图片中不同物体的外形特征和几何关系对这些物体的关系进行建模，实现第一个彻底端到端的detection pipeline
  RM也可以用到去重任务中(NMS), 之前提出的GossipNet¹² 需要很深学习网络，也因此带来了繁重的计算量，而RM则一定程度上避免了这个问题

Related Work

• Object Relation Post-processing早在前深度学习时代就有工作指出通过多个目标之间的关系对目标进行重新打分(如哪些目标不会同时出现等)
• Sequential processing有工作尝试用LSTM和SMN对物体的关系进行建模，在这种模型里，先一步被检测出的目标有助于下一个目标的检测

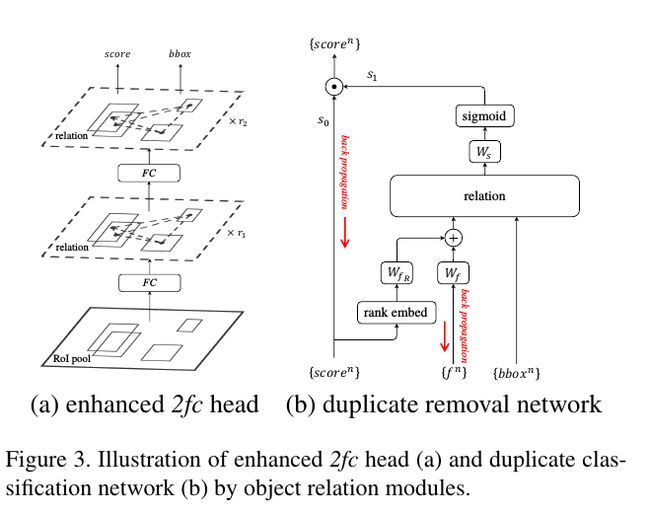
Object Relation Module(RM)

  我们首先回顾一下最基本的attention模型， 用$q\in R^{d_k}$表示query, $K\in R^{n\times d_k}$表示一个个key拼接在一起的矩阵。$V$表示$K$对应的values然后我们还是用点积(dot product)来刻画激活程度(就像我们在可视化某一层feature map时的做法一样)。$$v_{out}=softmax(\frac{\text{q}{K}^t}{\sqrt{d_k}})V$$
  回到我们的RM上，定义集合$\{f_A^n,f_G^n{\}}_{n=1}^N$表示我们的目标集合，其中下标为$A$的表示维度为$d_f$的外形特征，其具体内容依任务而定。, $f_G$表示几何特征(dim=4,即各个坐标值)。那么整个目标集合对于某一个目标$n$的关系就可以表达为:$$f_R(n)=\sum _m{w}^{mn}(W_V\cdot f_A^m)$$
  表示的实际上是对各个经过线性变换的外形特征做加权平均。其中$w_{mn}$(attention weight)表示的即为受其它目标的影响程度，依据外形权重关系和几何权重关系计算，公式如下
$$w^{mn}=\frac{w_G^{mn}exp(w_A^{mn})}{{\sum }_{k=1}^n{w}_G^{kn}exp(w_A^{kn})}$$
  外形权重(appearance weight)取决于$m,n$外形特征的相似度，如下
$$w_A^{mn}=\frac{\text{dot}(W_K{f}_A^m,W_Q{f}_A^n))}{\sqrt{d_k}}$$
  $W_k$和$W_Q$矩阵的作用和上面的$K$, $V$相似，分别表示keys和query的values，把$f_A$投影到子空间来匹配相似度。
  值得一提的是$w_G^{mn}$的计算，作者先把$f_G^n,f_G^m$用一个相对特征来表示，从而增强对尺寸变换的鲁棒性，即$(log(\frac{|x_m-x_n|}{w_m}),log(\frac{|y_m-y_n|}{h_m}),log(\frac{w_n}{w_m}),log(\frac{h_n}{h_m}){)}^T$，然后再把这个4维特征嵌入到高维的表达(比较复杂, 计算正余弦啥的，具体可参考论文)，高维表达经过$W_G$变换后取了relu。公式:
$$w_G^{mn}=max(0,{ϵ}_G(f_G^m,f_G^n)$$
  经过这一步之后，我们就可以回到上面计算出$f_R(n)$了，下一步就是把所有的关系聚合，对原先的目标特征进行调整，如下(为保证维度匹配，通过$W_V^r$进行变换
$$f_A^n=f_A^n+concat(f_R^1(n)+f_R^2(n)+\cdots +f_R^{N_r}(n))\text{for all n}$$

Instace Recognition & Duplicate Removal

  Instance recognition 我们用RM + fc(RM模块不会改变维度)来取代原先的fc层，输出分数和坐标值。
  Duplicate Removal如Figure3(b)我们在这个网络中有两个分数，其中$s_0$是上一层(Instance Recognition)的输出, 而$s_1$用来表示一个检测是正确匹配还是多余的(duplicate, 这里采用的规则是一个gt只能被一个检测匹配，多余的我们标记为duplicate)。这边作者用到的一个trick是rank feature，即通过分数排序，量化到$1,2,\cdots ,N$，再嵌入到高维表达(类似于上面)。在这一步中，每个检测都有1024个features，score，boxes等属性(其中features 和score融合得到$f_A$特征作为RM的输入。

Training Remarks

$$Loss=-log(1-s_0{s}_1)$$
  实际上，为什么这个简单的交叉熵可以很好地work呢? 可以预见的是大多数的检测的$s_0$分数都会趋近于0，对这部分来说, $\partial L/\partial s_1=s_0/(1-s_0{s}_1)$的值也会很小，所以不会影响优化过程。网络会自动去专注于那些真正多余的检测(real duplicate)，这其实上和Focal Loss的思想很像。
  此外，在完全端到端训练模式中(即把上面的instance recognition和duplicate removal结合起来)，损失函数会不会如我们期望的那般收敛呢?
  直观来看，两个tasks之间似乎存在着矛盾，instance recognition更希望每个检测结果都能被打到很高的分数，但是duplicate removal却希望只有一个检测结果的分数高。但是作者发现在实现时两个网络都能很快的收敛，说明instance recognition网络复杂输出高的$s_0$,而duplicate removal负责给不合理的检测打上很低很低的$s_1$，这样来看， Loss 也就下去了。

Experiment Results

  从图中明显可以看到，端到端的结果有改善

文末顺便提一句，上面的大多代码都是fork detectron实现的，强烈推荐clone这个facebook开源的做目标检测的框架(目前已经有20000个stars)

---

Reference

七月在线
知乎mask r-cnn
知乎R-FCN
ankur6ue’s Faster RCNN blog
ayooshkathuria’s YOLO_v3 tutorial
jwyang(大哥代码写得超好)
Detectron: Facebook’s Object Detection

我收集了下面的论文

---

1. Scalable High Quality Object Detection ↩︎

2. Inception Network ↩︎

3. Single Shot MultiBox Detector ↩︎

4. FPN ↩︎ ↩︎

5. YOLOv3, stronger, better ↩︎

6. R-CNN ↩︎

7. Fast R-CNN ↩︎ ↩︎

8. Faster R-CNN ↩︎

9. R-FCN ↩︎

10. Mask RCNN ↩︎

11. Soft NMS ↩︎

12. Learning non-max-suppresion ↩︎ ↩︎ ↩︎

13. IoU-Net ↩︎

14. Softer NMS ↩︎

15. Relation Network ↩︎