【神经网络和深度学习-开发案例】 第一章 感知器和S型神经元
【神经网络和深度学习】
第一章 感知器-S型神经元
案例:使用神经网络识别手写数字
大多数人毫不费力地认出这些数字是504192。、
虽然这好像很容易,但是我们完全没有意识到这是一个非常复杂的过程。
在我们大脑的每一个半球,人类都有一个初级的视觉皮层,也被称为V1,包含1.4亿个神经元,它们之间有数百亿的连接。然而,人类的视觉不仅涉及到V1,还包括一系列的视觉皮质——V2、V3、V4和V5——正在进行越来越复杂的图像处理。我们的脑袋里装着一台超级计算机,经过数亿年的进化,我们的大脑已经被进化了,并且能够很好地适应视觉世界。识别手写数字并不容易。相反,我们人类是惊人的,非常善于理解我们的眼睛给我们看的东西。但几乎所有的工作都是无意识的。所以我们通常不会意识到我们的视觉系统解决了一个问题。
如果你试图编写一个计算机程序来识别上面的数字,那么视觉模式识别的难度就会变得明显。当我们自己做的时候,似乎很容易就会变得非常困难。关于我们如何识别形状的简单直观——“9在顶部有一个循环,在右下方有一个垂直的笔画”——事实证明,用算法来表达并不那么简单。当你试图精确地制定这些规则时,你很快就会迷失在异常、警告和特殊情况的泥沼中。看来无望。
神经网络以一种不同的方式处理这个问题。我们的想法是用大量的手写数字,也就是所谓的训练例子,
然后开发一个系统,可以从这些训练的例子中学习。换句话说,神经网络使用这些例子来自动推断出识别手写数字的规则。此外,通过增加培训案例的数量,网络可以更多地了解笔迹,从而提高其准确性。因此,虽然我在上面只展示了100个训练数字,也许我们可以用成千上万甚至上百万的训练例子来建立一个更好的手写识别器。
在这一章中,我们将编写一个计算机程序来实现一个神经网络,学习识别手写的数字。该程序只有74行长,并且不使用特殊的神经网络库。但是这个简短的程序可以在没有人工干预的情况下识别出超过96%的数字。此外,在后面的章节中,我们将开发出能够提高精确度的想法,超过99%。事实上,最好的商业神经网络现在已经很好了,它们被银行用来处理支票,并通过邮局来识别地址。
我们关注的是手写识别,因为它是一个很好的原型问题,用于学习神经网络。作为一个原型,它达到了一个最佳的位置:它是具有挑战性的——识别手写的数字是不小的壮举——但这并不难,需要一个极其复杂的解决方案,或者巨大的计算能力。此外,这是一种开发更高级技术的好方法,比如深度学习。因此,在整本书中,我们会反复提到手写识别的问题。在书的后面,我们将讨论这些想法如何应用于计算机视觉的其他问题,以及语言、自然语言处理和其他领域。
当然,如果这一章的目的仅仅是写一个计算机程序来识别手写的数字,那么这个章节就会短得多!但在此过程中,我们将开发许多关于神经网络的关键概念,包括两种重要的人工神经元(感知机和sigmoid神经元),以及神经网络的标准学习算法,即所谓的随机梯度下降法。自始至终,我都专注于解释为什么事情会按照他们的方式进行,以及建立你的神经网络直觉。这需要一个更长的讨论,而不是我刚刚展示了正在发生的事情的基本机制,但这是值得的,因为你将获得更深入的理解。在回报中,在这一章的结尾,我们将能够理解深度学习是什么,以及它为什么重要。
感知器
什么是神经网络?首先,我将解释一种叫做感知器的人工神经元。感知器是由科学家弗兰克罗森布拉特在20世纪50年代和60年代发明的,灵感来自于沃伦麦卡洛克和沃尔特皮茨的早期作品。今天,使用其他的人工神经元模型更常见——在这本书中,在许多现代的神经网络研究中,使用的主要神经元模型叫做sigmoid神经元。我们很快就会得到sigmoid神经元。但是为了理解为什么s型神经元是这样定义的,我们有必要花点时间来理解感知器。
那么感知器是如何工作的呢?一个感知器需要几个二进制输入x1,x2,…,然后产生一个二进制输出:
在这个例子中,感知器有三个输入,x1,x2,x3。一般来说,它可以有更多或更少的输入。
(Rosenblatt) 罗森布拉特提出了一个计算输出的简单规则:
他引入了权重w1,w2,…,用实数表示各自输入对输出的重要性。
神经元的输出值0或1,是由加权的和 ∑jwjxj ∑ j w j x j 是否小于或大于某个阈值(threshold)决定的。就像权重一样,阈值是一个实数,它是神经元的一个参数。
这就是感知器的工作原理!
这是基本的数学模型。你能想到的一种感知器是它是一个通过权衡证据来做出决定的装置。让我举个例子。这不是一个非常现实的例子,但它很容易理解,我们很快就会得到更现实的例子。假设周末即将来临,你想去看电影。你可以通过权衡三个因素来做出你的决定:
- 天气好吗?
- 你的女朋友想陪你吗?
- 门票贵不贵。
我们可以用相应的二元变量x1,x2和x3来表示这三个因子。例如,如果天气好的话,我们就会得到x1=1,如果天气不好,x1=0。类似地,如果你的女朋友想要去的话,x2=1,如果不是的话,x2=0。同样的,x3门票也是如此。
现在,假设你非常喜欢这个电影,即使你的女朋友对此不感兴趣,你也想去。但也许你最的讨厌坏天气,如果天气不好,你不可能去看电影。
你可以用感知器来模拟这种决策。
- 天气 权重 w1=6
- 女朋友 权重 w2=2
- 门票 权重 w3=2
天气对你很重要是决定因素,而女朋友和门票价格为次要因素。
如果三个因素都为1,它们乘以权重的总和就是 6 +2 +2 = 10。如果天气和门票因素为1,女朋友因素为0,总和就变为 6 + 0 + 2 = 8。如果天气为0,门票和女朋友因素为1,总和就变成 0+2+2=4。
最后,假设阈值为5,感知器就实现了所需的决策模型。通过改变权重和阈值,我们还可以得到不同的决策模型。
显然,感知器并不是人类决策的完整模型!但是这个例子说明了一个感知器如何能够衡量不同种类的证据来做出决定。一个复杂的感知机网络可以做出非常微妙的决定,这似乎是合理的。
在这个网络中,感知机的第一列——我们称之为感知机的第一层—通过权衡输入的证据,做出了三个非常简单的决定。那么第二层的感知器呢?每一个感知机都在做一个决定,权衡第一层决策的结果。通过这种方式,第二层的感知器可以比第一层的感知机更复杂、更抽象。更复杂的决策可以由第三层的感知器做出。通过这种方式,一个多层的感知机网络可以进行复杂的决策。
顺便说一下,当我定义感知器时,我说过感知器只有一个输出。在上面的网络中,感知机看起来有多个输出。事实上,它们仍然是单输出。多个输出箭头仅仅是表示感知器输出被用作其他几个感知器的输入的一种有用的方式。它比绘制一条单独的输出线要小得多。
设 w⋅x = ∑jwjxj ∑ j w j x j ,b=−threshold ,
这就是感知器的简化模型!
S型神经元
我们如何为神经网络设计这样的算法呢?假设我们有一个感知器网络我们想用它来学习解决一些问题。例如,对网络的输入可能是来自扫描的、手写的数字图像的原始像素数据。我们希望网络能够学习权重和偏差,这样网络的输出就能正确地对数字进行分类。要了解学习是如何工作的,假设我们在网络中对某些权重(或偏差)做了一个小小的改变。我们想要的是这个小的重量变化只会引起网络输出的一个小的相应的变化。我们马上就会看到,这个属性将使学习成为可能。从图表上看,这是我们想要的(很明显,这个网络太简单了,无法完成手写识别!)
如果一个权重(或偏差)的微小变化只会导致输出的微小变化,那么我们就可以利用这个事实来修改权重和偏差,以使我们的网络以我们想要的方式表现得更多。例如,假设网络错误地将一个图像分类为“8”,当它应该是“9”时。我们可以弄清楚如何在权重和偏差上做一个小的改变,这样网络就更接近于将图像分类为“9”。然后我们再重复一遍,不断地改变权重和偏差来产生更好的输出。网络将会学习。
问题是,当我们的网络包含感知器时,这并不是发生的事情。事实上,网络中任何单个感知器的重量或偏差的微小变化有时会导致感知器的输出完全翻转,比如从0到1。这样的翻转可能会导致其他网络的行为以一种非常复杂的方式完全改变。因此,虽然您的“9”现在可能被正确地分类,但是网络在所有其他图像上的行为可能会以某种难以控制的方式完全改变。这使得我们很难看到如何逐渐改变权重和偏差,从而使网络更接近预期的行为。也许有一些聪明的方法来解决这个问题。但是,我们如何才能让感知器网络学习,这并不是显而易见的。
我们可以通过引入一种叫做sigmoid神经元的新型人工神经元来克服这个问题。Sigmoid神经元与感知器相似,但经过修改,它们的重量和偏差的微小变化只会导致它们的输出发生微小的变化。这是一个至关重要的事实,它将允许一个乙状神经元网络学习。
好的,让我来描述一下s型神经元。我们将用我们描绘感知器的方式来描述s型神经元:
就像感知器一样,S型神经元有输入,x1,x2,x3。但是,这些输入不只是0或1,也可以取0到1之间的任何值。例如0.638,这是一个神经元的有效输入。就像感知器一样,S型神经元对每个输入都有权重,w1,w2,和总体偏差b。但输出不是0或1,相反,它是σ(w⋅x+b),σ也就是所谓的sigmoid函数,有时被称为逻辑函数,这个新的神经元叫做逻辑神经元。记住这个术语是很有用的,因为这些术语被许多使用神经网络的人使用。但是,我们将继续使用sigmoid术语。它的定义是:
更明确地说,一个S型神经元的输出OUTPUT包含输入x1 ,x2,权重w1, w2和偏差b。
乍一看,S型神经元与感知器有很大的不同。如果您还不熟悉sigmoid函数的代数形式,那么它可能看起来不透明和令人生畏。事实上,感知器和S型神经元之间有许多相似之处,而sigmoid函数的代数形式更像是一个数学工具,而不是真正的理解障碍。
为了理解与感知器模型的相似性,假设z=w⋅x+b是一个很大的正数,σ(z)≈1,就像感知机一样。假设z=w⋅x+b是非常大的负数,σ(z)≈0,S型神经元的也近似于感知器。只有当w⋅x+b的尺寸适中时,才会有很多偏离感知器模型的地方。
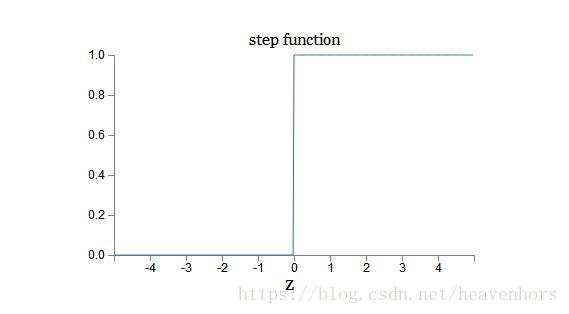
那么代数形式呢?我们怎么能理解呢?事实上,确切的形式并不重要——真正重要的是在绘制的时候函数的形状:
如果实际上是一个阶跃函数,那么S型神经元就会是一个感知器,因为输出是1或0,这取决于w x+b是正的还是负的,当w x+b=0时,感知器输出0,而阶跃函数输出1。
所以,严格地说,我们需要在那个点上修改阶跃函数。通过使用我们得到的实际函数,正如上面所暗示的,是一个平滑的感知器。所以函数的平滑度是关键的事实,而不是它的详细形式。在权重和b中,小的改变的平滑度将会产生一个小的变化输出,最后输出到神经元的输出。
虽然上面的表达式看起来很复杂,但是所有的偏导数,实际上是说一些非常简单的东西(这是一个非常好的消息):输出是 wj w j 和 b b 是权重和偏差上的一个线性函数。这种线性使得在权重和偏差中选择小的变化变得容易,从而实现输出的任何期望的小变化。因此,虽然S型神经元与感知机有许多相同的定性行为,但它们使我们更容易地发现,权重和偏差将如何改变输出。
我们应该如何解释一个S型神经元的输出?显然,感知器和S型神经元之间的一个大区别是,S型神经元不只是输出0或1。它们可以在0和1之间输出任何实数,所以0.173,0.689都是合法的输出。这可能是有用的,例如,如果我们想要使用输出值来表示图像输入中的像素的平均强度,以表示神经网络。但有时也会让人讨厌。假设我们想要来自网络的输出来表示“输入图像是9”或“输入图像不是9”。显然,如果输出是0或1,就像在感知器中一样,这是最容易做到的。但在实践中,我们可以建立一个约定来处理这个问题,例如,决定将至少0.505的输出解释为“9”,任何输出小于0.50.5表示“不是9”。
参考资料 http://neuralnetworksanddeeplearning.com/