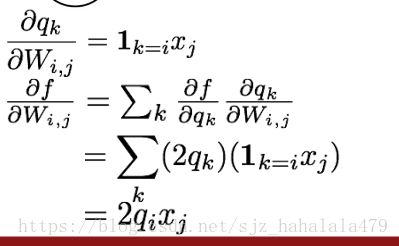斯坦福深度学习课程笔记(三)
介绍神经网络
官网
slides
1 反向传播
上节课介绍了两种方法去计算梯度,一种是数值法计算梯度,也就是根据导数的定义计算;另一种是分析法计算梯度,根据微积分,使用公式计算。
这节课介绍一种计算梯度的新方法,使用计算图的方式计算梯度。
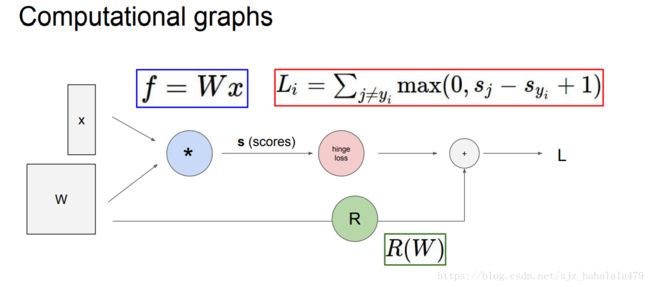
下图是svm多分类损失函数的一个计算图模型,计算图模型把公式中每个元素和符号都作为节点,连接起来。这个图模型有点类似于我们学编译原理的语法树,或者有限状态机,因为都是图模型嘛,差不了多少…
在图模型中,我们使用反向传播的方法计算梯度。下面是一个小例子:
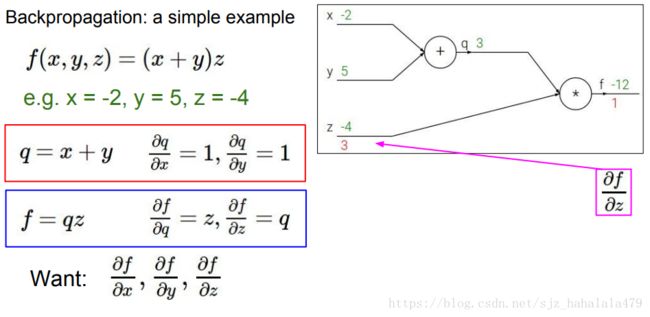
已知 f ( x , y , z ) = ( x + y ) z f(x,y,z) = (x+y)z f(x,y,z)=(x+y)z,求 ∂ f ∂ x \frac{\partial f}{\partial x} ∂x∂f, ∂ f ∂ y \frac{\partial f}{\partial y} ∂y∂f, ∂ f ∂ z \frac{\partial f}{\partial z} ∂z∂f的值。
如下图,为更好地说明,我们给 x , y , z x,y,z x,y,z赋上实值,然后沿着计算图正向传播先计算出中间值 q = x + y q=x+y q=x+y的值,再计算出最终值 f = q z f = qz f=qz的值。
之后,我们从最终值 f f f开始,反向计算梯度。 ∂ f ∂ f \frac{\partial f}{\partial f} ∂f∂f的值为1,所以乘法符号的上游梯度为1。
然后由于 f = q z f = qz f=qz, ∂ f ∂ q = z \frac{\partial f}{\partial q} = z ∂q∂f=z, ∂ f ∂ z = q \frac{\partial f}{\partial z} = q ∂z∂f=q,可以容易的计算出乘法节点下面 z z z分支的梯度为 q q q的值,即 3 3 3。乘法节点上面 q q q分支的梯度为 z z z的值,即 − 4 -4 −4。
继续反向传播到 x x x, y y y节点时,依据链式法则,节点最终的梯度值等于上游梯度值 upstream gradient与本地梯度值 local gradient相乘。

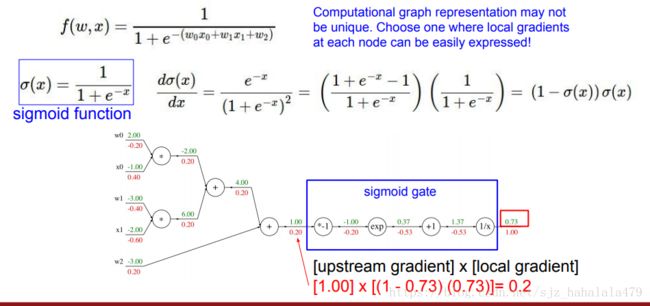
考虑另外一个更复杂的例子。首先正向传播算出所有中间值和最终值后,反向传播计算梯度。注意到 1 x \frac{1}{x} x1的导数是 − 1 x 2 - \frac{1}{x^2} −x21,应用链式法则,可以计算出倒数第二个节点的梯度。
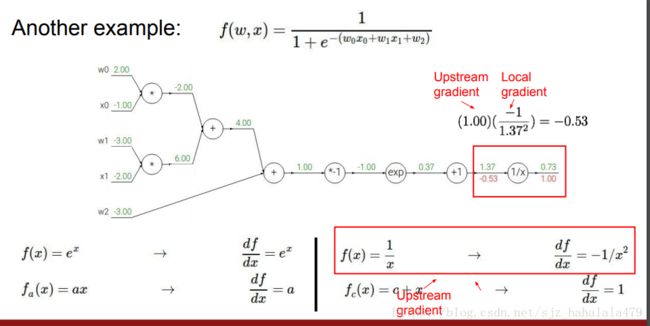
同一个公式的计算图并不是唯一的。上面的两个例子是把公式拆分到最细粒度,我们也可以将节点合并,如下图:蓝框框圈的地方可以合并为sigmoid函数。然后直接利用sigmoid的梯度公式求梯度值。
反向传播有三种很重要的模式:
- add gate: gradient distributor. 梯度分配器。也就是说加法门(节点)分支的梯度和上游梯度相等。
- max gate: gradient router.梯度路由。也就是说最大门(节点)某个分支(至值最大的那个分支)的梯度和上游节点相等,其它分支为0.
- mul gate: gradient switcher,梯度交换器。也就是说乘法门(节点)分支的梯度是另一个分支的值。
在深度学习中,变量一般是向量或矩阵的形式。那么,如何用反向传播法求向量变量的梯度呢?
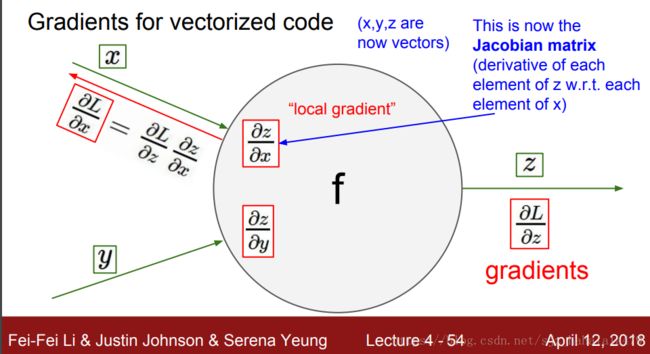
首先介绍一下雅各比矩阵(Jacobian Matrix):
以图中的 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z为例,假设 z z z是 m m m维向量, z = { z 1 , z 2 , . . . , z m } z = \{z_1,z_2,...,z_m\} z={z1,z2,...,zm}; x x x是 n n n维向量, x = { x 1 , x 2 , . . . x n } x = \{x_1,x_2,...x_n\} x={x1,x2,...xn},那么求 z z z对 x x x的偏导,可以使用雅各比矩阵:
J = [ ∂ z ∂ x 1 , ∂ z ∂ x 2 , ∂ z ∂ x 3 , . . . , ∂ z ∂ x n ] = ∣ ∂ z 1 ∂ x 1 ∂ z 1 ∂ x 2 ∂ z 1 ∂ x 3 . . . ∂ z 1 ∂ x n ∂ z 2 ∂ x 1 ∂ z 2 ∂ x 2 ∂ z 2 ∂ x 3 . . . ∂ z 2 ∂ x n . . . . . . . . . . . . . . . ∂ z m ∂ x 1 ∂ z m ∂ x 2 ∂ z m ∂ x 3 . . . ∂ z m ∂ x n ∣ ) J = [\frac{\partial z}{\partial x_1},\frac{\partial z}{\partial x_2},\frac{\partial z}{\partial x_3},...,\frac{\partial z}{\partial x_n}] = \begin{vmatrix} \frac{\partial z_1}{\partial x_1}&\frac{\partial z_1}{\partial x_2}&\frac{\partial z_1}{\partial x_3}&...&\frac{\partial z_1}{\partial x_n}\\ \frac{\partial z_2}{\partial x_1}&\frac{\partial z_2}{\partial x_2}&\frac{\partial z_2}{\partial x_3}&...&\frac{\partial z_2}{\partial x_n}&\\...&...&...&...&...\\\frac{\partial z_m}{\partial x_1}&\frac{\partial z_m}{\partial x_2}&\frac{\partial z_m}{\partial x_3}&...&\frac{\partial z_m}{\partial x_n}\end{vmatrix}) \\ J=[∂x1∂z,∂x2∂z,∂x3∂z,...,∂xn∂z]=∣∣∣∣∣∣∣∣∂x1∂z1∂x1∂z2...∂x1∂zm∂x2∂z1∂x2∂z2...∂x2∂zm∂x3∂z1∂x3∂z2...∂x3∂zm............∂xn∂z1∂xn∂z2...∂xn∂zm∣∣∣∣∣∣∣∣)
可以看到该雅各比矩阵有 m m m行 n n n列。
上图中的 f ( x ) f(x) f(x)是一个求 x x x和0的最大值的函数,输入 x x x有4096维,相应的 f ( x ) f(x) f(x)也有4096维,它们的雅各比矩阵如下:
J = ∣ ∂ m a x ( 0 , x 1 ) ∂ x 1 ∂ m a x ( 0 , x 1 ) ∂ x 2 . . . ∂ m a x ( 0 , x 1 ) ∂ x n ∂ m a x ( 0 , x 2 ) ∂ x 1 ∂ m a x ( 0 , x 2 ) ∂ x 2 . . . ∂ m a x ( 0 , x 2 ) ∂ x n . . . . . . . . . . . . ∂ m a x ( 0 , x n ) ∂ x 1 ∂ m a x ( 0 , x 1 ) ∂ x 2 . . . ∂ m a x ( 0 , x n ) ∂ x n ∣ ) J = \begin{vmatrix} \frac{\partial max(0,x_1)}{\partial x_1}&\frac{\partial max(0,x_1)}{\partial x_2}&...&\frac{\partial max(0,x_1)}{\partial x_n}\\ \frac{\partial max(0,x_2)}{\partial x_1}&\frac{\partial max(0,x_2)}{\partial x_2}&...&\frac{\partial max(0,x_2)}{\partial x_n}&\\...&...&...&...\\\frac{\partial max(0,x_n)}{\partial x_1}&\frac{\partial max(0,x_1)}{\partial x_2}&...&\frac{\partial max(0,x_n)}{\partial x_n}\end{vmatrix}) \\ J=∣∣∣∣∣∣∣∣∣∂x1∂max(0,x1)∂x1∂max(0,x2)...∂x1∂max(0,xn)∂x2∂max(0,x1)∂x2∂max(0,x2)...∂x2∂max(0,x1)............∂xn∂max(0,x1)∂xn∂max(0,x2)...∂xn∂max(0,xn)∣∣∣∣∣∣∣∣∣)
n = 4096 n=4096 n=4096,J为4096*4096的矩阵,而且可以明显看出该雅各比矩阵的性质是对角矩阵。
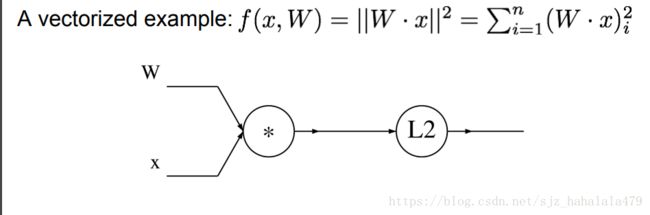
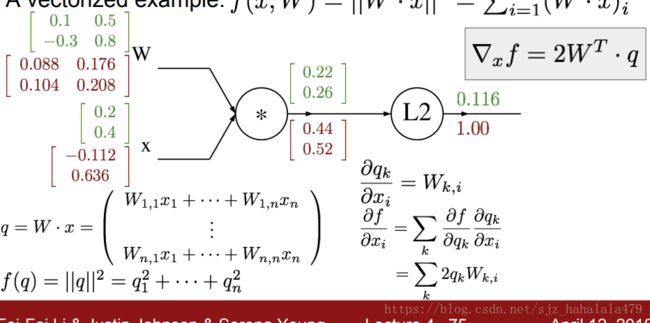
举一个计算图计算向量梯度的例子:
这个例子是计算f的L2范数。
在计算图中有两个gate,第一个门是乘法门,设中间值为 q q q,
q = W ⋅ x q = W \cdot x q=W⋅x
第二个门计算L2范数,
f = ∣ ∣ q ∣ ∣ 2 = q 1 2 + . . . + q n 2 f = ||q||^2 = q_1^2 + ...+q_n^2 f=∣∣q∣∣2=q12+...+qn2
令
W = ∣ 0.1 0.5 − 0.3 0.8 ∣ W =\begin{vmatrix} 0.1&0.5\\ -0.3&0.8\end{vmatrix} \\ W=∣∣∣∣0.1−0.30.50.8∣∣∣∣
x = ∣ 0.2 0.4 ∣ x =\begin{vmatrix} 0.2\\ 0.4\end{vmatrix} \\ x=∣∣∣∣0.20.4∣∣∣∣
所以
q = W ⋅ x = ∣ 0.1 0.5 − 0.3 0.8 ∣ ⋅ ∣ 0.2 0.4 ∣ = ∣ 0.1 ∗ 0.2 + 0.5 ∗ 0.4 − 0.3 ∗ 0.2 + 0.8 ∗ 0.4 ∣ = ∣ 0.22 0.26 ∣ q = W \cdot x = \begin{vmatrix} 0.1&0.5\\ -0.3&0.8\end{vmatrix} \cdot \begin{vmatrix} 0.2\\ 0.4\end{vmatrix} = \begin{vmatrix} 0.1*0.2+0.5*0.4\\ -0.3*0.2+0.8*0.4\end{vmatrix} = \begin{vmatrix} 0.22\\ 0.26\end{vmatrix} q=W⋅x=∣∣∣∣0.1−0.30.50.8∣∣∣∣⋅∣∣∣∣0.20.4∣∣∣∣=∣∣∣∣0.1∗0.2+0.5∗0.4−0.3∗0.2+0.8∗0.4∣∣∣∣=∣∣∣∣0.220.26∣∣∣∣
,
f = ∣ ∣ q ∣ ∣ 2 = 0.2 2 2 + 0.2 6 2 = 0.116 f = ||q||^2 = 0.22^2+0.26^2 = 0.116 f=∣∣q∣∣2=0.222+0.262=0.116
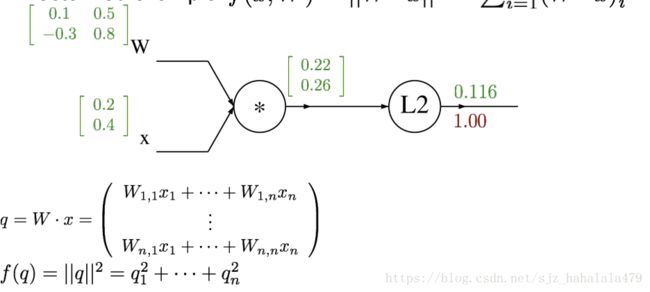
按计算图forward就是上图结果,然后反向计算梯度。
从1.0开始, L 2 L2 L2本地梯度是 2 q = ∣ 0.44 0.52 ∣ 2q = \begin{vmatrix} 0.44\\ 0.52\end{vmatrix} 2q=∣∣∣∣0.440.52∣∣∣∣,乘法的上游梯度就是 2 q ∗ 1 2q *1 2q∗1,也是刚刚的结果。
如何计算 ∂ q ∂ W \frac{\partial q}{\partial W} ∂W∂q,还有 ∂ q ∂ x \frac{\partial q}{\partial x} ∂x∂q呢?这需要用到雅各比矩阵。
分解开会发现如上规律,即
∇ w f = 2 q ⋅ x T \nabla_w f = 2q \cdot x^T ∇wf=2q⋅xT
同理,
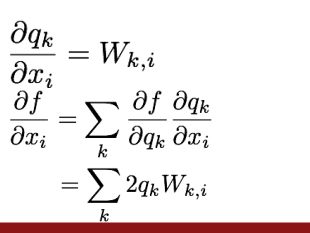
∇ x f = 2 W T ⋅ q \nabla_x f = 2W^T \cdot q ∇xf=2WT⋅q
在编写代码时,我们可以模块化编程,对于计算图,暴露出两个api。
class ComputationalGraph(object):
def forward(inputs):
pass
# 1. pass inputs to input gate
# 2. forward the computational graph
for gate in self.graph.nodes_topologically_sorted():
gate.forward()
return loss # the final gate in the graph outputs the loss
def backward():
for gate in reversed(self.graph.nodes_topologically_sorted()):
gate.backward()
return input_gradients
其中我们举一个gate对象的代码例子:
class MultiplyGate(object):
def forward(x,y):
z = x*y
self.x = x
self.y = y
return z
def backward(dz):
dx = self.y * dz
dy = self.x * dz
2 神经网络
神经网络就是一堆函数堆起来。比如说我们最开始,我们用的线性函数是
f 1 ( x ) = W 1 x f_1(x) = W_1x f1(x)=W1x
我们可以将 f 1 f_1 f1,再次作为自变量
f 2 ( x ) = W 2 m a x ( 0 , f 1 ( x ) ) f_2(x) = W_2max(0,f_1(x)) f2(x)=W2max(0,f1(x))
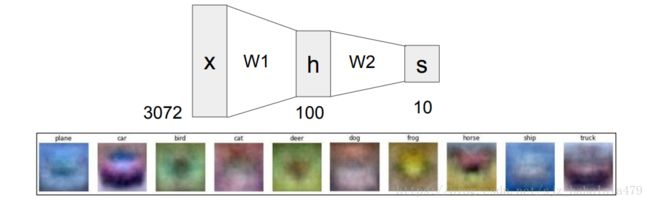
这样,就形成了一个两层的神经网络。其中,令
h = m a x ( 0 , f 1 ( x ) ) h = max(0,f_1(x)) h=max(0,f1(x))
h作为hidden layer,隐藏层存在,执行一个非线性的操作。
示意图如上。
将此神经网络与生物中的神经网络类比,实际上是十分不严谨的。但是它们还是有些相似之处。
比如,将输出传入神经元后,有一个激活函数;可以类比为生物中的放电率。
下面是一个20行的nn的例子
import numpy as np
from numpy.random import randn
N = 64
D_in = 1000
H = 100
D_out = 10
x = randn(N,D_in)
y = randn(N,D_out)
w1 = randn(D_in,H)
w2 = randn(H,D_out)
for t in range(2000):
#隐藏层的非线性函数h:sigmoid
h = 1 / (1 + np.exp(-x.dot(w1)))
y_pred = h.dot(w2)
loss = np.square(y_pred - y).sum()
print(t,loss)
grad_y_pred = 2 * (y_pred - y)
grad_w2 = h.T.dot(grad_y_pred)
grad_h = grad_y_pred.dot(w2.T)
grad_w1 = x.T.dot(grad_h * h * (1-h))
w1 -= 1e-4 * grad_w1
w2 -= 1e-4 * grad_w2
前50次输出如下:
0 43958.25687823094
1 25499.96015913513
2 17984.865430926475
3 14505.859434596383
4 12663.552460286908
5 11597.124443066588
6 10867.280233044621
7 10315.387745695552
8 9858.657235625595
9 9472.245476289512
10 9132.77967813943
11 8818.376198757163
12 8552.410276164566
13 8323.03494838262
14 8114.771796098317
15 7913.04617838718
16 7715.091753138132
17 7522.894286691011
18 7334.789907162314
19 7152.745292388772
20 6981.582454210624
21 6824.26503225578
22 6678.468849878009
23 6535.224388758432
24 6390.685408838475
25 6254.0954418228075
26 6129.235325704014
27 6014.260071562281
28 5905.375158219218
29 5799.139461394079
30 5691.935818565607
31 5578.4599987346555
32 5465.8980545904
33 5368.143218662671
34 5276.575886933
35 5188.527716428469
36 5103.078523022745
37 5019.580496488774
38 4937.14900774347
39 4854.523793114488
40 4770.966648061922
41 4688.5175426924425
42 4609.546947099343
43 4533.250456873415
44 4458.723567380121
45 4385.755612151515
46 4313.976463982253
47 4243.146539237559
48 4174.21123742844
49 4108.455207850091
50 4046.1295545954113
后50次输出如下:
1951 3.785884317856867
1952 3.778345544037649
1953 3.770823823217417
1954 3.7633191107754804
1955 3.7558313622262536
1956 3.748360533218758
1957 3.7409065795362646
1958 3.73346945709572
1959 3.726049121947405
1960 3.7186455302744013
1961 3.711258638392169
1962 3.7038884027481167
1963 3.6965347799211146
1964 3.6891977266211167
1965 3.6818771996886186
1966 3.674573156094308
1967 3.6672855529385844
1968 3.660014347451133
1969 3.6527594969904578
1970 3.645520959043503
1971 3.6382986912251494
1972 3.6310926512778563
1973 3.6239027970711546
1974 3.6167290866012918
1975 3.609571477990741
1976 3.602429929487834
1977 3.595304399466273
1978 3.5881948464247433
1979 3.581101228986504
1980 3.5740235058989134
1981 3.566961636033083
1982 3.5599155783833973
1983 3.5528852920671046
1984 3.5458707363239665
1985 3.538871870515722
1986 3.531888654125784
1987 3.524921046758791
1988 3.517969008140155
1989 3.511032498115714
1990 3.504111476651314
1991 3.497205903832322
1992 3.4903157398633393
1993 3.483440945067707
1994 3.476581479887162
1995 3.4697373048813644
1996 3.46290838072757
1997 3.4560946682201727
1998 3.4492961282703734
1999 3.442512721905671