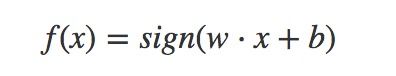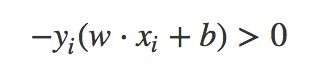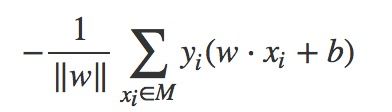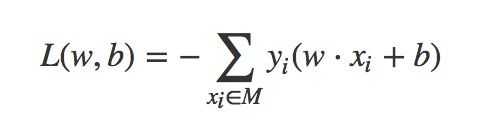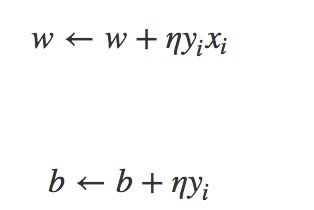《统计学习方法》-第二章感知机-学习总结

【感知机概述】

  感知机是一种二分类的线性分类模型，对于线性可分的数据集，什么叫做线性可分数据集？对于一个数据集，存在一个超平面能够将所有正负样本完全正确的划分在超平面的两侧，就称数据集为线性可分数据集。输入空间是样本的特征向量，输出空间是{-1,1},感知机旨在求出能够将训练数据进行线性划分的超平面。感知机的学习策略是最小化损失函数，利用随机梯度下降算法完成最小化损失函数，不断优化参数，最终的得到感知机模型。这是理解支持向量机的基础。

【感知机的模型】

由输入空间到输出空间的函数如下，为权值，b为偏置，sign是符号函数

模型的几何意义为，sign括号内的线性方程,对应于特征空间中的一个超平面，这里的x是一个多维向量，我们假设x是二维的向量，展开这个线性方程为,所以就相当于是这个平面和z=0这个平面的交线处，

画这个图的代码：

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
import numpy as np

fig = plt.figure(figsize=[20,9])
ax = fig.gca(projection='3d')
 
X = np.arange(-10, 10, 0.25)
Y = np.arange(-10, 10, 0.25)
X, Y = np.meshgrid(X, Y)
Z = 0.9*X +0.1* Y+1.0
Z2=0.0*X 
ax.plot_surface(X, Y, Z, cmap=cm.coolwarm,
                      linewidth=0, antialiased=False)
ax.plot_surface(X, Y, Z2, cmap=cm.coolwarm,
                      linewidth=0, antialiased=False)
ax.set_zlim(-10, 10)
ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))

看z=0这个平面上，画出上图的这条交线，

X = np.arange(-10, 10, 0.25)
Y=[-10.0+9.0*x for x in X]
plt.plot(X, Y)

 

这个（二维超平面）也就是直线，能够对即正样本和即负样本，进行线性的划分开来，下图打印出正负样本的z值，即将x1,x2代入的结果。

【感知机的策略】即确定损失函数

损失函数采用的是误分类点到超平面的总距离，首先空间中任意一点x0到超平面的距离公式如下，||W||是L2范数，即各元素的平方和再开方。

 由于对于错误分类的点，下式恒成立

因此误分类点到超平面的总距离可以替换为：

统计学习方法一书中不考虑1/||w||，从而损失函数变为

这个L(w,b)是一个非负的，如果没有错误分类点，则为0；错误分类点越少，离超平面总距离越小，损失函数也就越小。

【随机梯度下降优化参数】

对参数w和b，不断优化，先随机初始化，再随机取一个误分类点，通过更新参数的方式，调整w,b,使这个线性超平面向误分类点的一侧移动，减小误分类点与超平面的距离，再循环执行上面的过程，直至对所有点都正确分类。

感知机相当于是遇到一个误分类点就更新一下参数，不断使误分类点与划分平面的总距离变小，会因为参数初始化的不同，选取误分类点的顺序不同，而产生不同的线性分类模型，因此它的解不唯一，就如同下图，对于相同的训练集可能产生多个不同的感知机，那么你会如何选择呢？根据直觉我们会觉得第三条分类较好，那么至于原因，就引出了支持向量机。