神经网络中的激活函数(附Python代码实现)
激活函数分类
- 参考文档
- CS2131N: Commonly used activation
functions - 激活函数(ReLU, Swish,
Maxout)
- CS2131N: Commonly used activation
- 代码链接
- pyml by zhi
思维导图补充
恒等函数
- 函数表达式: y = x y = x y=x
- 函数特性: 线性
tanh
- tanh, sinh,
cosh - 函数表达式: y = t a n h ( x ) = e 2 x − 1 e 2 x + 1 y = {\rm tanh}(x) = {{e^{2x} - 1} \over {e^{2x} + 1}} y=tanh(x)=e2x+1e2x−1
- 函数特性: 非线性, 存在梯度弥散
Sigmoid
- sigmoid
- 函数表达式: y = e x e x + 1 y = {e^x \over {e^x + 1}} y=ex+1ex
- 函数特性: 非线性, 存在梯度弥散
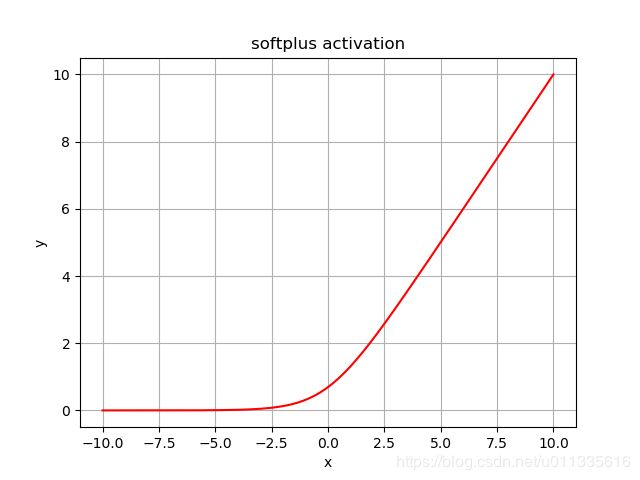
softplus
- 函数表达式: l o g ( e x + 1 ) {\rm log}(e^x + 1) log(ex+1)
- 函数特性: 非线性
softplus函数图像, 非线性函数.
softsign
- 函数表达式: x ( a b s ( x ) + 1 ) \frac{x} {({\rm abs}(x) + 1)} (abs(x)+1)x
- 函数特性: 非线性
elu
- 函数表达式: y = { x , x ≥ 0 e x − 1 , x < 0 y = \left\{ {\begin{array}{lll}{x,\;\;\;\;\;\;\;\;\;x \ge 0}\\{{e^x} - 1,\;\;\;x < 0}\end{array}}\right. y={x,x≥0ex−1,x<0
- 函数特性: 非线性
relu
- 函数表达式: m a x ( x , 0 ) {\rm max}(x, 0) max(x,0)
- 函数特性: 非线性+线性
relu6
- Convolutional Deep Belief Networks on CIFAR-10. A.
Krizhevsky - 函数表达式: m i n ( m a x ( x , 0 ) , 6 ) {\rm min}({\rm max}(x, 0), 6) min(max(x,0),6)
- 函数特性: 非线性+线性
leaky relu
- “Rectifier Nonlinearities Improve Neural Network Acoustic Models”
AL Maas, AY Hannun, AY Ng - Proc. ICML,
2013 - 函数表达式: y = { x , x ≥ 0 α x , x < 0 y = \left\{ {\begin{array}{lll}{x,\;\;\;\;\;\;x \ge 0}\\{\alpha x,\;\;\;x < 0}\end{array}} \right. y={x,x≥0αx,x<0
- 函数特性: 非线性+线性
selu
-
Self-Normalizing Neural Networks
-
函数表达式: y = λ { x , x ≥ 0 α ( e x − 1 ) , x < 0 y = \lambda \left\{ {\begin{array}{lll}{x,\;\;\;\;\;\;\;\;\;\;\;\;x \ge 0}\\{\alpha ({e^x} - 1),\;\;\;x < 0}\end{array}} \right. y=λ{x,x≥0α(ex−1),x<0
-
函数特性: 非线性, 自归一化
Swish
- Searching for Activation Functions" (Ramachandran et al.
2017) - 函数表达式:
y = x ⋅ s i g m o i d ( β x ) = e ( β x ) e ( β x ) + 1 ⋅ x y = x\cdot {\rm sigmoid}(\beta x) = {e^{(\beta x)} \over {e^{(\beta x)} + 1}} \cdot x y=x⋅sigmoid(βx)=e(βx)+1e(βx)⋅x - 函数特性: 非线性, 存在梯度弥散
实现代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Date : 2018-12-21 20:22:27
# @Author : Zhi Liu ([email protected])
# @Link : http://blog.csdn.net/enjoyyl
# @Version : $1.0$
import numpy as np
def linear(x):
r"""linear activation
:math:`y = x`
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
return x
def sigmoid(x):
r"""sigmoid function
.. math::
y = \frac{e^x}{e^x + 1}
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
ex = np.exp(x)
return ex / (ex + 1)
def tanh(x):
r"""Computes tanh of `x` element-wise.
Specifically
.. math::
y = {\rm tanh}(x) = {{e^{2x} - 1} \over {e^{2x} + 1}}.
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
# e2x = np.exp(2 * x)
# return (e2x - 1) / (e2x + 1)
return np.tanh(x)
def softplus(x):
r"""Computes softplus: `log(exp(x) + 1)`.
:math:`{\rm log}(e^x + 1)`
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
return np.log(np.exp(x) + 1)
def softsign(x):
r"""Computes softsign: `x / (abs(x) + 1)`.
:math:`\frac{x} {({\rm abs}(x) + 1)}`
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
return x / (np.abs(x) + 1)
def elu(x):
r"""Computes exponential linear element-wise. exp(x) - 1` if x < 0, `x` otherwise
.. math::
y = \left\{ {\begin{array}{*{20}{c}}{x,\;\;\;\;\;\;\;\;\;x \ge 0}\\{{e^x} - 1,\;\;\;x < 0}\end{array}} \right..
See `Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs) `_
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
return np.where(x < 0, np.exp(x) - 1, x)
def relu(x):
r"""Computes rectified linear: `max(x, 0)`.
:math:`{\rm max}(x, 0)`
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
# x[x < 0] = 0
# return x
return np.where(x > 0, x, 0)
def relu6(x):
r"""Computes Rectified Linear 6: `min(max(x, 0), 6)`.
:math:`{\rm min}({\rm max}(x, 0), 6)`
`Convolutional Deep Belief Networks on CIFAR-10. A. Krizhevsky `_
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
maxx = np.where(x > 0, x, 0)
return np.where(maxx < 6, maxx, 6)
def selu(x):
r"""Computes scaled exponential linear: `scale * alpha * (exp(x) - 1)` if < 0, `scale * x` otherwise.
.. math::
y = \lambda \left\{ {\begin{array}{*{20}{c}}{x,\;\;\;\;\;\;\;\;\;\;\;\;\;x \ge 0}\\{\alpha ({e^x} - 1),\;\;\;\;x < 0}\end{array}} \right.
where, :math:`\alpha = 1.6732632423543772848170429916717` , :math:`\lambda = 1.0507009873554804934193349852946`
See `Self-Normalizing Neural Networks `_
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
alpha = 1.6732632423543772848170429916717
scale = 1.0507009873554804934193349852946
return np.where(x < 0, scale * alpha * (np.exp(x) - 1), scale * x)
def crelu(x):
r"""Computes Concatenated ReLU.
Concatenates a ReLU which selects only the positive part of the activation
with a ReLU which selects only the *negative* part of the activation.
Note that as a result this non-linearity doubles the depth of the activations.
Source: `Understanding and Improving Convolutional Neural Networks via
Concatenated Rectified Linear Units. W. Shang, et
al. `_
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
return x
def leaky_relu(x, alpha=0.2):
r"""Compute the Leaky ReLU activation function.
:math:`y = \left\{ {\begin{array}{*{20}{c}}{x,\;\;\;\;\;\;x \ge 0}\\{\alpha x,\;\;\;x < 0}\end{array}} \right.`
`Rectifier Nonlinearities Improve Neural Network Acoustic Models `_
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
return np.where(x < 0, alpha * x, x)
def swish(x, beta=1.0):
r"""Computes the Swish activation function: `x * sigmoid(beta*x)`.
:math:`y = x\cdot {\rm sigmoid}(\beta x) = {e^{(\beta x)} \over {e^{(\beta x)} + 1}} \cdot x`
See `"Searching for Activation Functions" (Ramachandran et al. 2017) `_
Arguments:
x {lists or array} -- inputs
Returns:
array -- outputs
"""
ex = np.exp(beta * x)
return (ex / (ex + 1)) * x
if __name__ == '__main__':
import matplotlib.pyplot as plt
colors = ['k', 'm', 'b', 'g', 'c', 'r',
'-.m', '-.b', '-.g', '-.c', '-.r']
activations = ['linear', 'tanh', 'sigmoid', 'softplus', 'softsign',
'elu', 'relu', 'selu', 'relu6', 'leaky_relu', 'swish']
# 'elu', 'relu', 'selu', 'crelu', 'relu6', 'leaky_relu']
x = np.linspace(-10, 10, 200)
# for activation in activations:
# print("---show activation: " + activation + "---")
# y = globals()[activation](x)
# plt.figure()
# plt.plot(x, y, 'r')
# plt.title(activation + ' activation')
# plt.xlabel('x')
# plt.ylabel('y')
# plt.grid()
# plt.show()
plt.figure()
for activation, color in zip(activations, colors):
print("---show activation: " + activation + "---")
y = globals()[activation](x)
plt.plot(x, y, color)
plt.title('activation')
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.legend(activations)
plt.show()