深度学习系列(1):感知机
深度学习系列(1):感知机
前言
小论文总算告一段落了,近期开始深度学习了,跟着Hinton神经网络公开课边看边总结。视频参考链接如下:https://www.coursera.org/,搜索Neural Networks for Machine Learning即可找到资源。部分有中文翻译,当然也可以参考hankcs神犇关于Hinton神经网络的总结,参考链接如下:http://www.hankcs.com/ml/
思考
- 感知机是什么?
- 感知机如何实现?
- 感知机的优缺点?
感知机是什么?
大背景:给定输入,求得输出。中间需要一种模型来表达这种映射关系,于是有了: 输入 -> 模型(映射) -> 输出。
模型有很多,机器学习中有诸如SVM,DT,HMM等,这里我们只讨论神经网络的基础模型:感知机(perceptron)。
以下内容参考博文:
http://www.cnblogs.com/maybe2030/p/5597716.html#_label1
1943年,McCulloch和Pitts将上图的神经元结构用一种简单的模型进行了表示,构成了一种人工神经元模型,也就是我们现在经常用到的“M-P神经元模型”,如下图所示:
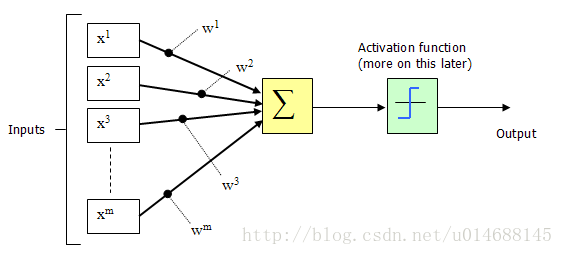
从上图M-P神经元模型可以看出,神经元的输出
其中 θ 为我们之前提到的神经元的激活阈值,函数 f(⋅) 也被称为是激活函数。如上图所示,函数 f(⋅) 可以用一个阶跃方程表示,大于阈值激活;否则则抑制。但是这样有点太粗暴,因为阶跃函数不光滑,不连续,不可导,因此我们更常用的方法是用sigmoid函数来表示函数函数 f(⋅) 。
定义:
感知机(perceptron)是由两层神经元组成的结构,输入层用于接受外界输入信号,输出层(也被称为是感知机的功能层)就是M-P神经元。下图表示了一个输入层具有三个神经元(分别表示为x0、x1、x2)的感知机结构:
根据上图不难理解,感知机模型可以由如下公式表示:
其中, w 为感知机输入层到输出层连接的权重,b表示输出层的偏置。事实上,感知机是一种判别式的线性分类模型,可以解决与、或、非这样的简单的线性可分(linearly separable)问题,线性可分问题的示意图见下图:
Okay,以上内容均属于感知机的定义部分,问题是如何根据给定的{输入集合}和{输出集合}得到{ w 的集合}?即如何学习?
感知机如何实现?
思路
根据限有参数 w (待求参数,未知)及给定的输入输出(已知)能够定义损失函数,以激活函数sigmoid为例:
其中满足:
我们的目标:需要求出给定集合 w∗ , L(w∗) 取得最小值。如果有解析解可以直接求导代入求出每个 w1,w2,⋯,wn , 然这里并没有解析解,所以我们采用一种迭代的手段,即【梯度下降】。
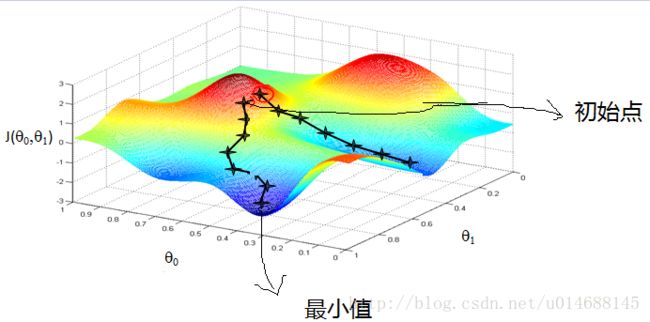
先看图,形象来说,由 w 构成的L在三维空间内是一种曲面图,梯度是在当前点,如红色初始点往四周看下降最快的方向。有了这个方向,我们乘以一个学习率 η ,就能让当前 w 朝着地势较低的方向前进了。
所以更新规则有:
而下降的方向实际上表示的一个值,数学上是 ∂L∂wi ,该值越大则地势越抖,走的也越快。所以在极值点时,导数为0,那么自然 wi 不在更新,算法收敛,求得最优。但正如图中所示,在非凸函数中,梯度下降无法保证求出的解一定是全局最优,这是它缺点之一,其次 η 学习率的选择也很重要,过大导致无法收敛,过小导致学习效率低,因此合理的,自适应的 η 也就成为了研究的热点。
所以数学上只要求出 ∂l∂wi ,就能写更新算法了。且收敛的条件可以用迭代次数或者参数 L(w) 的前后变化量控制。
感知机的弱点
问题1:
在Hinton神经网络公开课上,老爷子举了两个例子来说明感知机的弱点,第一个是关于XNOR的数据集:
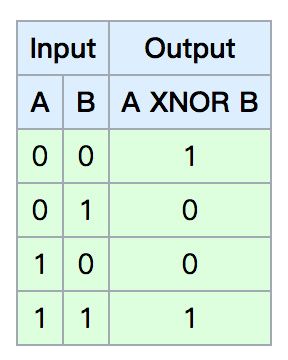
所以如果针对第一行有: w1+w2+0≥2θ ,针对第二行有: w1+w2<2θ ,需要找到这样的阈值使得上述两个不等式着实有点困难呐。
还有一份《证:单层感知机不能表示异或逻辑》,参考链接如下:http://blog.csdn.net/panda07100/article/details/38580993
问题 2:
n×1 的图片的模式识别,两种模式分别只有4个像素是黑色,其他都是白色,如下图:
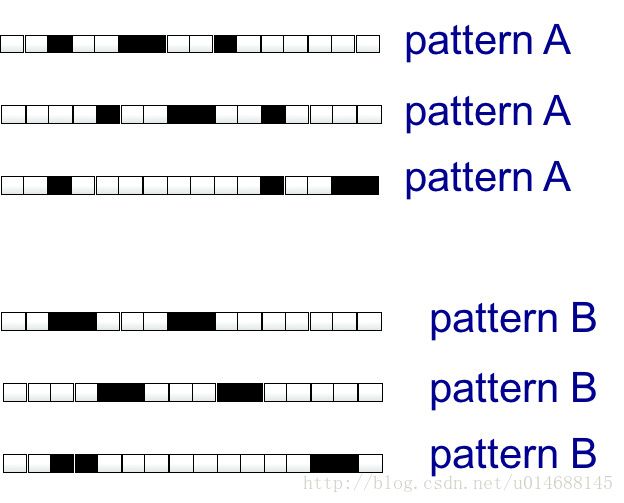
同样,对于这样的wrap-pattern数据集,感知机也无法区分模式A和模式B,歪?
此处需要考虑概率了,白色格子代表 xi=0 , 黑色格子代表 xj=1 ,所以对于 y=w1x1+w2x2+⋯+wnxn ,仅存在4个权值有效,于是有 y=wixi+wj+xj+wkxk+wlxl ,那么问题来了,推广到wrap,且大数据集上,每个格子都有被选中的机会,就上图而言被选中的概率为:4 / 16,所以每个格子都有25%的概率取黑色,于是有了 ∑y=416∑iwi ,这就呵呵了,模式B也是 ∑y=416∑iwi ,那么借用问题1的证明思路,阈值也出现了矛盾,即感知机无法区分上述两种简单的pattern。
总结:
参考老爷子和hankcs对视频的翻译:
但如果你手工选取有效的特征的话,感知机框架仍然有效。比如增加一些feature unit识别sub pattern。所以感知机模式识别的关键在于手写特征detector,而不是机器学习。老爷子说这个弱点被过分解读,导致早期很多人认为感知机不好用,那么神经网络也不好用。
如果有办法训练特征识别模块的话,神经网络就好用了。我们不但要学习特征权重,还要学习特征表示。第二代神经网络其实全是关于特征表示的学习(早期的神经网络没有hidden unit层,特征是原始的)。
多个线性的隐藏层无济于事,整个模型依然是线性的。于是怎么有效地训练非线性hidden unit就成为关键问题。学习流入hidden units的weight其实就是学习feature。