神经网络之感知器算法简单介绍和MATLAB简单实现

Perceptron Learning Algorithm

感知机学习算法，在1943年被生物学家MeCulloch和数学家Pitts提出以后，面临一个问题：参数需要依靠人工经验选定，十分麻烦。因此人们希望找到一种能够自己选定参数的方法。1957年，Frank Rosenblatt提出了Perceptron，是一种人工网络模型，并在这个基础上，提出了Perceptron学习算法，用于自动选定参数。




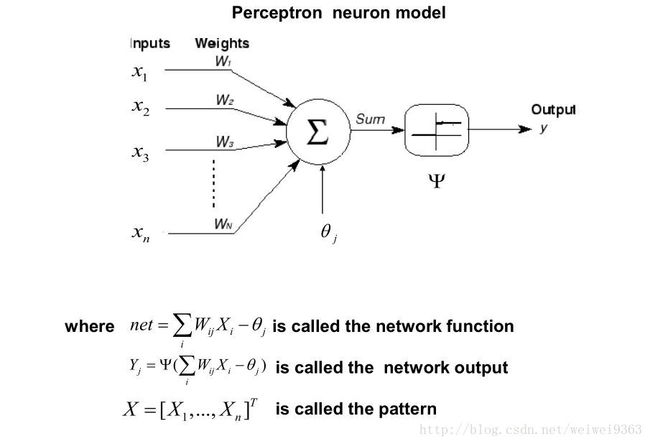
这里思考一个问题：为什么这个更新法则会成功收敛到正确的权值呢？在卡内基梅隆大学编写的《机器学习》中有提及这个问题。大致意思如下

为了得到直观的感觉，考虑一些特例。假定训练样本已经被感知器正确分类。这时， (Tj−Yj) 是0，这使得 ΔWij 为0，所以权值没有修改。而如果当目标输出是 +1 时，感知器输出一个 0 ，这种情况下为使感知器输出一个 +1 而不是 0 ，权值必须被修改以增大 WX 的值。例如，如果 Xi>0 ，那么增大 Wij 会使得感知器更接近正确分类的实例。注意，这种情况下训练法则会增长 Wij ，因为(T_j-Y_j)、 η 和 Xi 都是正。例如，如果 Xi=0.8 ， η=0.1 ， TJ=1 且 Yj=−1 ，那么权更新就是 ΔWij=η(Tj−Yj)=0.16 。另一方面，如果 Tj=−1 而 Yj=1 ，那么和正的 Xi 关联的权值会减小而不是增大。同理当 Xi<0 时，也有上面的收敛的性质。
事实上可以证明，在有限次地使用感知器训练法则后，上面的训练过程会收敛到一个能正确分类所有训练样例的权向量。前提是训练样例线性可分，并使用了一个充分小的 η （参加Minskey & Papert 19691）

需要注意的是，这个模型只能用于线性可分的数据，对于非线性可分的数据，上述的学习算法将无限循环。

MATLAB 实现

原理很简单，代码实现起来也不难。我们直接上代码
需要说明的是，我们的数据集，包括两个部分：数据和标签。Perceptron.m中的X，大致应该长这样:

X=[x1x2⋯L]

举个例子(逻辑运算OR)

X=⎡⎣⎢⎢⎢010100110111⎤⎦⎥⎥⎥

最后一列，只有0或者1，表示两类

Perceptron.m

function [ w, t ] = Perceptron( X, f, step, init_w, init_t )
%PRO Summary of this function goes here
%   X: data set with label
%   f: active function
%   step: step size
%   init_w:
%   init_t:
    if nargin < 5
       init_t = 0;
    end

    if nargin < 4
        init_w = [];
        init_t = 0;
    end

    if nargin < 3
        step = 0.1;
        init_w = [];
        init_t = 0;
    end


    label = X(:,end);
    data = X(:,1:end-1);

    [n_data,n_fea] = size(data);

    n_w = size(init_w);
    if n_w ~= n_fea
       init_w = ones(n_fea,1);
       n_w = n_fea;
    end
    w = init_w;
    t = init_t;
    while true
        result = f(data*w - t);
        result = label-result;
        index = find(result ~= 0);
        n_index = numel(index);
        if n_index == 0
            break
        end
        for i=1:n_index
           dis = result(index(i));
           for j=1:n_w
              w(j) = w(j) + step*dis*data(index(i),j);
           end
           t = t - step*dis;
        end
    end
end

demo.m 对Perceptron函数进行了简单的测试

clc;

c1 = [1 1];
c2 = [5 7];

n_L1 = 50; % number of item with label 1 
n_L2 = 20; % number of item with label 2

A = zeros(n_L1,3);
A(:,3) = 1;
B = zeros(n_L2,3);
B(:,3) = 0;

% create random point
for i=1:n_L1
    A(i,1:2) = c1 + rand(1,2);
end
for i=1:n_L2
    B(i,1:2) = c2 + rand(1,2);
end

%%
% show points
scatter(A(:,1), A(:,2),[],'r');
hold on
scatter(B(:,1), B(:,2),[],'g');

%%
% do perceptron
X = [A;B];
%X = [0 0 0;0 1 1;1 0 1;1 1 1];
[w, t] = Perceptron(X,@threshhold_func)

%%
% plot the result
A = w(1);
B = w(2);
C = -t;
if B==0
    %生成100个-C/A放在向量x中.
    x=linspace(-C/A,-C/A,100);
    %从-A)-(|A|+|B|+|C|)到|A|+|B|+|C|等距离生成100个值放在向量y中.?
    y=linspace(-abs(A)-abs(B)-abs(C),abs(A)+abs(B)+abs(C),100);
else
    %x从-A)-(|A|+|B|+|C|)到|A|+|B|+|C|,取步长为0.01.
    x=-abs(A)-abs(B)-abs(C):0.01:abs(A)+abs(B)+abs(C);
    y=(-A.*x-C)./B;
end
hold on
plot(x,y)

%%
% test
test_A = zeros(n_L1,3);
test_A(:,3) = 1;
test_B = zeros(n_L2,3);
test_B(:,3) = 0;
for i=1:n_L1
    test_A(i,1:2) = c1 + rand(1,2);
end
for i=1:n_L2
    test_B(i,1:2) = c2 + rand(1,2);
end
test_X = [test_A;test_B];
data = test_X(:,1:2);
label = test_X(:,end);
result = data*w - t;
index = find((label - result)~=0);
n_index = numel(index);
fprintf('正确率：%f\n', (n_index/(n_L1+n_L2)));

threshhold_func.m 阈值激活函数

function [ r ] = threshhold_func( x, t )
%UNTITLED Summary of this function goes here
%   Detailed explanation goes here
    if nargin < 2
        t = 0;
    end
    r = zeros(numel(x),1);
    index = find(x > t);
    r(index) = 1;
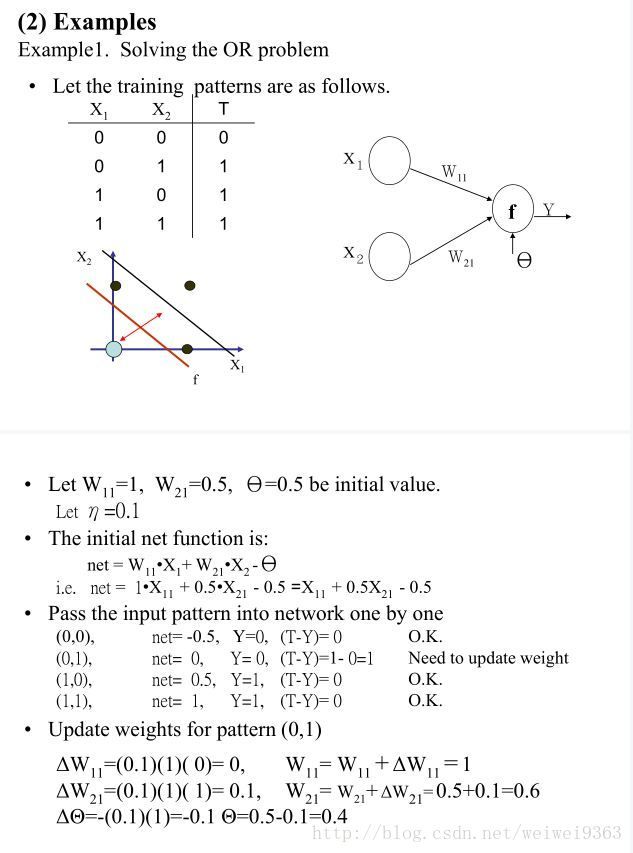
end

最后，给出老师课件上的例子，可以自己试试看计算过程是不是一致的。

---

1. Minsky M L, Papert S. Perceptrons : an introduction to computational geometry[M]// Perceptrons: An Introduction to Computational Geometry. The MIT Press, 1969:3356-62. ↩