算法设计与分析课程复习笔记11——单源最短路径
算法设计与分析课程复习笔记11——单源最短路径
单源最短路径
最短路径问题
输入:有权有向图G=(V,E)
路径p={ v 0 , v 1 , . . . , v k v_0, v_1, . . . , v_k v0,v1,...,vk}的权:
∑ i = 1 k w ( v i − 1 , v i ) \displaystyle \sum_{i=1}^kw(v_{i-1},v_i) i=1∑kw(vi−1,vi)
最短路径的权:
δ ( u , v ) = { m i n ( w ( p ) ) : u → v , i f t h e r e e x i s t a p a t h f r o m u t o v ∞ , o t h e r w i s e δ(u,v)=\left\{ \begin{aligned} min(w(p)):u → v, if there exist a path from u to v\\ \infty, otherwise\\ \end{aligned} \right. δ(u,v)={min(w(p)):u→v, if there exist a path from u to v∞, otherwise
最短路径的不同形式
- 单源最短路径
从给定的源顶点s到图中其他顶点v ∈ V的最短路径 - 单目的地最短路径
图中的顶点v ∈ V到某个给定的目的顶点t的最短路径
反向图,演变为单源最短路径问题 - 单点对最短路径问题
给定两顶点u和v ,求u到v的最短路径 - 全对点最短路径问题
图中所有点对之间的最短距离
最短路径的优化基础
给定G=(V,E)
权函数
v 1 v_1 v1到 v k v_k vk的最短路径p
p的部分路径 p i j p_{ij} pij
那么要求:p的部分路径 p i j p_{ij} pij也是最短路径
权值为负的边
负权边可能形成负权回路,如果从源顶点s能够抵达负权回路的顶点v,则有: w(s, v) = - ∞ \infty ∞
回路
最短路径可否有回路?不可以!!!
负权回路将导致:w(s, v) = - ∞ \infty ∞
正权回路显然不能加入,因为如有移除,将产生更短的路径
零权回路也不能加入,因为移除不会对最短路径的权产生任何影响
初始化算法
InitializeSingleSource(V,s)
for each v ∈ V
do d[v] ← ∞ \infty ∞
π[v] = NIL
d[s] ← 0
所有的最短路径算法都以初始化开始
缩短法
所谓对边(u, v)的缩短,即是检查能否通过顶点u,改善已有的到达v的最短路径
Relax(u,v,w)
if d[v] > d[u] + w(u,v)
then d[v] ← d[u] + w(u,v)
π[v] ← u
所有单源最短路径算法,从初始化算法开始,然后是缩短算法
算法之间的差别在于缩短算法的执行顺序和次数
Bellman-Ford算法
单源最短路径问题,允许负权值边,
返回值:如果从源顶点s没有可抵达的负权值回路,返回‘真’,其余的返回‘假’,无解
思想:遍历所有的边|V – 1|次,每次对每条边执行一次缩短运算
BellmanFord
InitializeSingleSource(V,s) Θ ( V ) Θ(V) Θ(V)
for i ← 1 to |V|-1 O ( V ) O(V) O(V)
do for each edge (u,v) ∈ E O ( E ) O(E) O(E)
do Relax(u,v,w)
for each edge (u,v) ∈ E O ( E ) O(E) O(E)
do if d[v] > d[u] + w(u,v)
then return FALSE
return TRUE
运行开销: O ( V E ) O(VE) O(VE)
最短路径特性
三角不等式
δ(s, v) ≤ δ(s, u) + w(u, v)
-上限特性
对于任何顶点v, d[v] ≥ δ(s, v)成立
一旦d[v] = δ(s, v)成立, d[v] 便不再改变
- 无通路特性
如果不存在从s到v的通路,则有d[v] = ∞ - 收敛性
如果s~u → v 是一条最短路径,在对边(u, v)进行缩短操作之前的任何时刻有d[u] = δ(s, u), 那么在对边(u, v)进行缩短操作之后的任何时刻有d[v] = δ(s, v) - 路径松弛特性
p = { v 0 , v 1 , . . . , v k v_0, v_1, . . . , v_k v0,v1,...,vk} 是从源顶点v 0 _0 0到 v k v_k vk的最短路径,如果缩短操作是按照( v 0 v_0 v0, v 1 v_1 v1), ( v 1 v_1 v1, v 2 v_2 v2), . . . , ( v k − 1 v_{k-1} vk−1, v k v_k vk)进行的,即使其中有其他缩短操作穿插,d[ v k v_k vk ] = δ(s, v k v_k vk)成立
DAG的单源最短路径
思想:
对图进行拓扑排序
依据拓扑排序对边进行缩短操作
DGA中没有负权值回路, 因此存在最短路径
DAG-SHORTEST-PATHS(G,w,s)
topologically sort the vertices of G(拓扑排序) Θ ( V + E ) Θ(V+E) Θ(V+E)
InitializeSingleSource(V,s)(初始化) Θ ( V ) Θ(V) Θ(V)
for each vertex u, taken in topologically sorted order(依据拓扑排序顶点顺序)
do for each vertex v ∈ Adj[u]
do Relax(u,v,w)
运行开销: Θ ( V + E ) Θ(V+E) Θ(V+E)
Dijkstra算法
- 单源最短路径,不存在负权值边界
- 两类顶点的集合,S:集合中顶点的最短路径已经确定,Q:V-S,极小优先队列,Q中的值是最短路径的估计
- 重复的从Q中选择具有最短估计距离的顶点进行处理
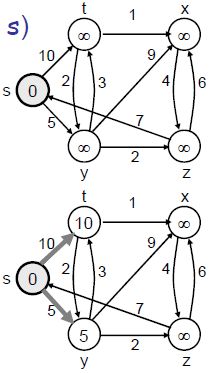
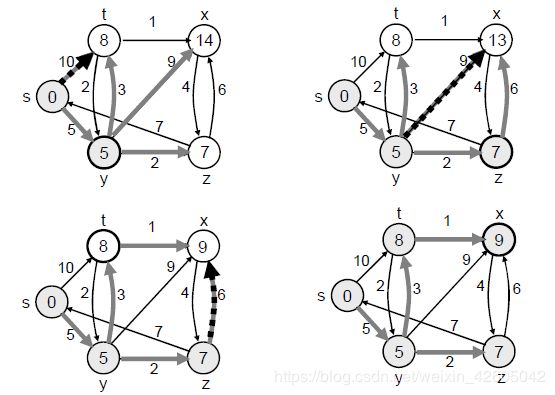
Dijikstra(G,w,s)
InitializeSingleSource(V,s)(初始化)
S ← 空集
Q ← V[G]
while Q ≠ 空集
u ← Extract-min(Q)
S ← S ∪ {u}
for each vertex v ∈ Adj[u]
do Relax(u,v,w)
参考:任课教师邱德红教授的课件