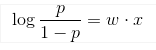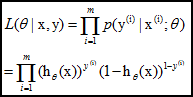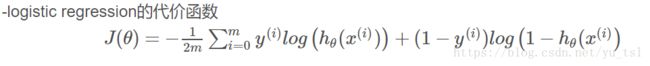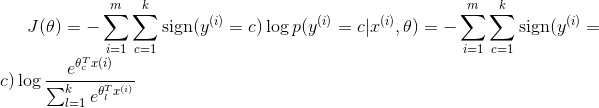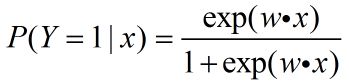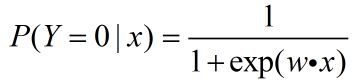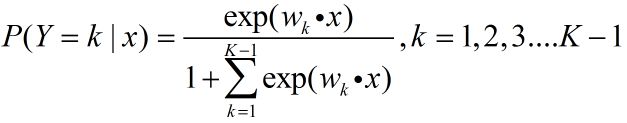机器学习算法之logistic regression
LR 算法特点:
优点:
计算代价不高,易于理解和实现;
预测结果是界于0和1之间的值。
缺点:
容易欠拟合,分类精度可能不高;
预测结果呈“S”型,概率变化很小,边际值太小,slope太小,而中间概率的变化很大,很敏感。 导致很多区间的变量变化对目标概率的影响没有区分度,不容易确定阀值。
公式推导:
模型解释:
1. 最大似然估计:
我们认为数据满足伯努利分布,即0-1分布,直觉上,一个线性模型的输出值 y 越大,这个事件 P(Y=1|x) 发生的概率就越大。 另一方面,我们可以用事件的几率(odds)来表示事件发生与不发生的比值,假设发生的概率是 p ,那么发生的几率(odds)是 p/(1-p) , odds 的值域是 0 到正无穷,几率越大,发生的可能性越大。将我们的直觉与几率联系起来的就是下面这个(log odds)或者是 logit 函数:
采用对数似然函数,对其求极大值,即可得到最终模型
带入公式即可得到对数几率,推荐一篇极大似然估计的文章:极大似然估计
2. 最小化损失函数:
3. 损失函数选择
通过极大似然估计得出
4. 多分类如何实现
有两种方式:
第一种方式
直接根据每个类别,都建立一个二分类器,带有这个类别的样本标记为1,带有其他类别的样本标记为0。假如我们有![]() 个类别,最后我们就得到了
个类别,最后我们就得到了![]() 个针对不同标记的普通的logistic分类器。
个针对不同标记的普通的logistic分类器。
第二种方式
修改logistic回归的损失函数,让其适应多分类问题。这个损失函数不再笼统地只考虑二分类非1就0的损失,而是具体考虑每个样本标记的损失。这种方法叫做softmax回归,即logistic回归的多分类版本。
我们首先简单介绍第一种方式。
对于二分类问题,我们只需要一个分类器即可,但是对于多分类问题,我们需要多个分类器才行。假如给定数据集![]() ,它们的标记
,它们的标记![]() ,即这些样本有
,即这些样本有![]() 个不同的类别。
个不同的类别。
我们挑选出标记为![]() 的样本,将挑选出来的带有标记
的样本,将挑选出来的带有标记![]() 的样本的标记置为1,将剩下的不带有标记
的样本的标记置为1,将剩下的不带有标记![]() 的样本的标记置为0。然后就用这些数据训练出一个分类器,我们得到
的样本的标记置为0。然后就用这些数据训练出一个分类器,我们得到![]() (表示针对标记
(表示针对标记![]() 的logistic分类函数)。
的logistic分类函数)。
按照上面的步骤,我们可以得到![]() 个不同的分类器。针对一个测试样本,我们需要找到这
个不同的分类器。针对一个测试样本,我们需要找到这![]() 个分类函数输出值最大的那一个,即为测试样本的标记:
个分类函数输出值最大的那一个,即为测试样本的标记:
![]()
下面我们介绍softmax回归。
对于有![]() 个标记的分类问题,分类函数是下面这样:
个标记的分类问题,分类函数是下面这样:
在这里,我们将上式的所有的![]() 组合起来,用矩阵
组合起来,用矩阵![]() 来表示,即:
来表示,即:
这时候,softmax回归算法的代价函数如下所示(其中![]() ):
):
很明显,上述公式是logistic回归损失函数的推广。
我们可以把logistic回归的损失函数改为如下形式:
但是,需要特别注意的是,对于![]() ,softmax回归和logistic回归的计算方式是不同的。
,softmax回归和logistic回归的计算方式是不同的。
对于选择softmax分类器还是![]() 个logistic分类器,取决于所有类别之间是否互斥。所有类别之间明显互斥用softmax分类器,所有类别之间不互斥有交叉的情况下最好用
个logistic分类器,取决于所有类别之间是否互斥。所有类别之间明显互斥用softmax分类器,所有类别之间不互斥有交叉的情况下最好用![]() 个logistic分类器。
个logistic分类器。
下面是多分类的讨论:
2.二分类器变多分类
具体来说,有以下三种策略:
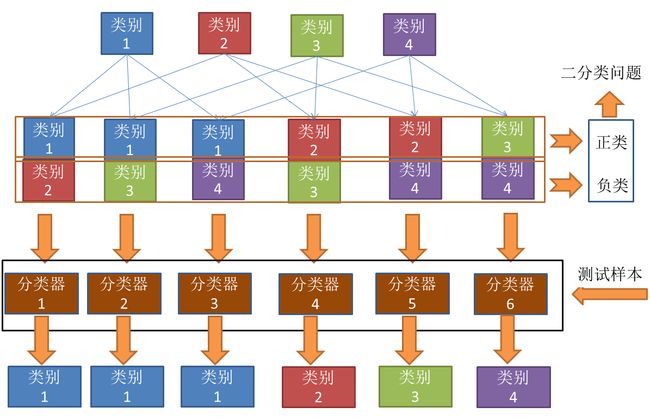
2.1 一对一 (OvO)
假如某个分类中有N个类别,我们将这N个类别进行两两配对(两两配对后转化为二分类问题)。那么我们可以得到 个二分类器。(简单解释一下,相当于在N个类别里面抽2个)
个二分类器。(简单解释一下,相当于在N个类别里面抽2个)
之后,在测试阶段,我们把新样本交给这 个二分类器。于是我们可以得到
个二分类器。于是我们可以得到 个分类结果。把预测的最多的类别作为预测的结果。
个分类结果。把预测的最多的类别作为预测的结果。
下面,我给一个具体的例子来理解一下。
上图的意思其实很明显,首先把类别两两组合(6种组合)。组合完之后,其中一个类别作为正类,另一个作为负类(这个正负只是相对而言,目的是转化为二分类)。然后对每个二分类器进行训练。可以得到6个二分类器。然后把测试样本在6个二分类器上面进行预测。从结果上可以看到,类别1被预测的最多,故测试样本属于类别1。
2.2 一对其余 (OvR)
一对其余其实更加好理解,每次将一个类别作为正类,其余类别作为负类。此时共有(N个分类器)。在测试的时候若仅有一个分类器预测为正类,则对应的类别标记为最终的分类结果。例如下面这个例子。
大概解释一下,就是有当有4个类别的时候,每次把其中一个类别作为正类别,其余作为负类别,共有4种组合,对于这4中组合进行分类器的训练,我们可以得到4个分类器。对于测试样本,放进4个分类器进行预测,仅有一个分类器预测为正类,于是取这个分类器的结果作为预测结果,分类器2预测的结果是类别2,于是这个样本便属于类别2。
其实,有人会有疑问,那么预测为负类的分类器就不用管了吗?是的,因为预测为负类的时候有多种可能,无法确定,只有预测为正类的时候才能唯一确定属于哪一类。比如对于分类器3,分类结果是负类,但是负类有类别1,类别2,类别4三种,到底属于哪一种?
2.3多对多(MvM)
所谓多对多其实就是把多个类别作为正类,多个类别作为负类。本文不介绍这个方法,详细可以参考周志华西瓜书P64-P65。
3.对于上面的方法其实都是训练多个二分类器,那么有没有更加直接的方法对LR来进行多分类呢?
我们知道,对于二分类的LR时,正类和负类的概率分别如下:
对于多分类,其实我只需要做简单的修改就可以了。
假设某分类任务有K个类别,那么对于每一个类别的概率有:
对于第K类来说
对于其余类而言
再利用极大似然估计即可。
说明:一个不错的解释 ,softmax 回归
二分类属于伯努利分布,多分类属于多项式分布
多分类问题
在一个多分类问题中,因变量y有k个取值,即。例如在邮件分类问题中,我们要把邮件分为垃圾邮件、个人邮件、工作邮件3类,目标值y是一个有3个取值的离散值。这是一个多分类问题,二分类模型在这里不太适用。
多分类问题符合多项分布。有许多算法可用于解决多分类问题,像决策树、朴素贝叶斯等。这篇文章主要讲解多分类算法中的Softmax回归(Softmax Regression)
推导思路为:首先证明多项分布属于指数分布族,这样就可以使用广义线性模型来拟合这个多项分布,由广义线性模型推导出的目标函数即为Softmax回归的分类模型。
仔细查看这篇文章,softmax 解释,就可以理解,多分类的实质。
二分类问题是多分类问题的一个特例,即是softmax的一种特例,但是值得注意的是softmax函数存在参数冗余问题,对于k类,采用k-1各参数即可。
进一步说,若成本函数 J(θ)J(θ) 被某组模型参数 (θ(1),θ(2),…,θ(k))(θ(1),θ(2),…,θ(k)) 最小化,那么对任意的 ψψ ,成本函数也可以被 (θ(1)−ψ,θ(2)−ψ,…,θ(k)−ψ)(θ(1)−ψ,θ(2)−ψ,…,θ(k)−ψ) 最小化。因此, J(θ)J(θ) 的最小值时的参数并不唯一。(有趣的是, J(θ)J(θ) 仍是凸的,并且在梯度下降中不会遇到局部最优的问题,但是 HessianHessian 矩阵是奇异或不可逆的,这将会导致在牛顿法的直接实现上遇到数值问题。)
注意到,通过设定 ψ=θ(K)ψ=θ(K) ,总是可以用 θ(K)−ψ=0⃗ (0⃗ 是全零向量,其元素值均为0)θ(K)−ψ=0→(0→是全零向量,其元素值均为0) 代替 θ(K)θ(K) ,而不会对假设函数有任何影响。因此,可以去掉参数向量 θθ 中的最后一个(或该向量中任意其它任意一个)元素 θ(K)θ(K) ,而不影响假设函数的表达能力。实际上,因参数冗余的特性,与其优化全部的 K⋅nK⋅n 个参数 (θ(1),θ(2),…,θ(K))(θ(1),θ(2),…,θ(K)) (其中 θ(k)∈Rnθ(k)∈ℜn),也可令 θ(K)=0⃗ θ(K)=0→ ,只优化剩余的 K⋅nK⋅n 个参数,算法依然能够正常工作。
逻辑回归常见问题总结 : https://www.cnblogs.com/ModifyRong/p/7739955.html