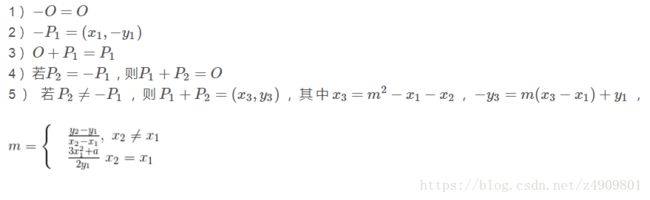区块链中的密码学技术——哈希算法、Merkle树、公钥密码算法

摘要： 本文是学习区块链技术中关于密码学这一部分的相关知识点学习总结整理。 哈希算法 Hash Function（哈希函数，也称散列函数） 定义 公式表示形式：  h=H(m)h=H(m) 函数说明： mm：任意长度消息（实际上有长度限制的，但因为长度可以非常大，这里可以认为是任意长度消息） HH：哈希函数 hh：固定长度的哈希值 典型的散列函数都有非常大的定义域，比如SHA-2最高接受(264−1)/8264−1)/8长度的字节字符串。

本文是学习区块链技术中关于密码学这一部分的相关知识点学习总结整理。

哈希算法

Hash Function（哈希函数，也称散列函数）

定义

公式表示形式： 

h=H(m)

函数说明： 
m：任意长度消息（实际上有长度限制的，但因为长度可以非常大，这里可以认为是任意长度消息） 
H：哈希函数 
h：固定长度的哈希值

 

典型的散列函数都有非常大的定义域，比如SHA-2最高接受(264−1)/8长度的字节字符串。同時散列函數一定有着有限的值域，比如固定长度的比特串（例如：256,512）。在某些情况下，散列函数可以设计成具有相同大小的定义域和值域间的單射。

1. 哈希函数定义——密码哈希函数是一类数学函数，可以在有限合理的时间内，将任意长度的消息压缩为固定长度的二进制串，其输出值称为哈希值，也称散列值。
2. 碰撞定义——是指两个不同的消息在同一哈希函数作用下，具有相同的哈希值。
3. 哈希函数的安全性——是指在现有的计算资源（包括时间、空间、资金等）下，找到一个碰撞是不可行的。
4. 抗弱碰撞性——对于给定的消息M1，要发现另一个消息M2，满足H(M1)=H(M2)在计算上是不可行的。
5. 抗强碰撞性——找任意一对不同的消息M1，M2，使H(M1)=H(M2)在计算上是不可行的。
6. 雪崩效应——当一个输入位发生变化时，输出位将有一半会发生变化。

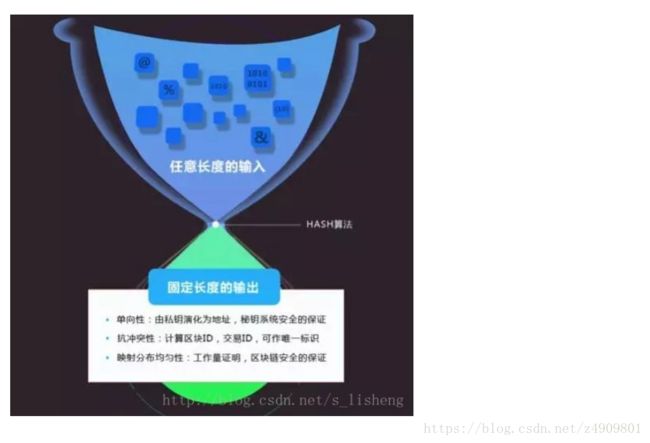
下图形象的说明了哈希函数：更多哈希函数的内容请参考：https://zh.wikipedia.org/wiki/%E6%95%A3%E5%88%97%E5%87%BD%E6%95%B8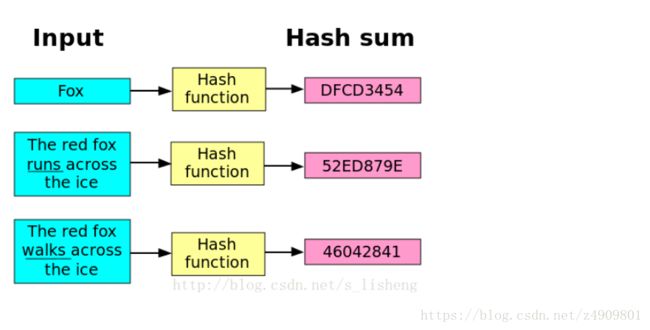 

哈希算法就是以哈希函数为基础构造的，常用于实现数据完整性和实体认证。

一个优秀的 hash 算法，将能实现：

• 正向快速：给定明文和 hash 算法，在有限时间和有限资源内能计算出 hash 值。
• 逆向困难：给定（若干） hash 值，在有限时间内很难（基本不可能）逆推出明文。
• 输入敏感：原始输入信息修改一点信息，产生的 hash 值看起来应该都有很大不同。
• 冲突避免：很难找到两段内容不同的明文，使得它们的 hash 值一致（发生冲突）。

在区块链中，常用两个密码学哈希函数，一个是SHA256，另一个是RIPEMD160（主要用于生产比特币地址）。

哈希函数的性质与应用

抗碰撞性

哈希函数的抗碰撞性是指寻找两个能够产生碰撞的消息在计算上是不可行的。但找到两个碰撞的消息在计算上不可行，并不意味着不存在两个碰撞的消息。哈希函数是把大空间上的消息压缩到小空间上，碰撞肯定存在。只是计算上是不可行的。例如，如果哈希值的长度固定为256位，显然如果顺序取1,2,⋯,2256+1这2256+1个输入值，计算它们的哈希值，肯定能够找到两个输入值，使得它们的哈希值相同。

原像不可逆

原像不可逆，指的是知道输入值，很容易通过哈希函数计算出哈希值；但知道哈希值，没有办法计算出原来的输入值。

难题友好性

难题友好性指的是没有便捷的方法去产生一满足特殊要求的哈希值。

一个哈希函数H称为难题友好的，如果对于每个n位的输出y，若k是从一个具有较高不可预测性（高小熵）分布中选取的，不可能以小于2n的时间找到一个x，使H(k||x)=y。

为了引申出工作量证明POW的原理，考虑一个由哈希函数构成的解谜问题：已知哈希函数H，一个高小熵分布的值value以及目标范围Y，寻找x，使得H(value||x)∈Y。

这个问题等价于需要找到一个输入值，使得输出值落在目标范围Y内，而Y往往是所有的输出值的一个子集。实际上，如果一个哈希函数H的输出位n位，那么输出值可以是任何一个0~2n范围内的值。预定义的目标范围Y的大小决定了这个问题的求解难度。如果Y包含所有n比特的串，那么问题就简单了，但如果Y只包含一个元素，那么这个求解是最难的，相当于给定一个哈希值，找出其中一个原像，原像不可逆的性质说明了这个难度。事实上，由于value具有高小熵分布，这确保了除了随机尝试x值以完成搜寻那个很大的空间外，没有其他有效的途径了。

哈希函数的难题友好性构成了基于工作量证明的共识算法的基础。通过哈希运算得出的符合特定要求的哈希值，可以作为共识算法中的工作量证明。这里比特币的安全保证依赖于哈希函数的安全性，如果哈希函数被攻破，可以想象POW共识算法就失效了，不用算力达到51%就可以攻击了。

补充数学概念——高小熵

小熵（min-entropy）是信息理论中衡量某个结果的可预测性的一个指标。

高小熵值的是变量呈均匀分布（随机分布）。如果我们从对分布的值进行随机抽样，不会经常抽到一个固定的值。例如，如果在一个128位的数中随机选一个固定的数n，那么选到该数的几率是1/2128。

SHA256

SHA256属于SHA（Secure Hash Algorithm，安全哈希算法）家族一员。详细可参考：https://zh.wikipedia.org/wiki/SHA%E5%AE%B6%E6%97%8F。是SHA-2算法簇中的一类。对于小于264位的消息，产生一个256位的消息摘要。

SHA-256其计算过程分为两个阶段：消息的预处理和主循环。在消息的预处理阶段，主要完成消息的填充和扩展填充，将所有输入的原始消息转换为n个512比特的消息块，之后对每个消息块利用SHA256压缩函数进行处理。

下面几节讲述的是如何计算Hash值，目前还没有完全理解，列在这里是为了有个宏观的概念，大致知道是什么回事，以后需要的时候再深入学习理解。

SHA256计算步骤：

step1： 附加填充比特。对报文进行填充使报文长度 n≡(448 mod 512)，填充比特数范围是1到512，填充比特串的最高位为1，其余位为0。（448=512-64，为了下面的64位）

step2 ： 附加长度值。将用64-bit表示初始报文（填充前）的位长度附加在step1的结果后（低字节位优先）。

step3： 初始化缓存。使用一个256bit的缓存来存放该哈希函数的中间值及最终结果。 
缓存表示为：A=0x6A09E667 , B=0xBB67AE85 , C=0x3C6EF372 , D=0xA54FF53A, 
E=0x510E527F , F=0x9B05688C , G=0x1F83D9AB , H=0x5BE0CD19

step4： 处理512bit（16个字）报文分组序列。该算法使用了六种基本逻辑函数，由64步迭代运算组成。每步都以256-bit缓存值ABCDEFGH为输入，然后更新缓存内容。每步使用一个32-bit 常数值Kt 和一个32-bit Wt。Kt是常数值，在伪代码中有它的常数值定义。Wt是分组之后的报文，512 bit=32bit*16，也就是Wt t=1,2..16由该组报文产生。Wt t=17,18,..,64由前面的Wt按递推公式计算出来。Wt递推公式在下面的伪代码有。 

step5 ：所有的512-bit分组处理完毕后，对于SHA-256算法最后一个分组产生的输出便是256-bit的报文摘要。 

SHA256计算流程

这里面公式太多，就直接截图了。 

伪代码实现

基本就是把上面的计算流程用伪代码翻译了一遍。（摘自：https://en.wikipedia.org/wiki/SHA-2）：

Note 1: All variables are 32 bit unsigned integers and addition is calculated modulo 2^32
Note 2: For each round, there is one round constant k[i] and one entry in the message schedule array w[i], 0 ≤ i ≤ 63
Note 3: The compression function uses 8 working variables, a through h
Note 4: Big-endian convention is used when expressing the constants in this pseudocode,
    and when parsing message block data from bytes to words, for example,
    the first word of the input message "abc" after padding is 0x61626380

Initialize hash values://初始向量
(first 32 bits of the fractional parts of the square roots of the first 8 primes 2..19):
h0 := 0x6a09e667
h1 := 0xbb67ae85
h2 := 0x3c6ef372
h3 := 0xa54ff53a
h4 := 0x510e527f
h5 := 0x9b05688c
h6 := 0x1f83d9ab
h7 := 0x5be0cd19

Initialize array of round constants:
(first 32 bits of the fractional parts of the cube roots of the first 64 primes 2..311):
k[0..63] :=
   0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
   0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
   0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
   0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
   0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
   0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
   0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
   0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2

Pre-processing://预处理阶段
begin with the original message of length L bits
append a single '1' bit
append K '0' bits, where K is the minimum number >= 0 such that L + 1 + K + 64 is a multiple of 512
append L as a 64-bit big-endian integer, making the total post-processed length a multiple of 512 bits

Process the message in successive 512-bit chunks:
break message into 512-bit chunks
for each chunk
    create a 64-entry message schedule array w[0..63] of 32-bit words
    (The initial values in w[0..63] don't matter, so many implementations zero them here)
    copy chunk into first 16 words w[0..15] of the message schedule array

    Extend the first 16 words into the remaining 48 words w[16..63] of the message schedule array:
    for i from 16 to 63
        s0 := (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor (w[i-15] rightshift 3)
        s1 := (w[i-2] rightrotate 17) xor (w[i-2] rightrotate 19) xor (w[i-2] rightshift 10)
        w[i] := w[i-16] + s0 + w[i-7] + s1

    Initialize working variables to current hash value:
    a := h0
    b := h1
    c := h2
    d := h3
    e := h4
    f := h5
    g := h6
    h := h7

    Compression function main loop://压缩函数主循环
    for i from 0 to 63
        S1 := (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25)
        ch := (e and f) xor ((not e) and g)
        temp1 := h + S1 + ch + k[i] + w[i]
        S0 := (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22)
        maj := (a and b) xor (a and c) xor (b and c)
        temp2 := S0 + maj

        h := g
        g := f
        f := e
        e := d + temp1
        d := c
        c := b
        b := a
        a := temp1 + temp2

    Add the compressed chunk to the current hash value:
    h0 := h0 + a
    h1 := h1 + b
    h2 := h2 + c
    h3 := h3 + d
    h4 := h4 + e
    h5 := h5 + f
    h6 := h6 + g
    h7 := h7 + h

Produce the final hash value (big-endian):
digest := hash := h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7

RIPEMD160

RIPEMD (RACE Integrity Primitives Evaluation Message Digest，RACE原始完整性校验讯息摘要)是一种加密哈希函数。RIPEMD-160是以原始版RIPEMD所改进的160位元版本，而且是RIPEMD系列中最常见的版本。

更多请参考：https://homes.esat.kuleuven.be/~bosselae/ripemd160.html

Merkle树

哈希指针链

哈希指针是一种数据结构，哈希指针指示某些信息存储在何处，我们将这个指针与这些信息的密码学哈希值存储在一起。哈希指针不仅是一种检索信息的方法，同时它也是一种检查信息是否被修改过的方法。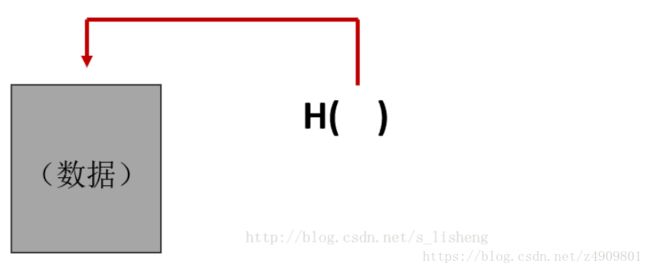 
 
上面的图表示了一个哈希指针，哈希指针是一个指向存储地点的指针，加上一个针对存储时信息的哈希值。

区块链就可以看作一类使用哈希指针的链表。这个链表链接一系列的区块，每个区块包含数据以及指向表中前一个区块的指针。区块链中，前一个区块指针由哈希指针所替换，因此每个区块不仅仅告诉前一个区块的位置，也提供一个哈希值去验证这个区块所包含的数据是否发生改变。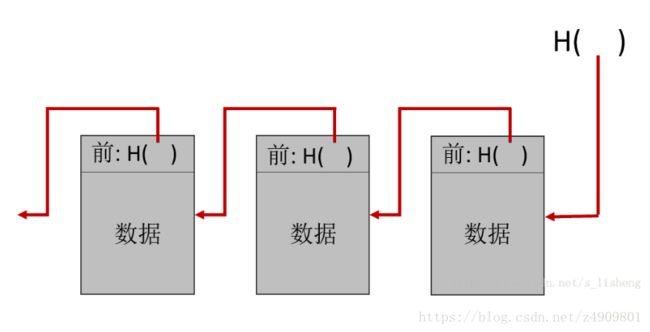 

Merkle哈希树

Merkle哈希树是一类基于哈希值的二叉树或多叉树，其叶子节点上的值通常为数据块的哈希值，而非叶子节点上的值，是将该节点的所有子节点的组合结果的哈希值。 

Merkle树一般用来进行完整性验证处理。在处理完整性验证的应用场景中，Merkle树会大大减少数据的传输量及计算的复杂度。

成员证明。如果想要证明一个确切的数据块是Merkle树中的一员。通常，只需要树根及这个区块和通向树根沿途的中间哈希值，就可以暂时忽略树的其他部分，这些就已经足以让我们验证到树根。 

区块链中的Merkle树是二叉树，如果在树上有n个节点，那么就只有log(n)个块需要被展示。因为每一个步骤都只需要计算下一级块的哈希，所以这大概只需要log(n)次去证明它。所以即使这个Merkle 树包含了非常多的块，我们依旧可以在一个较短的时间内证明一个成员块。

公钥密码算法

公钥密码体制(Public-key cryptography)

公钥密码体制的两个重要原则：

1. 第一，要求在加密算法和公钥都公开的前提下，其加密的密文必须是安全的。
2. 第二，要求所有加密的人和掌握私人密钥的解密人，他们的计算或处理都应比较简单，但对其他不掌握秘密密钥的人，破译应是极其困难的。

公钥密码算法简介

公钥密码算法中的密钥分为公钥和私钥，用户或系统产生一对密钥，将其中的一个公开，就是公钥，另一个自己保留，就是私钥。一般情况下，通信时，发送方利用公钥对信息进行加密，接收方利用私钥对信息进行解密完成通信。当然，也可用私钥加密，公钥解密。因为加密与解密用的是两个不同的密钥，所以这种算法也叫作非对称加密算法。

公钥密码系统的安全性都是基于难题的可计算问题。如：大数分解问题；计算有限域的离散对数问题；平方剩余问题；椭圆曲线的对数问题等。基于这些问题，就有了各种公钥密码体制。后面要讲的椭圆曲线密码算法是其中之一。

椭圆曲线密码算法

椭圆曲线密码算法（Elliptic Curve Cryptography,ECC）是基于椭圆曲线数学的一种公钥密码算法，其安全性依赖于椭圆曲线离散对数问题的困难性。

下面这3篇文章详细讲述了椭圆曲线密码算法的数学原理，不过是英文版的，但是讲述的非常详细，需要掌握的相关数学概念也讲述的很清楚。 
http://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/ 
http://andrea.corbellini.name/2015/05/23/elliptic-curve-cryptography-finite-fields-and-discrete-logarithms/ 
http://andrea.corbellini.name/2015/05/30/elliptic-curve-cryptography-ecdh-and-ecdsa/ 
下面这2篇是上面文章的翻译： 
http://blog.csdn.net/mrpre/article/details/72850598 
http://blog.csdn.net/mrpre/article/details/72850644 
这里理论不是很完善，具体的可深入学习Douglas R. Stinson的《密码学原理与实践》。

算法优点

1. 短的密钥长度，意味着小的带宽和存储要求。
2. 所有的用户可以选择同一基域上的不同的椭圆曲线，可使所有的用户使用同样的操作完成域运算。

椭圆曲线定义

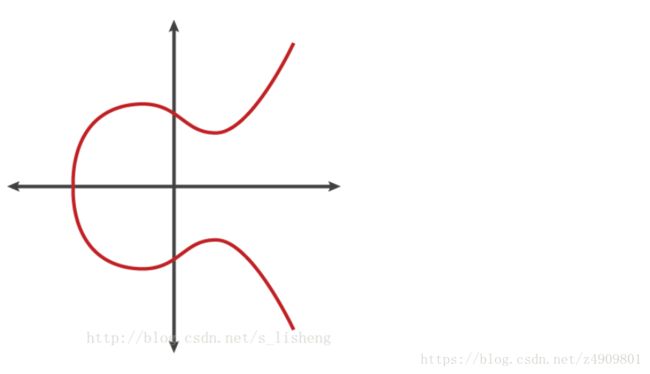
设p是一个大于3的素数，在有限域Fp上的椭圆曲线y2=x3+ax+b由一个基于同余式y2=x3+ax+b mod p的解集(x,y)∈Fp×Fp和一个无穷远点的特定点O组成，这里a,b∈Fp是满足4a3+27b2≠0 mod p的常数。

下图是显示了其中一种实际的椭圆曲线： 

对椭圆曲线上的点，我们可以定义一种形式的加法：如果椭圆曲线上的三个点位于同一直线上，那么它们的和为O（无穷远点）。 
根据上面的定义导出椭圆曲线上的加法运算法则如下： 
当P≠Q时： 

当P=Q时：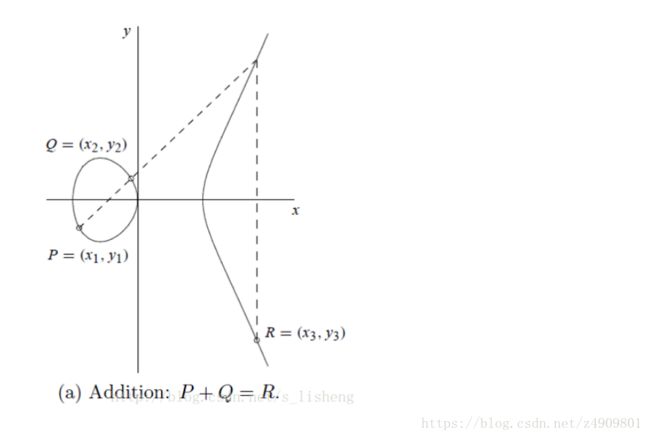 

下面的动画解释了为什么是切线： 
 
随着两个点越来越接近，过这两点的直线最终变成了曲线的切线

上面用几何的形式解释了椭圆曲线上的加法法则，下面是数学表达式。设P1=(x1,y1)与P2=(x2,y2)为椭圆曲线上的两个点，加减法运算如下： 

椭圆曲线上点群的离散对数问题

给定椭圆曲线上的点P和点Q，寻找数k，使得kP=Q，其中k称为Q的基于P的离散对数。 
在等式kP=P+P+⋯+P=Q中，已知k和点P，求点Q比较容易，反之已知点Q和点P，求k却是相当苦难的，这个问题称为椭圆曲线上点群的离散对数问题。椭圆曲线密码体制正是利用这个困难问题设计的。

在实际应用中，k作为私钥，而Q作为公钥。

这里补充一点，如何计算kP=P+P+⋯+P=Q

用这种形式表示时，计算kP似乎需要k次加法运算。如果k有n个二进制位，那么算法的时间复杂度将为O(2n)，这真不是很好。存在一些更快的算法。 
其中一种是“加倍（double)与相加（add)”算法。 
计算的原理可以用一个例子来更好地解释。取n=151。它的二进制表示形式为100101112 。这一二进制表示形式可以转换为一系列2的幂之和。

(取k的 每个二进制位上的数字，并用它乘以一个2的幂.) 
用这种方法，我们可以将k这样写:

secp256k1椭圆曲线

比特币系统的区块链实现中使用的椭圆曲线为secp256k1。所以这里需要学习一下。 
secp256k1曲线形如y2=x3+ax+b，由六元组D=(p,a,b,G,n,h)定义，其中： 
p=FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F=2256−232−29−28−27−26−24−1
a=0000000000000000000000000000000000000000000000000000000000000000 
b=0000000000000000000000000000000000000000000000000000000000000007 
The base point G in compressed form is（压缩形式表示的基点G定义）: 
G=0279BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
and in uncompressed form is（非压缩形式表示）: 
G=0479BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8
Finally the order n of G and the cofactor are（G的阶、协因子）:

G的阶：n=FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
协因子：h=01 
secp256k1椭圆曲线形状如下：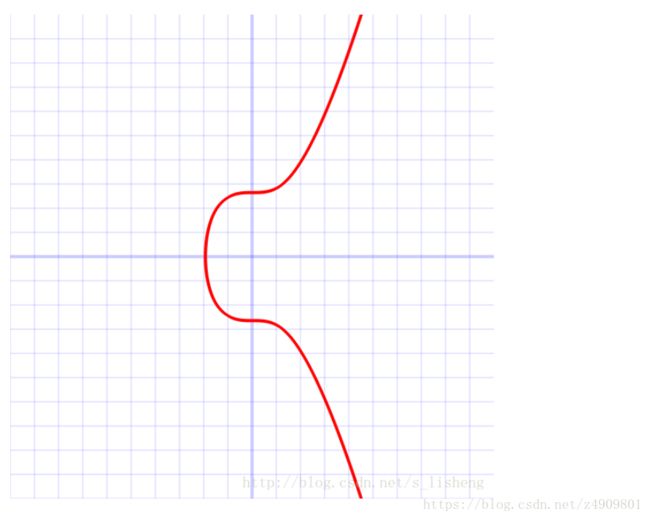 
 
This is a graph of secp256k1’s elliptic curve y2=x3+7 over the real numbers. Note that because secp256k1 is actually defined over the field Zp, its graph will in reality look like random scattered points, not anything like this. 
详细参考：https://en.bitcoin.it/wiki/Secp256k1

椭圆曲线参数 六元组解释： 
我们的椭圆曲线算法是工作在循环子群上的。几个参数含义如下： 
（1）素数p，这个值定义了有限域的大小 
（2）椭圆曲线的系数a、b 
（3）基点G（子群的生成元） 
（4）子群的阶n 
（5）协因子h (h=N/n)

椭圆曲线签名与验证签名

椭圆曲线数字签名生成

假设Alice希望对消息m进行签名，她所采用的椭圆曲线参数为D=(p,a,b,G,n,h)，对应的密钥对为(k,Q)，其中Q为公钥，k为私钥。Alice将按如下步骤进行签名。 
第1步，产生一个随机数d，1≤d≤n−1； （为什么是这个范围呢？在下面的”椭圆曲线的数乘和循环子群“及”子群的阶“中有讲述，这是个循环子群） 
第2步，计算dG=(x1,y1)，将x1转化为整数x1¯¯¯¯¯； 
第3步，计算r=x1¯¯¯¯¯ mod n，若r=0，则转向第1步； 
第4步，计算d−1 mod n； 
第5步，计算哈希值H(m)，并将得到的比特串转化为整数e； 
第6步，计算s=d−1(e+kr) mod n，若r=0，则转向第1步； 
第7步，(r,s)即为Alice对消息m的签名。

补充说明：d−1 is the multiplicative inverse of d modulo n.逆元。

椭圆曲线签名验证

为验证Alice对消息m的签名(r,s)，矿工可以得到Alice所用的椭圆曲线参数以及Alice的公钥Q。步骤如下： 
第1步，验证r和s是区间[1,n−1]上的整数； 
第2步，计算H(m)并将其转化为整数e； 
第3步，计算w=s−1 mod n； 
第4步，计算u1=ew mod n以及u2=rw mod n； 
第5步，计算X=u1G+u2G； 
第6步，若X=O，则拒绝签名，否则将X的x坐标x1转化为整数x1¯¯¯¯¯，并计算v=x1¯¯¯¯¯ mod n； 
第7步，当且仅当v=r时，签名通过验证。

为什么是这样计算，具体证明在这篇文章http://andrea.corbellini.name/2015/05/30/elliptic-curve-cryptography-ecdh-and-ecdsa/的这一节Correctness of the algorithm。以后需要深入的时候再看。

补充数学概念

同余式

数学上，同余（英语：congruence modulo，符号：≡）是数论中的一种等价关系。当两个整数除以同一个正整数，若得相同余数，则二整数同余。同余是抽象代数中的同余关系的原型。

两个整数a,b,若它们除以正整数m所得到的余数相等，则称a,b对于模m同余，记作a≡b (mod m)。读作a与b关于模m同余。（例 26≡14(mod 12)）。 
同余式的其他详细参考：https://zh.wikipedia.org/wiki/%E5%90%8C%E9%A4%98

密码学与有限循环群

现代密码学算法和协议中，消息是作为有限空间中的数字或元素来处理的。加密和解密的各种操作必须在消息之间进行变换，以使变换服从有限消息空间内部的封闭性。然而，数的一般运算诸如加减乘除并不满足有限空间内部的封闭性。所以密码算法通常运行于具有某些保持封闭性的代数结构的空间中，这种代数结构就是有限循环群。在数学中，群是一种代数结构，由一个集合以及一个二元运算组成。群必须满足以下四个条件：封闭性，结合律，存在单位元和存在逆元。 
最常见的群之一是整数集Z以及加法操作。 

有限循环群在群的基础上满足两个额外条件：群元素个数有限以及交换律。循环群由单个元素（产生元）的叠加操作生成，最常见的有限循环群为模拟时钟。 

椭圆曲线群定义

在数学上，椭圆曲线群的元素为椭圆曲线上的点，群操作为”+”,”+”的定义为，给定曲线两点P，Q，P+Q等于P和Q两点的连线与曲线交点沿X轴的对称点，如果P=Q，则P+P等于P在曲线上的切线与曲线交点沿X轴的对称点。该群的单位元为无穷远零点记作O=(0,0)，有P+O=P，点P的逆元为其沿X轴的对称点，记作−P。

椭圆曲线有限循环群

前面介绍的椭圆曲线都是基于有理数的，但是计算机运算浮点数(小数)的速度较慢，更重要的是四舍五入浮点数会产生误差，导致多次加密解密操作后原始消息不能被还原。故考虑到加密算法的可实现性，密码学上使用基于整数的模加运算产生椭圆曲线有限循环群。 
基于整数的模加运算的特点：

• 运算速度快
• 精确的运算结果
• 产生有限循环

下面举例说明，如何产生ECC有限循环群： 
例如考虑y2=x3−7x+10(mod 19)的集合，该集合中所有的元素如下图所示。模运算把发散的椭圆曲线映射到19*19的正方形空间中，并且保持了原有曲线的上下对称特性。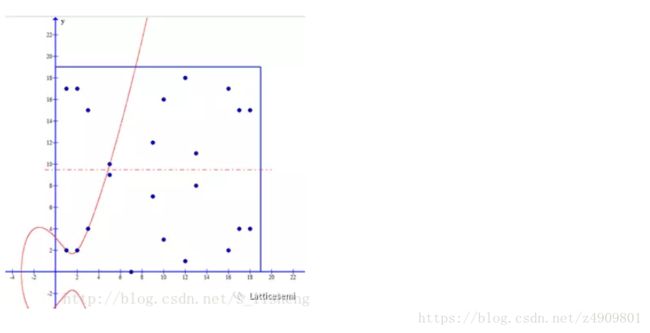 
 
下图展示了y2=x3−7x+10(mod 19)集合中的元素和椭圆曲线的关系。 
点Q′映射到点Q，点P的对称点也由点−P′映射到点−P。 
 
如果取一个更大的质数p进行模运算，集合中的元素点也会相应地增多。下图展示了利用同一个曲线方程进行不同模运算的结果。在实际的椭圆曲线加密算法中，使用长度为192-256位的质数p进行模运算。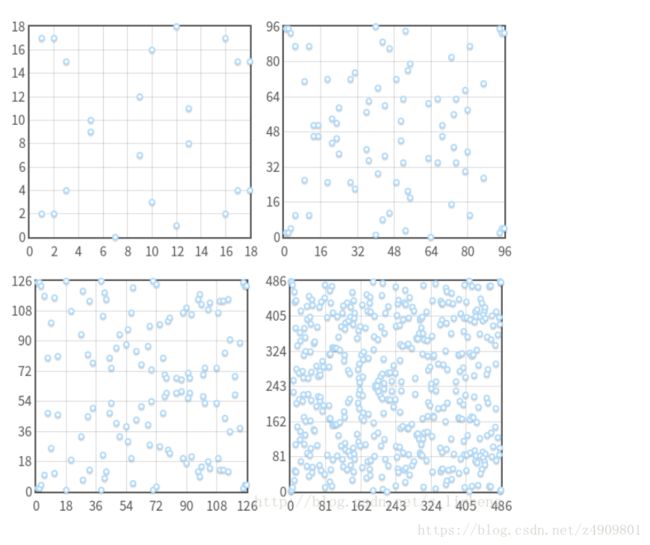 

现在我们基于y2=x3−7x+10(mod 19)，利用产生元P=(2,2)来生成ECC有限循环群。如下图所示。 
 

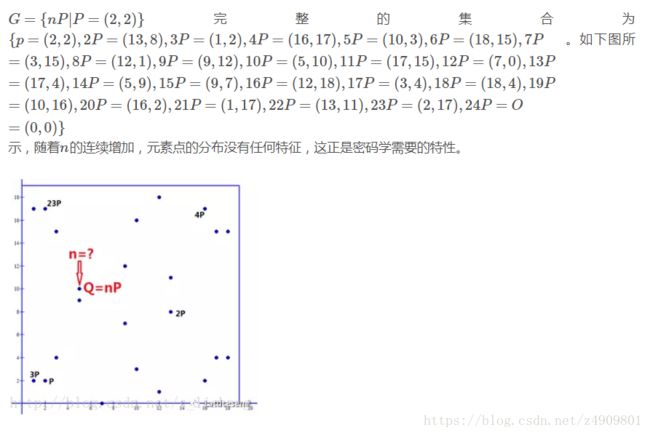
可参考：http://mp.weixin.qq.com/s/jOcVk7olBDgBgoy56m5cxQ

椭圆曲线的阶

椭圆曲线定义在有限域上，这也意味着，椭圆曲线上的点也是有限的。所以引出了一个问题：一个椭圆曲线到底有多少个点？

定义“椭圆曲线上点的个数”为 椭圆曲线的 阶 (order)。

至于怎么计算阶参考这篇文章吧： https://en.wikipedia.org/wiki/Schoof%27s_algorithm

椭圆曲线的数乘和循环子群

在实数域，数乘（标量乘法）被定义如下： 
 

上图可以化为下图的表示形式： 
 
结果显示点P的倍数的结果只有出现5个点，其他的点从未出现；其次他们是周期出现的。 显然，上面的5个点的集合，运算是封闭的。 
当然，不仅仅P有这样的性质，其他点也有类似的性质。 
即，P的加法构成了一个群S，由于S属于G，故S是G的子群。 
循环子群是ECC的基础。

子群的阶

1. 首先，我们已经定义了阶就是群中点的个数。在子群中也是这样的，但是我们可以换一种表达方式：子群的阶是最小能够使得nP=0的n。
2. 子群的阶和群的阶是有关系的。拉格朗日定理说明了，子群的阶是群的阶的因子。即如果N是群的阶，则其子群的阶n，则n是N的因子（n is a diviser of N）。

找到子群的阶的方法（根据上面讲述的定义和性质就能得出下面的方法）： 
（1）计算群的阶N 
（2）找出所有N的因子 
（3）每个N的因子n，然后乘以P 
（4）在3中，找出最小的n，使得满足nP=0。则n是子群的阶。

如何找一个基点

在ECC算法种，我们希望找到一个阶数较大的子群。 
通常我们会选择一个椭圆曲线，然后计算它的阶N，选择一个较大的因子n，然后找一个合适的基点。也就是说，我们不是首先找一个基点，然后计算它的阶，而是相反，我们先找到一个合适的阶，然后找以这个数为阶的子群的生成元。

首先，拉格朗日揭示，h=N/n是一个整数（当然，n是N的因子），h有一个自己的名字：cofactor of the subgroup（协因子）。

其次，每个椭圆曲线上的点P，NP=0，因为N是P的阶n的倍数。 
我们可以写成这样 n(hP)=0。 
假设n是一个素数，我们令G=hP，则G就是子群的生成元。 
n必须是素数，若非如此，则nP=0不一定表示n是P的阶，因为P的阶可能是n的一个因子。 
总结如下： 
1. 计算椭圆曲线的阶N。 
2. 选择一个数n当成子群的阶。n应该是N的素因数 
3. 计算h=N/n 
4. 随机选择一个点P 
5. 计算G=hP 
6. 如果G是0，到第4步。否则，我们找到了这个基点。