AI实战:推荐系统之矩阵分解算法(Matrix Factorization)
前言
前面2篇‘推荐系统之影视领域用户画像’的文章:
AI实战:推荐系统之影视领域用户画像——数据采集内容
AI实战:推荐系统之影视领域用户画像——标签数据清洗
本文介绍推荐系统中常见的方法:矩阵分解 Matrix Factorization,
Matrix Factorization分为python实现和tensorflow实现。
实战
-
一、用户行为数据
矩阵分解 (Matrix Factorization)用到的用户行为数据分为两种:第一种:显式数据。
是指用户对item的显式打分,比如用户对电影的评分。第二种:隐式数据。
是指用户对item的浏览、点击、购买、收藏、点赞、评论、分享等数据,其特点是用户没有显式地给item打分,用户对item的感兴趣程度都体现在他对item的上述行为的强度上。
本文介绍基于显示数据的矩阵分解(Matrix Factorization)。
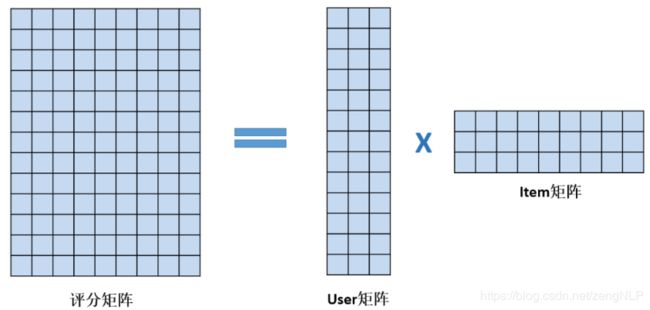
矩阵分解算法的输入是评分矩阵,输出是User矩阵和Item矩阵,如下图:
-
二、python实现MF
源码:
def matrix_factorization(M, K, n_steps=10000, alpha=0.0001, beta=0.001): # non negative regulaized matrix factorization implemention # M:评分矩阵 # K:隐藏层维度 # n_steps : the maximum number of n_steps to perform the optimisation, hardcoding the values # alpha : the learning rate, hardcoding the values # beta : the regularization parameter, hardcoding the values N = M.shape[0] #user数量 M = M.shape[1] #item数量 P = np.random.rand(N, K) Q = np.random.rand(M, K) Q = Q.T for step in xrange(n_steps): for i in xrange(M.shape[0]): for j in xrange(M.shape[1]): if M[i][j] > 0 : #calculate the error of the element eij = M[i][j] - np.dot(P[i,:],Q[:,j]) #second norm of P and Q for regularilization sum_of_norms = 0 #added regularized term to the error sum_of_norms += LA.norm(P) + LA.norm(Q) eij += ((beta/2) * sum_of_norms) #compute the gradient from the error for k in xrange(K): P[i][k] = P[i][k] + alpha * ( 2 * eij * Q[k][j] - (beta * P[i][k])) Q[k][j] = Q[k][j] + alpha * (2 * eij * P[i][k] - (beta * Q[k][j])) #compute total error error = 0 for i in xrange(M.shape[0]): for j in xrange(M.shape[1]): if M[i][j] > 0: error += np.power(M[i][j] - np.dot(P[i,:],Q[:,j]),2) if error < 0.001: break return P, Q.T -
三、TensorFlow实现MF
源码:
import tensorflow as tf import numpy as np class MF: def __init__(self, sess, M, k, learning_rate=0.0001, batch_size=256, reg_lambda=0.01): self.sess = sess self.n, self.m = M.shape self.k = k self.learning_rate = learning_rate self.batch_size = batch_size self.reg_lambda = tf.constant(reg_lambda, dtype=tf.float32) self.build_graph() def build_graph(self): self.u_idx = tf.placeholder(tf.int32, [None]) self.v_idx = tf.placeholder(tf.int32, [None]) self.r = tf.placeholder(tf.float32, [None]) self.U = self.weight_variable([self.n, self.k], 'U') self.V = self.weight_variable([self.m, self.k], 'V') self.U_bias = self.weight_variable([self.n], 'U_bias') self.V_bias = self.weight_variable([self.m], 'V_bias') self.U_embed = tf.nn.embedding_lookup(self.U, self.u_idx) self.V_embed = tf.nn.embedding_lookup(self.V, self.v_idx) self.U_bias_embed = tf.nn.embedding_lookup(self.U_bias, self.u_idx) self.V_bias_embed = tf.nn.embedding_lookup(self.V_bias, self.v_idx) self.r_hat = tf.reduce_sum(tf.multiply(self.U_embed, self.V_embed), reduction_indices=1) self.r_hat = tf.add(self.r_hat, self.U_bias_embed) self.r_hat = tf.add(self.r_hat, self.V_bias_embed) self.RMSE = tf.sqrt(tf.losses.mean_squared_error(self.r, self.r_hat)) self.l2_loss = tf.nn.l2_loss(tf.subtract(self.r, self.r_hat)) self.MAE = tf.reduce_mean(tf.abs(tf.subtract(self.r, self.r_hat))) self.reg = tf.add(tf.multiply(self.reg_lambda, tf.nn.l2_loss(self.U)), tf.multiply(self.reg_lambda, tf.nn.l2_loss(self.V))) self.reg_loss = tf.add(self.l2_loss, self.reg) self.optimizer = tf.train.AdamOptimizer(self.learning_rate) self.train_step_u = self.optimizer.minimize(self.reg_loss, var_list=[self.U, self.U_bias]) self.train_step_v = self.optimizer.minimize(self.reg_loss, var_list=[self.V, self.V_bias]) tf.summary.scalar("RMSE", self.RMSE) tf.summary.scalar("MAE", self.MAE) tf.summary.scalar("L2-Loss", self.l2_loss) tf.summary.scalar("Reg-Loss", self.reg_loss) # add op for merging summary self.summary_op = tf.summary.merge_all() # add Saver ops self.saver = tf.train.Saver() def weight_variable(self, shape, name): initial = tf.truncated_normal(shape, stddev=0.001) return tf.Variable(initial, name=name) def bias_variable(self, shape, name): b_init = tf.constant_initializer(0.) return tf.get_variable(name, shape, initializer=b_init) def construct_feeddict(self, u_idx, v_idx, M): return {self.u_idx:u_idx, self.v_idx:v_idx, self.r:M[u_idx, v_idx]} def train_test_validation(self, M, train_idx, test_idx, valid_idx, n_steps=100000, result_path='result/'): nonzero_u_idx = M.nonzero()[0] nonzero_v_idx = M.nonzero()[1] train_size = train_idx.size trainM = np.zeros(M.shape) trainM[nonzero_u_idx[train_idx], nonzero_v_idx[train_idx]] = M[ nonzero_u_idx[train_idx], nonzero_v_idx[train_idx]] best_val_rmse = np.inf best_val_mae = np.inf best_test_rmse = 0 best_test_mae = 0 train_writer = tf.summary.FileWriter(result_path + '/train', graph=self.sess.graph) valid_writer = tf.summary.FileWriter(result_path + '/validation', graph=self.sess.graph) test_writer = tf.summary.FileWriter(result_path + '/test', graph=self.sess.graph) self.sess.run(tf.global_variables_initializer()) for step in range(1, n_steps): batch_idx = np.random.randint(train_size, size=self.batch_size) u_idx = nonzero_u_idx[train_idx[batch_idx]] v_idx = nonzero_v_idx[train_idx[batch_idx]] feed_dict = self.construct_feeddict(u_idx, v_idx, trainM) self.sess.run(self.train_step_v, feed_dict=feed_dict) _, rmse, mae, summary_str = self.sess.run( [self.train_step_u, self.RMSE, self.MAE, self.summary_op], feed_dict=feed_dict) train_writer.add_summary(summary_str, step) if step % int(n_steps / 100) == 0: valid_u_idx = nonzero_u_idx[valid_idx] valid_v_idx = nonzero_v_idx[valid_idx] feed_dict = self.construct_feeddict(valid_u_idx, valid_v_idx, M) rmse_valid, mae_valid, summary_str = self.sess.run( [self.RMSE, self.MAE, self.summary_op], feed_dict=feed_dict) valid_writer.add_summary(summary_str, step) test_u_idx = nonzero_u_idx[test_idx] test_v_idx = nonzero_v_idx[test_idx] feed_dict = self.construct_feeddict(test_u_idx, test_v_idx, M) rmse_test, mae_test, summary_str = self.sess.run( [self.RMSE, self.MAE, self.summary_op], feed_dict=feed_dict) test_writer.add_summary(summary_str, step) print("Step {0} | Train RMSE: {1:3.4f}, MAE: {2:3.4f}".format( step, rmse, mae)) print(" | Valid RMSE: {0:3.4f}, MAE: {1:3.4f}".format( rmse_valid, mae_valid)) print(" | Test RMSE: {0:3.4f}, MAE: {1:3.4f}".format( rmse_test, mae_test)) if best_val_rmse > rmse_valid: best_val_rmse = rmse_valid best_test_rmse = rmse_test if best_val_mae > mae_valid: best_val_mae = mae_valid best_test_mae = mae_test self.saver.save(self.sess, result_path + "/model.ckpt") return best_test_rmse, best_test_mae
以上就是基于用户行为显示数据的矩阵分解的分享。