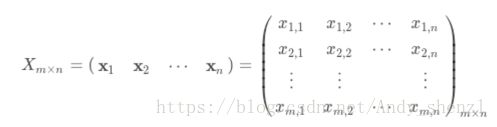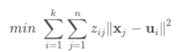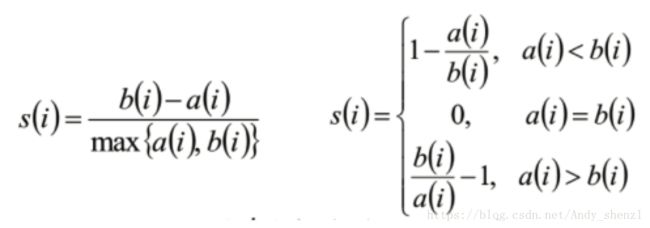K-means算法及python sklearn实现

目录

K-means算法

前言

K-Means算法的概述

K-Means算法的基本原理

K-Means与矩阵分解

实例推演

1、数据准备

2、随机选取重心

3、重新计算重心

4、重复计算

 K值的确定

聚类评估：轮廓系数（Silhouette Coefficient ）

k-means的优缺点

sklearn中对于kmeans算法的参数

sklearn实例实现

轮廓系数

---

K-means算法

前言

根据训练样本是否包含标签信息，机器学习可以分为监督学习和无监督学习。聚类算法是典型的无监督学习，其训练样本中只包含样本特征，不包含样本的标签信息。在聚类算法中，利用样本的特征，将具有相似属性的样本划分到同一类别中。

K-means算法，也被称为K-均值或K-平均算法，是一种广泛使用的聚类算法。K-means算法是基于相似性的无监督的算法，通过比较样本之间的相似性，将较为相似的样本划分到同一类别中。由于K-means算法简单、易于实现的特点， K-means算法得到了广泛的应用。

K-Means算法的概述

基本K-Means算法的思想很简单，事先确定常数K，常数K意味着最终的聚类类别数，首先随机选定初始点为质心，并通过计算每一个样本与质心之间的相似度(这里为欧式距离)，将样本点归到最相似的类中，接着，重新计算每个类的质心(即为类中心)，重复这样的过程，知道质心不再改变，最终就确定了每个样本所属的类别以及每个类的质心。由于每次都要计算所有的样本与每一个质心之间的相似度，故在大规模的数据集上，K-Means算法的收敛速度比较慢。

K-Means算法的基本原理

K-Means算法是较为经典的聚类算法，假设训练数据集X为：{x1,x2,⋯,xn}，其中，每一个样本xj为m维的向量。此时的样本为一个m×n的矩阵：

假设有k个类，分别为：{C1,⋯,Ck}。k-Means算法通过欧式距离的度量方法计算每一个样本xj到质心之间的距离，并将其划分到较近的质心所属的类别中并重新计算质心，重复以上的过程，直到质心不再改变为止，上述的过程可以总结为：

• 初始化常数K，随机选取初始点为质心
• 重复计算以下过程，直到质心不再改变

计算样本与每个质心之间的相似度，将样本归类到最相似的类中

重新计算质心

• 输出最终的质心以及每个类

K-Means与矩阵分解

K-Means的目标函数

最终使得质心不再改变，这就意味着每一个样本被划分到了最近的质心所属的类别中，即：

 

公式推到参见：https://blog.csdn.net/google19890102/article/details/51142299

实例推演

1、数据准备

下面我们用一个案例来看一下：

样本    X0    X1
1    7    5
2    5    7
3    7    7
4    3    3
5    4    6
6    1    4
7    0    0
8    2    2
9    8    7
10    6    8
11    5    5
12    3    7

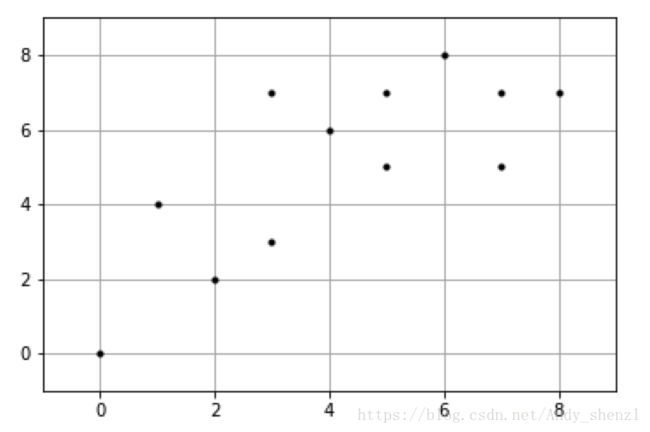
上表有两个解释变量，每个样本有两个特征。用python演示一下

%matplotlib inline
import matplotlib.pyplot as plt

import numpy as np
X0 = np.array([7, 5, 7, 3, 4, 1, 0, 2, 8, 6, 5, 3])
X1 = np.array([5, 7, 7, 3, 6, 4, 0, 2, 7, 8, 5, 7])
plt.figure()
plt.axis([-1, 9, -1, 9])
plt.grid(True)
plt.plot(X0, X1, 'k.')

2、随机选取重心

假设K-Means初始化时，随机设定两个重心，将第一个类的重心设置在第5个样本，第二个类的重心设置在第11个样本.那么我们可以把每个实例与两个重心的距离都计算出来，将其分配到最近的类里面。计算结果如下表所示：

样本	X0	X1	与C1距离	与C2距离	上次聚类结果	新聚类结果	是否改变
1	7	5	3.16	2.00	None	C2	YES
2	5	7	1.41	2.00	None	C1	YES
3	7	7	3.16	2.83	None	C2	YES
4	3	3	3.16	2.83	None	C2	YES
5	4	6	0.00	1.41	None	C1	YES
6	1	4	3.61	4.12	None	C1	YES
7	0	0	7.21	7.07	None	C2	YES
8	2	2	4.47	4.24	None	C2	YES
9	8	7	4.12	3.61	None	C2	YES
10	6	8	2.83	3.16	None	C1	YES
11	5	5	1.41	0.00	None	C2	YES
12	3	7	1.41	2.83	None	C1	YES
C1重心	4	6
C2重心	5	5

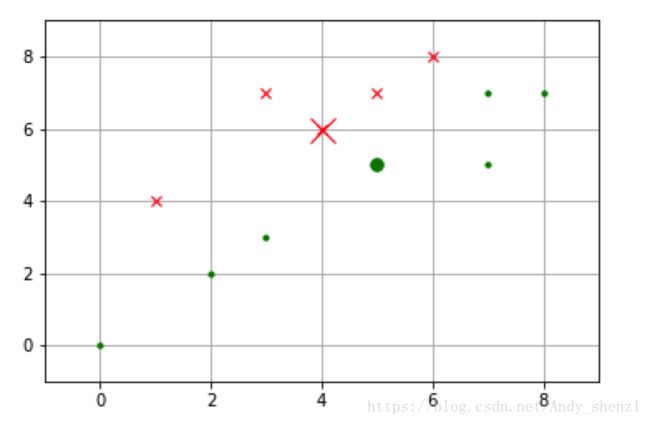
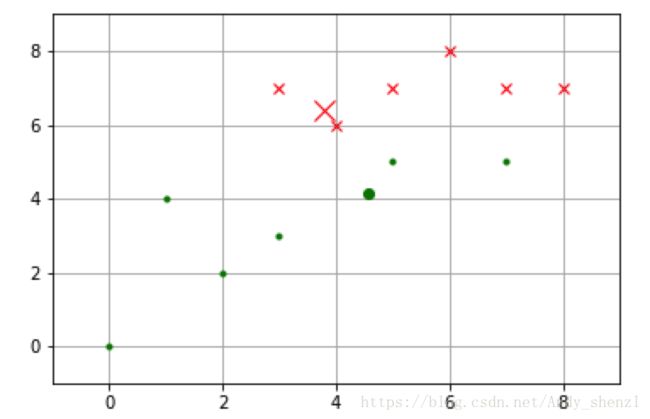
新的重心位置和初始聚类结果如下图所示。第一类用X表示，第二类用点表示。重心位置用稍大的点突出显示。

C1 = [1, 4, 5, 9, 11]#属于C1的index
C2 = list(set(range(12)) - set(C1))#属于C2的index
X0C1, X1C1 = X0[C1], X1[C1]#属于C1的坐标
X0C2, X1C2 = X0[C2], X1[C2]#属于C2的坐标
plt.figure()
plt.axis([-1, 9, -1, 9])
plt.grid(True)
plt.plot(X0C1, X1C1, 'rx')
plt.plot(X0C2, X1C2, 'g.')
plt.plot(4,6,'rx',ms=15.0)
plt.plot(5,5,'g.',ms=15.0)

3、重新计算重心

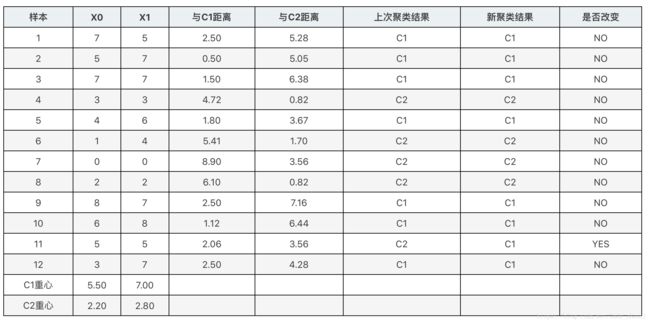
接下来我们需要重新计算两个类的重心，把重心移动到新位置，并重新计算各个样本与新重心的距离，并根据距离远近为样本重新归类。结果如下表所示： 

样本	X0	X1	与C1距离	与C2距离	上次聚类结果	新聚类结果	是否改变
1	7	5	3.49	2.58	C2	C2	NO
2	5	7	1.34	2.89	C1	C1	NO
3	7	7	3.26	3.75	C2	C1	YES
4	3	3	3.49	1.94	C2	C2	NO
5	4	6	0.45	1.94	C1	C1	NO
6	1	4	3.69	3.57	C1	C2	YES
7	0	0	7.44	6.17	C2	C2	NO
8	2	2	4.75	3.35	C2	C2	NO
9	8	7	4.24	4.46	C2	C1	YES
10	6	8	2.72	4.11	C1	C1	NO
11	5	5	1.84	0.96	C2	C2	NO
12	3	7	1.00	3.26	C1	C1	NO
C1重心	3.80	6.40
C2重心	4.57	4.14

C1 = [1, 2, 4, 8, 9, 11]
C2 = list(set(range(12)) - set(C1))
X0C1, X1C1 = X0[C1], X1[C1]
X0C2, X1C2 = X0[C2], X1[C2]
plt.figure()
plt.axis([-1, 9, -1, 9])
plt.grid(True)
plt.plot(X0C1, X1C1, 'rx')
plt.plot(X0C2, X1C2, 'g.')
plt.plot(3.8,6.4,'rx',ms=12.0)
plt.plot(4.57,4.14,'g.',ms=12.0)

4、重复计算

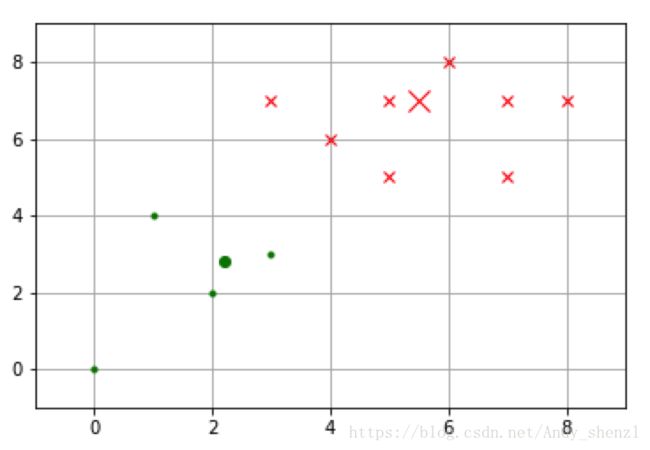
接下来再重复一次上面的做法，把重心移动到新位置，并重新计算各个样本与新重心的距离，并根据距离远近为样本重新归类。结果如下表所示：

C1 = [0, 1, 2, 4, 8, 9, 10, 11]
C2 = list(set(range(12)) - set(C1))
X0C1, X1C1 = X0[C1], X1[C1]
X0C2, X1C2 = X0[C2], X1[C2]
plt.figure()
plt.axis([-1, 9, -1, 9])
plt.grid(True)
plt.plot(X0C1, X1C1, 'rx')
plt.plot(X0C2, X1C2, 'g.')
plt.plot(5.5,7.0,'rx',ms=12.0)
plt.plot(2.2,2.8,'g.',ms=12.0)

再重复上面的方法就会发现类的重心不变了，K-Means会在条件满足的时候停止重复聚类过程。通常，条件是前后两次迭代的成本函数值的差达到了限定值，或者是前后两次迭代的重心位置变化达到了限定值。如果这些停止条件足够小，K-Means就能找到最优解。不过这个最优解不一定是全局最优解。 

局部最优解

前面介绍过K-Means的初始重心位置是随机选择的。有时，如果运气不好，随机选择的重心会导致K-Means陷入局部最优解。

K-Means最终会得到一个局部最优解，这些类可能没有实际意义，可能是更有合理的聚类结果。为了避免局部最优解，K-Means通常初始时要重复运行十几次甚至上百次。每次重复时，它会随机的从不同的位置开始初始化。最后把最小的成本函数对应的重心位置作为初始化位置。

 K值的确定

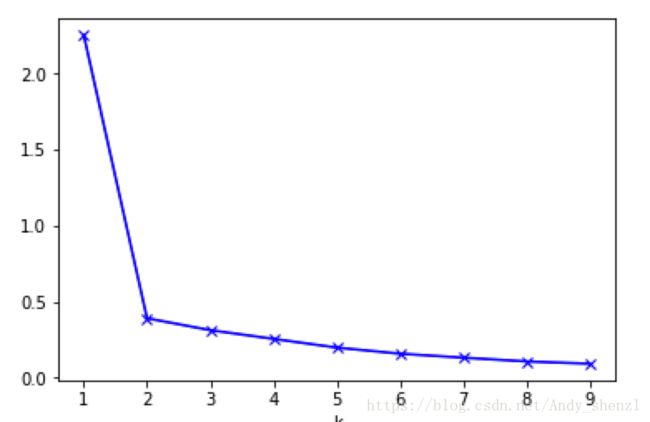
如果问题中没有指定的值，可以通过肘部法则这一技术来估计聚类数量。肘部法则会把不同值的成本函数值画出来。随着值的增大，平均畸变程度会减小；每个类包含的样本数会减少，于是样本离其重心会更近。但是，随着值继续增大，平均畸变程度的改善效果会不断减低。值增大过程中，畸变程度的改善效果下降幅度最大的位置对应的值就是肘部。下面让我们用肘部法则来确定最佳的值。

其中需要解释的一点是： 

每个类的畸变程度等于该类重心与其内部成员位置距离的平方和。也即我们前面所说的每个类的类内离差平方和。若类内部的成员彼此间越紧凑则类的畸变程度越小，反之，若类内部的成员彼此间越分散则类的畸变程度越大。

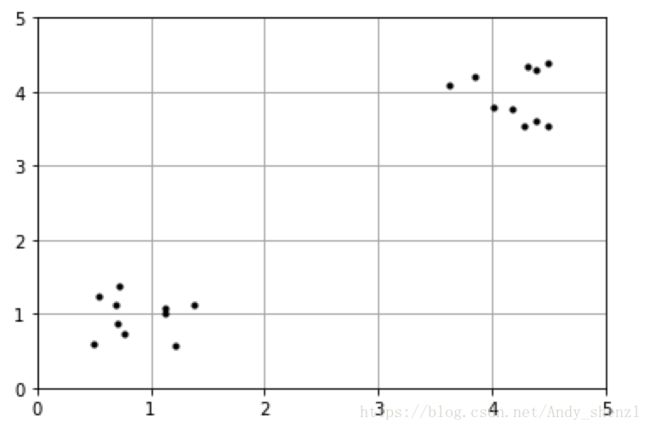
下图数据明显可分成两类：

import numpy as np
cluster1 = np.random.uniform(0.5, 1.5, (2, 10))
cluster2 = np.random.uniform(3.5, 4.5, (2, 10))
X = np.hstack((cluster1, cluster2)).T
plt.figure()
plt.axis([0, 5, 0, 5])
plt.grid(True)
plt.plot(X[:,0],X[:,1],'k.')

from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt 
K = range(1, 10)
meandistortions = []
for k in K:
    kmeans = KMeans(n_clusters=k)
    kmeans.fit(X)
    meandistortions.append(sum(np.min(cdist(X, kmeans.cluster_centers_, 'euclidean'), axis=1)) / X.shape[0])
plt.plot(K, meandistortions, 'bx-')
plt.xlabel('k')

聚类评估：轮廓系数（Silhouette Coefficient ）

• 计算样本i到同簇其他样本的平均距离ai。ai 越小，说明样本i越应该被聚类到该簇。将ai 称为样本i的簇内不相似度。
• 计算样本i到其他某簇Cj 的所有样本的平均距离bij，称为样本i与簇Cj 的不相似度。定义为样本i的簇间不相似度：bi =min{bi1, bi2, ..., bik}

• si接近1，则说明样本i聚类合理
• si接近-1，则说明样本i更应该分类到另外的簇
• 若si 近似为0，则说明样本i在两个簇的边界上。

import numpy as np
from sklearn.cluster import KMeans
from sklearn import metrics

plt.figure(figsize=(8, 10)) 
plt.subplot(3, 2, 1)
x1 = np.array([1, 2, 3, 1, 5, 6, 5, 5, 6, 7, 8, 9, 7, 9])
x2 = np.array([1, 3, 2, 2, 8, 6, 7, 6, 7, 1, 2, 1, 1, 3])
X = np.array(list(zip(x1, x2))).reshape(len(x1), 2)
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('test')
plt.scatter(x1, x2)
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k', 'b']
markers = ['o', 's', 'D', 'v', '^', 'p', '*', '+']
tests = [2, 3, 4, 5, 8]
subplot_counter = 1
for t in tests:
    subplot_counter += 1
    plt.subplot(3, 2, subplot_counter)
    kmeans_model = KMeans(n_clusters=t).fit(X)
    for i, l in enumerate(kmeans_model.labels_):
        plt.plot(x1[i], x2[i], color=colors[l], marker=markers[l],ls='None')
        plt.xlim([0, 10])
        plt.ylim([0, 10])
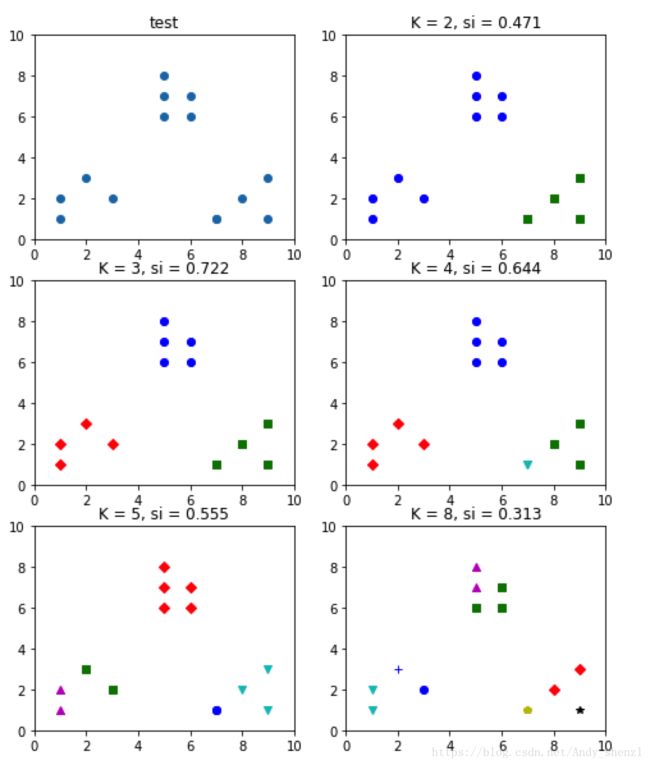
        plt.title('K = %s, si = %.03f' % (t, metrics.silhouette_score(X, kmeans_model.labels_,metric='euclidean')))

很显然，这个数据集包括三个类。在k=3的时候轮廓系数是最大的。在k=8的时候，每个类的样本不仅彼此很接近，而且与其他类的样本也非常接近，因此这时轮廓系数是最小的。 

k-means的优缺点

优点：

1、理解容易，聚类效果好；

2、处理大数据时，该算法可以保证较好的伸缩性和高效性；

3、当簇近似高斯分布时，效果很好

缺点：

1、K值需要自己设定，不同K值结果不同；

2、对于初试设定的重心非常敏感；

3、不适合发现非凸形状的簇或者大小差别较大的簇

4、特殊值(离群值)对模型的影响较大

https://www.naftaliharris.com/blog/visualizing-k-means-clustering/

这个网址可以展现聚类可视化的的过程，大家可以参考。

本次K-means主要是对表十大数据挖掘算法，所以不展开讲，之后会对K-means的延伸算法包括K-means++、MiniBatchKMeans、K-Mediods等进行讲解

sklearn中对于kmeans算法的参数

参数：

n_clusters：整形，缺省值=8 【生成的聚类数，即产生的质心（centroids）数。】 
max_iter：整形，缺省值=300 
执行一次k-means算法所进行的最大迭代数。 
n_init：整形，缺省值=10 
用不同的质心初始化值运行算法的次数，最终解是在inertia意义下选出的最优结果。 
init：有三个可选值：’k-means++’， ‘random’，或者传递一个ndarray向量。 
此参数指定初始化方法，默认值为 ‘k-means++’。 
（１）‘k-means++’ 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛
（２）‘random’ 随机从训练数据中选取初始质心。 
（３）如果传递的是一个ndarray，则应该形如 (n_clusters, n_features) 并给出初始质心。 
precompute_distances：三个可选值，‘auto’，True 或者 False。 
预计算距离，计算速度更快但占用更多内存。 
（１）‘auto’：如果 样本数乘以聚类数大于 12million 的话则不预计算距离。This corresponds to about 100MB overhead per job using double precision. 
（２）True：总是预先计算距离。 
（３）False：永远不预先计算距离。 
tol：float形，默认值= 1e-4　与inertia结合来确定收敛条件。 
n_jobs：整形数。　指定计算所用的进程数。内部原理是同时进行n_init指定次数的计算。 
（１）若值为 -1，则用所有的CPU进行运算。若值为1，则不进行并行运算，这样的话方便调试。 
（２）若值小于-1，则用到的CPU数为(n_cpus + 1 + n_jobs)。因此如果 n_jobs值为-2，则用到的CPU数为总CPU数减1。 
random_state：整形或 numpy.RandomState 类型，可选 
用于初始化质心的生成器（generator）。如果值为一个整数，则确定一个seed。此参数默认值为numpy的随机数生成器。 
copy_x：布尔型，默认值=True 
当我们precomputing distances时，将数据中心化会得到更准确的结果。如果把此参数值设为True，则原始数据不会被改变。如果是False，则会直接在原始数据 
上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算，所以数据返回后，原始数据和计算前可能会有细小差别。

属性：

cluster_centers_：向量，[n_clusters, n_features] (聚类中心的坐标)

Labels_: 每个点的分类 
inertia_：float形 
每个点到其簇的质心的距离之和。 

Notes： 
　　这个k-means运用了 Lioyd’s 算法,平均计算复杂度是 O(k*n*T)，其中n是样本量，T是迭代次数。 
　　计算复杂读在最坏的情况下为 O(n^(k+2/p))，其中n是样本量，p是特征个数。(D. Arthur and S. Vassilvitskii, ‘How slow is the k-means method?’ SoCG2006） 
　　在实践中，k-means算法时非常快的，属于可实践的算法中最快的那一类。但是它的解只是由特定初始值所产生的局部解。所以为了让结果更准确真实，在实践中要用不同的初始值重复几次才可以。

Methods：

fit(X[,y]): 
　计算k-means聚类。 
fit_predictt(X[,y]): 
　计算簇质心并给每个样本预测类别。 
fit_transform(X[,y])： 
计算簇并 transform X to cluster-distance space。 
get_params([deep])： 
　取得估计器的参数。 
predict(X):predict(X) 
　给每个样本估计最接近的簇。 
score(X[,y]): 
　计算聚类误差 
set_params(**params): 
　为这个估计器手动设定参数。 
transform(X[,y]): 将X转换为群集距离空间。 
　在新空间中，每个维度都是到集群中心的距离。 请注意，即使X是稀疏的，转换返回的数组通常也是密集的。

 

sklearn实例实现

我们还是基于上面推倒的数据案例：

import numpy as np
X0 = np.array([7, 5, 7, 3, 4, 1, 0, 2, 8, 6, 5, 3])
X1 = np.array([5, 7, 7, 3, 6, 4, 0, 2, 7, 8, 5, 7])

X = np.array(list(zip(X0, X1))).reshape(len(X0), 2)#压缩数据整合在一起

from sklearn.cluster import KMeans#导入KMeans包
km = KMeans(n_clusters=2).fit(X)#按照k=2进行计算

接下来我们看下结果：

km.labels_

out:array([0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0], dtype=int32)


centroids = km.cluster_centers_
print(centroids)

out:
[[5.625 6.5  ]
 [1.5   2.25 ]]

import matplotlib.pyplot as plt 
plt.figure()
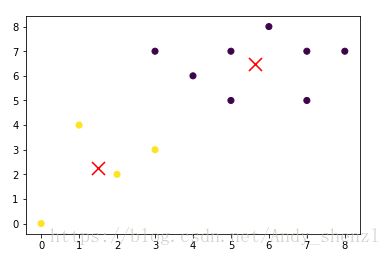
plt.scatter(X[:, 0], X[:, 1], c=km.labels_)#原始数据散点图，按照分类查看
centroids = km.cluster_centers_
plt.scatter(centroids[:, 0], centroids[:, 1],
            marker='x', s=169, linewidths=3,
            color='r', zorder=10)#重心红色X进行突出

轮廓系数

from sklearn.cluster import KMeans
from sklearn import metrics

scores = []
for k in range(2,12):
    labels = KMeans(n_clusters=k).fit(X).labels_
    score = metrics.silhouette_score(X, labels)
    scores.append(score)

scores

out:
[0.5438942330933946,
 0.3842109168420305,
 0.355936245851519,
 0.32130908377531114,
 0.29601716489116875,
 0.2552005855998481,
 0.19930860195228847,
 0.15131817710529702,
 0.07047330194279122,
 0.07047330194279122]