“容斥原理及其应用”笔记

容斥原理

举例

对{1, 2, … , n}的排列i₁, i₂, … , i_n计数，其中1不在第1个位置上（即i₁ ≠ 1）

已知1在第一个位置上的排列数和{2, 3, … , n}的排列数 (n−1)! 相同，而{1, 2, … , n}的排列总数为 n! 。因此 1 不在第一个位置的{1, 2, … , n} 排列个数有 (n−1)!(n−1) 个。

这个例子得出的直接计数的法则如下。如果A是集合S的子集，那么A中元素的个数等于S的元素的个数减去不在A中的元素的个数。令

A¯={x:x在S中，但x不在A中}

为A在S中的补，即由S的所有不在A中的元素组成的集合。该法则也可以写作

|A|=|S|−|A¯|或等价的|A¯|=|S|−|A|

这个公式的容斥原理最简单的例子。

含义

令S是物体的有限集，并令P₁、P₂ 是S中每个物体可能具有或者不具有的两性质。现在我们想要计算S中既不具有性质P₁ 又不具有性质 P₂ 的物体的个数。

通过这样一个过程可以得到：首先数出S中元素的个数，然后排除具有性质 P₁ 的元素，再排除具有性质 P₂ 的元素，这样同时具有P₁、P₂ 性质的元素排除 了两次，故需要再数回一次。这是我们有

|P¯1∩P¯2|=|S|−|P1|−|P2|+|P1∩P2|

定义

集S的不具有性质P₁， P₂， … , P_n 的物体的个数由下述公式给出：

|P¯1∩P¯2∩...∩P¯n|=|S|−∑|Pi|+∑|Pi∩Pj|−∑|Pi∩Pj∩Pk|+...+(−1)m|P1∩P2∩...∩Pm|

其中，第一个和对{1, 2, … , n}中的1-组合 {i} 进行，第二个和对 {1, 2, … , n}中的所有 2-组合 {i, j} 进行，第三个和对{1, 2, … , n} 的所有3-组合进行等等。

举例子，如果m = 3，上式变成

|P¯1∩P¯2∩...∩Pn|=|S|−(|P1|+|P2|+|P3|)+(|P1∩P2|+|P1∩P3|+|P2∩P3|)−|P1∩P2∩P3|

上式右边共有8项，当m = 4时，上式右边就会有16项。一般情况下，上式右边的项数为

C(m,1)+C(m,2)+...+C(m,m)=2m

推论

至少具有性质P₁ , P₂ , … , P_m 之一的集合S的元素个数由

|P1∩P2∩...∩pm|=∑|Pi|−∑|Pi∩Pj|+∑|Pi∩Pj∩Pk|+...+(−1)m+1|P1∩P2∩...∩Pm|

其中求和的含义与容斥原理的定义相同。

具有重复的组合

由“排列与组合”笔记 我们可以知道n个不同元素的r-组合的数目为

C(n,r)=n!r!(n−r)!

并且可以证明就有k种不同物体且每种物体有无限重数的r-组合个数为

C(r+k−1,r)

本节通过一个例子利用容斥原理给出对于其充数没有限制的多重集的r-组合的个数计算方法，并且该方法对于一半情形仍然有效。

例 确定多重集 T = {3·a, 4·b, 5·c} 的10-组合个数。

我们将容斥原理运用于多重集T* = {∞·a, ∞·b, ∞·c} 的所有10-组合的集合S上。令P₁为T*的10-组合具有多于3个a的性质，P₂ 为T*的10-组合具有多余4个b的性质，P₃ 为T*的10-组合具有多余5个c的性质。此时T的10-组合就是T*中不具有P₁, P₂, P₃ 的10-组合个数。同样令 Ai 由T* 的具有性质P_i （i = 1， 2， 3）的哪些10-组合构成。我们希望确定集合 A¯1∩A¯2∩A¯3 的大小。由容斥原理

|A¯1∩A¯2∩A¯3|=|S|−(|A1|+|A2|+|A3|)+(|A1∩A2|+|A1∩A3|+|A2∩A3|)−(A1∩A2∩A3)

由上面的预备知识可以知道

|S|=C(10+3−1，10)=C(12,2)=66

集合A₁ 由a至少出现4次的T* 的所有10-组合构成。如果拿出A₁ 的任一这样的10-组合并去掉4个a，那么剩下的就是T* 的一个6-组合。反之，如果拿出一个T* 的一个6-组合，并向其中添加4个a，就得到T* 的一个10-组合，并且这个10-组合a至少出现4次。这样A₁ 中的10-组合个数就等于T* 的6-组合的个数。因此

|A1|=C(6+3−1,6)=C(8,2)=28

类似地，A₂ 中的10-组合个数和T* 中的5-组合个数相等，A₃中的10-组合个数和T* 的6-组合个数相等。于是有

|A2|=C(5+3−1,5)=C(7,2)=21

|A3|=C(6+3−1,6)=C(6,2)=15

集合A₁ ∩ A₂ 由a至少出现4次和b至少出现5次的T*的所有10-组合个数相等。如果从这些10-组合中去掉4个a和5个b，则剩下T* 的1-组合。反之，如果往T*的1-组合中添加4个a和5个b，就能得到一个10-组合，并且在这个组合中a至少出现4次，b至少出现5次。这样，在A₁ ∩ A₂ 中的10-组合个数就等于T*中的1-组合个数，即：

|A1∩A2|=C(1+3−1,1)=C(3,1)=3

同理可得到A₁ ∩ A₃ 中的10-组合个数等于T*中的0-组合个数，而且，在A₂ ∩ A₃ 中没有10-组合。于是

|A1∩A3|=C(0+3−1,0)=C(2,0)=1

及

|A2∩A3|=0

还有

|A1∩A2∩A3|=0

将这些结果放在容斥原理中得到：

|A¯1∩A¯2∩A¯3|=66−(28+21+15)+(3+1+0)−0=6

以上方法对一般的有限多重集组合仍然适用，所以不失一般性地，运用容斥原理可以很好地解决有限多重集组合问题。

错位排列

举例

在一个聚会中，8位绅士查看他们的帽子。有多少种方法使得这些绅士没有人能够拿到他们来时所戴的帽子？

V-8发动机的8个火花塞从气缸中被拔出来清洗，有多少种方式能将它们放回气缸时使得没有火花塞重新放回到原先被取出时的气缸？

含义

取X为集合{1, 2, … , n}, 其中每个整数的位置都由它们在序列1，2，… , n中的位置确定。{1, 2, … , n}的一个错位排列是{1, 2, … , n}的一个排列i₁i₂…i_n， 使得i₁ ≠ 1， i₂ ≠ 2 ，… , i_n ≠ n 。因此， {1, 2, … , n}的一个错位排列是{1, 2, … , n}的一个排列i₁i₂…i_n，在这个排列中没有整数在自然的位置上：i₁ ≠ 1， i₂ ≠ 2 ，… , i_n ≠ n。

定理及其计算

用 Dn 表示{1, 2, … , n}的错排个数。对于 n ≥ 1，

Dn=n!(1−11!+12!−13!+…+(−1)n1n!)

因为 e−1 的级数展开式

e−1=1−11!+12!−13!+14!…

所以

e−1=Dnn!+(−1)n+11(n+1)!+(−1)n+21(n+2)!+⋯

从无穷交错级数可以断定， e−1 和 Dn/n! 相差小于 1/(n+1)! ; 事实上， Dn 是最接近 n!/e 的整数。

错排还满足一些便于求值的关系式。第一个如下：

Dn=(n−1)(Dn−1+Dn−2),(n=3,4,5,⋯)

由初始信息 D1=0,D2=1 出发， 我们可以使用上式计算对于任意正整数 n 的 Dn

第二个可由第一个递归推得：

Dn=nDn−1+(−1)n−2

或等价地

Dn=nDn−1+(−1)n(n=2,3,4,⋯)

带有禁止位置的排列

含义

这一节我们考虑计算{1, 2, … , n} 的一般带有限制的排列计数问题，这些限制规定在每个排列的位置上都能够由哪些整数占据。

令

X1,X2,⋯,Xn

是{1, 2, … , n}的子集（可以为空集）。用

P(X1,X2,...,Xn)

表示{1, 2, … , n}的所有排列 i1i2⋯in 的集合，使得i₁ 不在 X₁内， i₂ 不在X₂ 内，… , i_n 不在X_n 内

如果{1, 2, … , n}的一个排列使得 X1 的元素不占据该排列第一个位置(这样一来，能够唯一第一个位置上的元素是那些在 X1 的补 X¯1 的元素)， X2 的元素不占据该排列第二个位置， … , Xn 的元素不占据该排列第n个位置，则该排列属于集 P(X1,X2,⋯,Xn) 的排列的个数是

p(X1,X2,⋯,Xn)=|P(X1,X2,...Xn)|

表示。

计算方法及其定理

已知，在 {1, 2, … , n} 的排列和n行n列棋盘上非攻击型不可区分的车的位置之间存在一一对应。{1, 2, … , n} 。{1, 2, … , n} 的排列 i1i2⋯in 以坐标为 (1,i1),(2,i2),⋯,(n,in) 对应棋盘上n个位置。在 P(X1,X2,⋯,Xn) 内的排列对应着n排n列n个非攻击型车的摆放，但是在这个棋盘上有某些放个禁止放车。

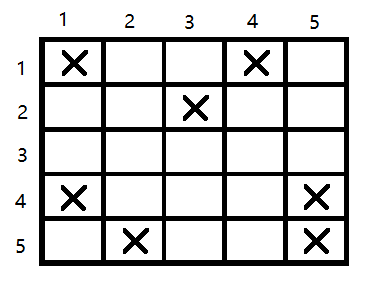
例 令n = 5, X₁ = {1, 4} , X₂ = {3}, X₃ = ∅， X₄ = {1， 5}， X₅ = {2，5}。则 P(X1,X2,X3,X4,X4) 中的排列一一对应具有如下图所示禁止位置的棋盘上的5个非攻击型车的位置。

为了方便，下面的论证将用n行n列棋盘上非攻击型车的语言叙述。

令S为n行n列棋盘上n个非攻击型车的所有 n! 中放置方法的集合。如果在第 j 行上的车是属于 Xj 的列上，那么我们就说n个非攻击型车的这样一种放置满足性质 Pj(j=1,2,...,n) 的车的放置集合。集合 P(X1,X2,⋯,Xn) 由n个车的所有不满足性质 P1,P2,⋯,Pn 的放置方法组成。 因此

p(X1,X2,...,Xn)=|A¯1∩A¯2∩⋯∩A¯n|=n!−∑|Ai|+∑|Ai∩Aj|−⋯+(−1)k∑|Ai1∩Ai2∩⋯∩Aik|+⋯+∑A1∩A2∩⋯∩An|

其中，第k个和是对{1, 2, … , n} 的所有k-组合求和。现在我们计算上述公式中的n个和的值。例如 |A1| 的计数是多少？ 它是把n个非攻击型车放在棋盘上，其中第一行的车要放在位于 X1 的一个列上。我们能够以 |X1| 种方式选择该车的列，然后以 (n−1)! 方式安置其余(n-1)个非攻击型车。于是 |A1|=|X1|(n−1)!(n=1,2,...,n) , 而且，更一般地有

|Ai|=|Xi|(n−1)!(i=1,2,⋯,n)

因此，

∑|Ai|=∑|Xi|(n−1)!

令 r1=|X1|+|X2|+⋯+|Xn| , 得到

∑|Ai|=r1(n−1)!

数 r1 等于棋盘上禁止放车的方格数。等价地， r1 等于将一个棋盘上的车放在禁止放置的方格内的方法。

现在考虑 |A1∩A2| , 这个数表示的是将n个非攻击型车放在棋盘上的这样一种方法数，其中第一行和第二行的车都在禁止位置上(对应地在 X1 和 X2 内)。在第一行和第二方的禁止位置上放置好非攻击型车后，剩余的车可以以 (n−2)! 中方法完成。类似地，考虑对于任意的 |Ai∩Aj| 也成立。令 r2 表示包两个非攻击型车放到棋盘禁止位置的方法数。则

∑|Ai∩Aj|=r2(n−2)!

可以直接推广上式并给上式中的第k个和式赋值。我们定义 rk 如下：

rk 是把k个非攻击型车放到n行n列棋盘上的这样一种方法数，其中这k个车中的每个都处在禁止放置的位置上 (k = 1, 2, … , n)

于是

∑|Ai1∩Ai2∩⋯∩Ain|=rk(n−k)!(k=1,2,...,n)

静上述公式代入求取 p(X1,X2,...,Xn) 的等式，则有下面的定理：

定理 将n个非攻击型不可区分的车放到带有禁止位置的n行n列棋盘上的放置方法数等于

n!−r1(n−1)!+r2(n−2)!−r3(n−3)!+⋯+(−1)krk(n−k)!+⋯+(−1)nrn

以上です。