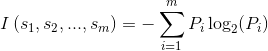数据分析笔试错题要点及解析

1、为数据的总体分布建模，把多维空间划分成组等问题，属于数据挖掘中的哪一类任务：建模描述

2、假设12个销售价格记录组已经排序如下：5, 10, 11, 13, 15,35, 50, 55, 72, 92, 204, 215 使用如下每种方法将它们划分成四个箱。等频（等深）划分时，15在第几个箱子内？ ：第二个

   解析：

            连续属性离散化有三种常用方法：

                     等宽法：将属性的值域分成具有相同宽度的区间，区间的个数由数据本身的特点决定。

                     等频法：将相同数量的记录放进每个区间。

                     基于聚类分析的方法：需要用户指定簇的个数，从而决定产生的区间数。

3、数据的属性类型：

标称属性(nominal attribute)的值是一些符号或事物的名称。 标称属性是定性数据，不能进行定量计算。

二元属性(binary attribute)是一种标称属性，只有两个类别或状态：0和1，其中0通常表示该属性不出现，而1表示出现。二元属性又称布尔属性，如果两种状态对应于true和false的话。

•        一个二元属性是对称的，如果它的两种状态具有相同价值并且携带相同的权重；即，关于哪个结果应该用0或1编码并无偏好。比如性别。
•         一个二元属性是非对称的，如果其状态的结果不是同样重要的，比如艾滋病毒化验的阳性和阴性结果。

序数属性(ordinal attribute)，其可能的值之间具有有意义的序或秩评定(ranking)，但是相继值之间的差是未知的。比如，成绩有A+, A, A-, B+, B等。

数值属性(numeric attribute)是定量的，即它是可度量的量，用整数或实数值表示。 数值属性可分为区间标度或比率标度的。

离散属性、连续属性

4、只有非零值才重要的二元属性被称为：非对称的二元属性

5、不属于创建新属性的相关方法的是：B

   A 特征提取

  B 特征修改

  C 映射数据到新的空间

  D 特征构造

 解析：  属性创建也称特征创建，包括特征提取、映射数据到新的空间（傅利叶变换、小波变换）、二次特征（特征构造）

6、考虑值集{1、2、3、4、5、90}，其截断均值（p=20%）是 ：3.5

    解析：截断均值：除去两端的百分率为p的数据，对剩下的数据计算均值。   

              6×p=1.2，两端各去掉一个数， 除去1和90，均值为3.5。

7、下面哪个属于映射数据到新的空间的方法：傅利叶变换

     解析：特征创建包括特征提取、映射数据到新的空间（傅利叶变换、小波变换）、二次特征（特征构造）

8、 熵是为消除不确定性所需要获得的信息量，投掷均匀正六面体骰子的熵是：2.6比特

     解析：信息熵的计算公式：

        

  

9、假定用于分析的数据包含属性age。数据元组中age的值如下（按递增序）：13，15，16，16，19，20，20，21，22，22，25，25，25，30，33，33，35，35，36，40，45，46，52，70, 问题：使用按箱平均值平滑方法对上述数据进行平滑，箱的深度为3。第二个箱子值为   ：18.3

解析：（个人理解）i=i+3，所以每三个一组，按照大小排序，第二组是（16,19,20），亲测第二组的均值是18.3

参考链接：https://www.wesiedu.com/zuoye/6061468502.html

 

10、考虑值集{12 , 24 , 33, 2 , 4 , 55 , 68 , 26}，其四分位数极差是 ：

解析：上四分位数为：L= 8×0.75=7，取为 L与(L+1) 的均值，按从小到大的顺序排列，第六的数值是33，第七的是55，均值是44，即=44

            下四分位数为：L=8×0.25=2，取为 L与(L+1) 的均值，第二的数值是4，第三的是12，均值是8，即=8

             四分位差为：44-8=36

 

若题目的值集为：{12 , 24 , 33, 24 , 55 , 68 , 26}，其四分位数极差是 ：31

           上四分位数为：L= 7×0.75=5.25，取为 (L+1) =6，按从小到大的顺序排列，第六的数值是55，即=55

            下四分位数为：L=7×0.25=1.75，取为 (L+1) =2，第二的数值是24，即=24

             四分位差为：55-24=31

参考链接：https://blog.csdn.net/pipisorry/article/details/72820982

 

11、众数：出现最多次的观测值

12、下列哪个不是专门用于可视化时间空间数据的技术：B

A等高线图

B饼图

C曲面图

D矢量场图

13、在抽样方法中，当合适的样本容量很难确定时，可以使用的抽样方法是：D

A有放回的简单随机抽样

B无放回的简单随机抽样

C分层抽样

D渐进抽样

解析：分层抽样：当分析需要所有类型的代表时

14、基本元数据包括关于装载和更新处理,分析处理以及管理方面的信息

15、数据越详细,粒度就越小,级别也就越高

16、OLAP技术的核心是多维分析

 

机器学习中L1正则化和L2正则化的区别是：使用L1可以得到稀疏的权值，使用L2可以得到平滑的权值

Logistic regression：L1正则能够使权重稀疏，这样参数值就受到控制会趋近于0。L1正则还被称为 Lasso regularization

L1范数是指向量中各个元素绝对值之和，用于特征选择

L2范数 是指向量各元素的平方和然后求平方根，用于 防止过拟合，提升模型的泛化能力

sigmoid在逻辑回归中起到了两个作用，一是将线性函数的结果映射到了(0,1)，一是减少了离群点的影响

SPSS的界面中，主窗口是数据编辑窗口。数据整理的功能主要集中在数据和转换等菜单中，分析菜单中没有。

主变量分析就是 K-L 变换。K-L变换的突出优点是去相关性好，是均方误差（MSE，Mean Square Error）意义下的最佳变换，它在数据压缩技术中占有重要地位

SVM 常用核函数：线性核函数、多项式核函数、高斯（RBF）核函数（高斯径向基函数）、sigmoid 核函数

k-NN最近邻方法在( )的情况下效果较好：样本较少，但典型性好