图卷积网络详细介绍

声明：本文翻译自Tobias Skovgaard Jepsen写在Medium上的博客文章，已获得其本人的许可；版权归原作者所有，未经同意请勿转载；文中带有“注”标记的内容为本人添加，以便阅读。
原文链接：https://towardsdatascience.com/how-to-do-deep-learning-on-graphs-with-graph-convolutional-networks-7d2250723780

---

---

原标题：如何用图卷积网络在图上进行深度学习

第一部分 图卷积网络的高级介绍

在图上进行机器学习是一项困难的任务，因为它的复杂性很高，同时也是由于信息丰富的图结构。这篇文章是关于如何用图卷积网络(GCNs)对图进行深度学习的系列文章中的第一篇。GCNs是一种强大的神经网络，旨在直接处理图并利用它们的结构信息。

在这篇文章中，我将介绍GCNS，并通过编码示例说明如何通过GCN的隐藏层传播信息。我们将看到GCN如何从前面的层聚合信息，以及这种机制如何生成图中节点的有用的特征表示。

图卷积网络是什么？

GCNs是一种非常强大的在图上进行机器学习的神经网络框架。事实上，它们是如此强大，以至于即使是随机初始化的2层GCN也可以生成网络中节点的有用的特征表示。下图显示了这样一个GCN是如何生成一个网络中每个节点的二维表示的，它可以在不经过任何训练的情况下保持它们在网络中的相对接近性。

更正式地说，图卷积网络(GCN)是一种在图上操作的神经网络。
给定一个图 $G=(E,V)$， 一个GCN的输入如下：

• 一个$N\times F^0$的输入特征矩阵$X$，其中$N$是图中的节点个数，$F^0$是每个节点的输入特征个数；
• 一个$N\times N$的图结构表示矩阵，比如$G$的邻接矩阵$A$。

因此，GCN中的隐藏层可以写成$H^i=f(H^{i-1},A)$，其中$H^0=X$，$f$是传播函数 [1]。每层$H^i$对应于$N\times F^i$ 特征矩阵，其中每一行是节点的特征表示。在每一层，这些特征被聚合后再用传播规则$f$形成下一层的特征。这样，特征在每一个连续的层上都变得越来越抽象。在这个框架中，GCN的变体仅在传播规则$f$ [1]的选择上有所不同。

一个简单的传播规则

最简单的传播规则之一如下：
$$f(H^i,A)=\sigma (A{H}^i{W}^i)$$
其中$W^i$是$i$层的权重矩阵，$\sigma$是一个非线性激活函数，如 $\mathbf{r}\mathbf{e}\mathbf{l}\mathbf{u}$ 函数。权重矩阵具有维数$F^i\times F^{i+1}$；换句话说，权重矩阵第二维的大小决定下一层的特征个数。如果您熟悉卷积神经网络，则此操作类似于滤波操作，因为这些权重在图中的节点间是共享的。

简化

我们先从最简单的情况看一下传播规则，令

• $i=1$，那么$f$就是输入特征矩阵的一个函数；
• $\sigma$是恒等函数；
• 选择权重，也就是$A{H}^0{W}^0=AX{W}^0=AX$.

换句话说，$f(X,A)=AX$。这个传播规则可能太简单了，但是我们稍后会添加缺少的部分。另外，$AX$现在相当于多层感知器的输入层。

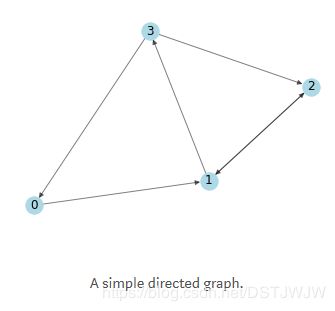
一个简单的图

下面的图是一个简单的例子：

上图的邻接矩阵为：

A = np.matrix([
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 1, 0, 0],
[1, 0, 1, 0]],
dtype=float
)

（注：上图是一个有向无权图，边可以是单方向的，如 $0\to 1$，可以也是双向的，如 $1\leftarrow \to 2$；图的邻接矩阵表示了图中的连接情况，如上面的矩阵中，第一行就表示第一个节点（对应图中的 $0$号节点，简称节点0，下同）的连边情况，其中第二个元素为1表示有一条从第一个节点指向第二个节点（节点1）的边，没有边则对应元素为0；注意本例中只将从某节点出发指向其他节点的边表示在邻接矩阵中，从其他节点指向该节点的边不表示，默认为0，如 $3\to 0$ 在矩阵中对应的元素为第四行第一列，而第一行第四列元素为0，换句话说，节点0是节点3的邻居节点，但是节点3却不是节点0的邻居节点，节点0只有一个邻居节点就是节点1.）

接下来，我们需要特征！我们根据每个节点的索引为其生成2个整数特征。这使得以后很容易手动确认矩阵计算。

In [3]: X = np.matrix([
            [i, -i]
            for i in range(A.shape[0])
        ], dtype=float)
        X
Out[3]: matrix([
           [ 0.,  0.],
           [ 1., -1.],
           [ 2., -2.],
           [ 3., -3.]
        ])

应用传播规则

好吧！现在我们有了一个图，它的邻接矩阵$A$和一组输入特征$X$。让我们看看当我们应用传播规则时会发生什么：

In [6]: A * X
Out[6]: matrix([
            [ 1., -1.],
            [ 5., -5.],
            [ 1., -1.],
            [ 2., -2.]]

看看发生了什么?每个节点(每一行)的表示现在是其邻居特征的总和！换句话说，图卷积层将每个节点表示为其邻域的集合。我鼓励你自己检查计算结果。注意，在这种情况下，如果存在从$v$到$n$的边，节点$n$就是节点$v$的邻居。（注：如第二行元素为5，就是节点1的两个邻居节点2和3的特征值之和.）

问题来了！！

可能你已经发现了问题：

• 节点的聚合表示不包括它自己的特征！这个表示只是其邻居节点特征的集合，因此只有具有自环的节点才会在聚合中包含自己的特征(除非节点具有自环)。[1]
• 大度的节点在特征表示中会有较大的值，而小度的节点将具有较小的值。这可能导致渐变[1, 2]消失或爆炸，但随机梯度下降算法也有问题，这些算法通常用于训练这类网络，并且对每个输入特征的尺度(或取值范围)敏感。

（注：自环指某节点有自己指向自己的边；在简单有向图中，度表示从某节点出发的边数，或者说其邻居节点的个数.）

下面，我将分别讨论这些问题。

添加自环

为了解决第一个问题，可以简单地向每个节点[1, 2]添加一个自环。在实践中，这是通过在应用传播规则之前将恒等矩阵 $I$ 添加到邻接矩阵 $A$ 来实现的。

In [4]: I = np.matrix(np.eye(A.shape[0]))
        I
Out[4]: matrix([
            [1., 0., 0., 0.],
            [0., 1., 0., 0.],
            [0., 0., 1., 0.],
            [0., 0., 0., 1.]
        ])
In [8]: A_hat = A + I
        A_hat * X
Out[8]: matrix([
            [ 1., -1.],
            [ 6., -6.],
            [ 3., -3.],
            [ 5., -5.]])

由于节点现在成了自己的邻居，所以在加和其邻居节点的特征时，节点本身的特征也包括在内！

特征表示归一化

通过将邻接矩阵 $A$ 与节点的度矩阵 $D$ 的逆相乘，可以将特征表示按节点度进行归一化[1]。因此，我们的简化传播规则如下[1]：$$f(X,A)=D^{-1}AX$$

(注：节点的度矩阵是一个对角矩阵，对角线上元素即为该节点的邻居节点个数.)

看看会发生什么。先计算下度矩阵。

In [9]: D = np.array(np.sum(A, axis=1))    # 原文此处是按照列求和，计算得到的是入度矩阵；实际上根据上文的邻接矩阵，应该是按照行求和，得到出度矩阵，才符合题意，故后文都是采用出度矩阵进行计算，计算结果与原文稍有出入
        D = [x[0] for x in D]  
        D = np.matrix(np.diag(D))
        D
Out[9]: matrix([
            [1., 0., 0., 0.],
            [0., 2., 0., 0.],
            [0., 0., 1., 0.],
            [0., 0., 0., 2.]
        ])

在应用这个规则前，我们先看看对邻接矩阵 $A$ 进行变换后发生了什么。

# Before
A = np.matrix([
    [0, 1, 0, 0],
    [0, 0, 1, 1], 
    [0, 1, 0, 0],
    [1, 0, 1, 0]],
    dtype=float
)
# After
In [10]: D**-1 * A
Out[10]: matrix([
             [0. , 1. , 0. , 0. ],
             [0. , 0. , 0.5, 0.5],
             [0. , 1. , 0. , 0. ],
             [0.5, 0. , 0.5, 0. ]
])

观察到邻接矩阵的每一行中的权重(值)已被对应行的节点的度除了。我们再对变换后的邻接矩阵应用传播规则。

In [11]: D**-1 * A * X
Out[11]: matrix([
             [ 1. , -1. ],
             [ 2.5, -2.5],
             [ 1. , -1. ],
             [ 1. , -1. ]
         ])

并得到与相邻节点特征均值相对应的节点表示。这是因为(变换的)邻接矩阵中的权重对应于相邻节点特征的加权和。再次，我鼓励你们自己验证这一观察。

合并

我们现在将自环和归一化操作结合起来。此外，为了简化讨论，我们将重新引入先前丢弃的权重和激活函数。

添加权重

第一要务是运用权重。请注意，这里 $D\_hat$是 $A\_hat=A+I$ 的度矩阵，也就是具有自环的 $A$ 的度矩阵。

In [45]: W = np.matrix([
             [1, -1],
             [-1, 1]
         ])
         D_hat**-1 * A_hat * X * W
Out[45]: matrix([
            [ 1., -1.],
            [ 4., -4.],
            [ 3., -3.],
            [ 3.333333, -3.333333]
        ])

如果我们想降低输出特征表示的维数，我们可以减小权重矩阵W的大小：

In [46]: W = np.matrix([
             [1],
             [-1]
         ])
         D_hat**-1 * A_hat * X * W
Out[46]: matrix([[1.],
        [4.],
        [3.],
        [3.333333]]
)

添加激活函数

我们选择保留特征表示的维数，并应用 ReLU 激活函数。

In [51]: W = np.matrix([
             [1, -1],
             [-1, 1]
         ])
         relu(D_hat**-1 * A_hat * X * W)
Out[51]: matrix([[1., 0.],
        [4., 0.],
        [3., 0.],
        [3.333333, 0.]])

瞧！一个完整的隐藏层，包含邻接矩阵、输入特征、权重和激活功能！

回归现实

最后，我们可以在真实的图上应用一个图卷积网络。我将向你们展示如何生成在文章前面出现的这种特征表示。

Zachary’s Karate Club

Zachary的空手道俱乐部是一个常用的社交网络，节点代表空手道俱乐部的成员，边表示其相互之间的关系。当Zachary在研究空手道俱乐部时，管理员和教练之间发生了冲突，导致俱乐部分裂成两半。下面显示了该网络的图表示，并根据节点属于俱乐部的哪个部分做了标记。管理员和教练分别用 $A$和 $I$ 标记。

构建GCN

现在我们来建立图卷积网络。实际上我们不会训练网络，而只是随机地初始化它，以产生我们在这篇文章开始时看到的特征表示。我将使用Networkx（python中专门为复杂网络和图论研究开发的第三方库），它可以很方便地表示俱乐部的图结构，并计算 $A\_hat$ 和 $D\_hat$ 矩阵。

from networkx import to_numpy_matrix
zkc = karate_club_graph()
order = sorted(list(zkc.nodes()))
A = to_numpy_matrix(zkc, nodelist=order)
I = np.eye(zkc.number_of_nodes())
A_hat = A + I
D_hat = np.array(np.sum(A_hat, axis=1))
D_hat = [x[0] for x in D_hat]
D_hat = np.matrix(np.diag(D_hat))

接下来，随机初始化权重。

W_1 = np.random.normal(
    loc=0, scale=1, size=(zkc.number_of_nodes(), 4))
W_2 = np.random.normal(
    loc=0, size=(W_1.shape[1], 2))

堆栈GCN层。这里我们只使用单位矩阵作为特征表示，即每个节点被表示为一个独热编码（one-hot encoded）的分类变量。

def gcn_layer(A_hat, D_hat, X, W):
    return relu(D_hat**-1 * A_hat * X * W)
H_1 = gcn_layer(A_hat, D_hat, I, W_1)
H_2 = gcn_layer(A_hat, D_hat, H_1, W_2)
output = H_2

提取特征表示

feature_representations = {
    node: np.array(output)[node] 
    for node in zkc.nodes()}

瞧！特征表示将Zachary空手道俱乐部中的社团清楚地区分开了。我们还没开始训练呢！

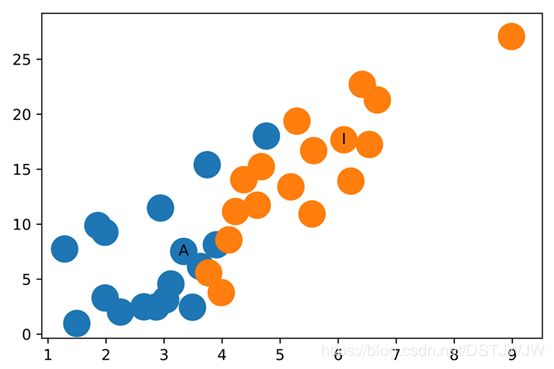
（注：在网络科学中，社团一般指网络中内部连接紧密外部连接稀疏的子网络；上图中，两个社团用不同的颜色表示出来，可以看到，两种颜色已经在很大程度上分离开了.）

应该注意到，在这个例子中，随机初始化权重很可能在x或y轴上出现0值，这是ReLU函数的结果，所以需要一些随机初始化来生成上面的数字。

结论

在这篇文章中，我给出了图卷积网络的高级介绍，并说明了GCN中每一层节点的特征表示是如何基于其邻域聚合的。我们看到了如何使用Numpy建立这些网络，以及它们的强大：即使是随机初始化的GCNs，也可以将Zachary空手道俱乐部中的社团分开。

在下一篇文章中，我将深入探讨一些技术细节，并介绍一些最近发表的GCNs。

参考文献

[1] Blog post on graph convolutional networks by Thomas Kipf.
[2] Paper called Semi-Supervised Classification with Graph Convolutional Networks by Thomas Kipf and Max Welling.