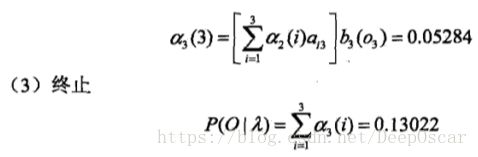一文看懂隐马尔科夫模型
隐马尔科夫模型(一)
万事不如先举个栗子:
假设有4个盒子,每个盒子里都有红白两种颜色的球,盒子里的红白球数如下:
按照下面的方法抽取球,缠身给一个球的颜色的观测序列:
①从4个盒子里以等概率随机选取1个盒子,从这个盒子里面随机抽出1个球,记录其颜色后,放回;
②从当前盒子随机转移到下一个盒子,规则是:如果当前盒子是盒子1,那么下一个盒子一定是2,如果当前盒子是2或3那么,分别以概率0.4和0.6转移到左边或右边的盒子,如果是盒子4,那么各以0.5的概率停留在盒子4或者转移到3;
③确定转移的盒子后,再从这个盒子里随机抽取1个球,记录其颜色,放回;
④重复5次,得到一个球的颜色观测序列
O = {红 红 白 白 红}
这个过程中,观察者智能观测到球的颜色的序列,观测不到球是从哪个盒子取出来的,即观测不到盒子的序列。
在这个例子中有两个随机序列,一个是盒子的序列(状态序列),一个是球的颜色的观测序列。前者是隐藏的,后这是可观测的。这是一个隐马尔科夫的例子。
因此,隐马尔科夫模型是可用于标注问题的统计学模型,描述由隐藏的马尔科夫链随机生成观测序列的过程,属于生成模型。
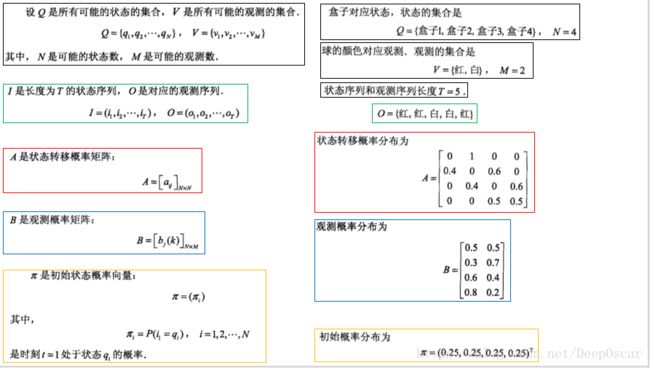
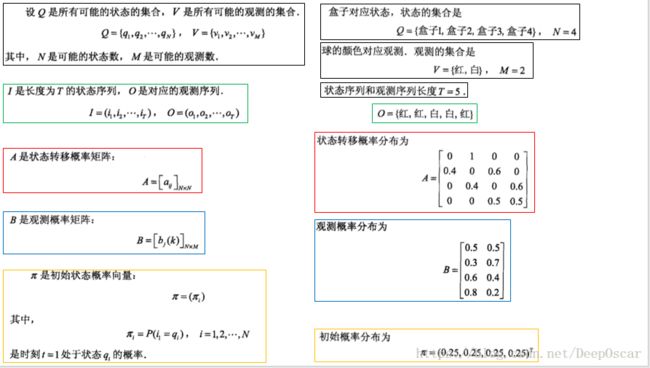
根据以上栗子,可以明确状态集合、观测集合、序列长度以及模型的三要素:
盒子对应的状态,状态集合为:
球的颜色对应观测,观测的集合为:
状态序列和观测序列长度T=5;
初始概率分布为:
状态转移概率分布为:
观测概率为:
第二个因此隐形马尔科夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定
根据隐马尔科夫模型定义,可以将一个长度为T的观测序列O=(o1, o2, o3,...,oT)的生成过程描述如下:
输入:隐马尔可夫模型λ(A,B,π),观测序列长度T
输出:观测序列O=(o1, o2, o3,...,oT)
再次因此,直接看下图,十分重要↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
隐马尔科夫模型(二)
隐马尔科夫模型有3个基本问题:
(1)概率计算问题,改定模型λ(A,B,π)和观测序列O=(o1 o2 ... oT) , 计算在模型λ下观测序列概率P(O|λ)。
(2)学习问题,已知观测序列O=(o1 o2 ... oT),估计模型模型λ(A,B,π)参数,使用在该模型下观测序列概率P(O|λ)最大。
(3)预测问题,也成解码问题。已知观测序列O=(o1 o2 ... oT),估计模型模型λ(A,B,π)参数,求对给定观测序列条件概率P(I | O)最大的状态序列。
针对第一个问题的概率计算算法:
计算观测序列概率P(O|λ)的前向与后向算法:(以下只介绍前向算法)
首先定义前向概率:
给隐马尔科夫模型λ,定义到时刻t部分观测序列为(o1 o2 ... oT),且状态为qt的概率为前向概率,记作:
具体算法如下:
还是举个栗子能说明问题:
隐马尔科夫模型(三)
隐马尔科夫模型有3个基本问题:
(1)概率计算问题,改定模型λ(A,B,π)和观测序列O=(o1 o2 ... oT) , 计算在模型λ下观测序列概率P(O|λ)。
(2)学习问题,已知观测序列O=(o1 o2 ... oT),估计模型模型λ(A,B,π)参数,使在该模型下观测序列概率P(O|λ)最大。
(3)预测问题,也成解码问题。已知观测序列O=(o1 o2 ... oT),估计模型模型λ(A,B,π)参数,求对给定观测序列条件概率P(I | O)最大的状态序列。
针对第二个问题的学习算法:
学习问题,已知观测序列O=(o1 o2 ... oT),估计模型模型λ(A,B,π)参数,使在该模型下观测序列概率P(O|λ)最大。可以解释为,用了什么样的模型才能最大概率的得到这样的观测。
隐马尔科夫模型的学习,根据训练数据是包括观测序列和对应的状态序列还是只有观测序列,可以分别由监督学习和非监督学习实现。
1.监督学习算法(观测序列+对应状态)

2.无监督学习算法(观测序列+对应状态)
Baum-Welch算法
隐马尔科夫模型(四)
隐马尔科夫模型有3个基本问题:
(1)概率计算问题,改定模型λ(A,B,π)和观测序列O=(o1 o2 ... oT) , 计算在模型λ下观测序列概率P(O|λ)。
(2)学习问题,已知观测序列O=(o1 o2 ... oT),估计模型模型λ(A,B,π)参数,使用在该模型下观测序列概率P(O|λ)最大。
(3)预测问题,也成解码问题。已知观测序列O=(o1 o2 ... oT),估计模型模型λ(A,B,π)参数,求对给定观测序列条件概率P(I | O)最大的状态序列。
针对第三个问题的预测算法:
(3)预测问题,也成解码问题。已知观测序列O=(o1 o2 ... oT) 和 模型λ(A,B,π)参数,求对给定观测序列条件概率P(I | O)最大的状态序列。即给定观测序列,求最有可能的对应的状态序列。
举个栗子:
即求,目前得到的状态为{红、白、红},因此最有可能的拿球状态为{3, 3, 3}。
具体求解如下: