懂相对论之从弯曲空间的几何开始

1古老的几何学

几何是一门古老的学科，在公元前由几何大师欧几里德创立，至今两千多年威力不减。

欧几里德几何是一个漂亮的公理系统，它只需要设定几条简单的、符合直觉、大家公认、不证自明的命题（称为公理或公设），然后从这几条命题出发，推导证明其它命题，继而推导证明更多命题，如此继续下去，一套数学理论便建立起来了。这就像是建造高楼大厦，“公理”就是水平放在地基第一层的大“砖块”，有了牢靠坚实的基础，其它砖块便能够一层一层叠上去，万丈高楼也就能够平地而起。基底砖块破缺了，或者置放得不平稳，楼房就可能会倒塌。

欧几里德平面几何的公理有五条。他就从这简单的五条公理出发，推演出了所有的平面几何定理，建造出欧氏几何的宏伟大厦。

数学逻辑推理创造的奇迹令人吃惊。不过，当人们反复思考这几条公理时，觉得前面4条显然都是不言自明的，唯有第五条公理比较复杂，听起来不像一个简单而容易被人接受的直觉概念。于是，人们就自然提出疑问：这第五条是公理吗？它是否可以由其它4条公理推导出来？大家的意思就是说，欧氏平面几何的大厦用前面4块“大砖头”可能也就足以支撑了。这第五块砖头，恐怕本来就是放置在另外四块砖头之上的。

欧氏平面几何的第五条公理也称为“平行公理”，可表述为：“过直线外的一点，有且仅有一条平行线。”

一位名叫尼古拉·罗巴切夫斯基（Nikolai Lobachevsky，1792 - 1856）的年轻俄罗斯数学家突发奇想：如果将这条公理稍稍改变一下，也就是说，将大厦下面的某块基石稍微移动一下，会产生什么样的后果呢？比如说改成：“过直线外的一点，至少有两条平行线。”

这一改非同小可，几字之差，生出了与欧氏几何完全不同的另一种几何，人们称之为“非欧几何”或“罗氏几何”。非欧几何的大厦同样拔地而起、稳固牢靠，逻辑上完整而严密，但看起来却有些古怪。

罗氏几何体系得到古怪而不合常理的命题是必然的，因为被罗巴切夫斯基改变之后的第五公设，本身就与人们的日常生活经验不相符合。过平面上直线外的一点，怎么可能作出多条不同的直线与已知直线不相交呢？由此而建造出来的数学逻辑大厦，当然会是个怪物。比如说，罗氏几何导出了如下古怪的命题：同一直线的垂线和斜线不一定相交；不存在矩形，因为四边形不可能四个角都是直角；不存在相似三角形；过不在同一直线上的三点，不一定能作一个圆；一个三角形的三个内角之和小于180度……这种奇怪的“几何大厦”，能有什么用处呢？有人嗤之以鼻，心想，不过是疯子数学家玩的游戏而已！

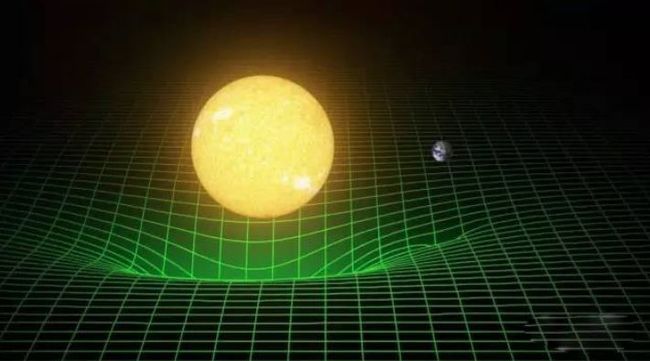
那些嘲笑罗巴切夫斯基的人没有料到，几十年之后，非欧几何在爱因斯坦的广义相对论中找到了用武之地，它正是爱因斯坦广义相对论描述的一种弯曲空间所遵循的几何！

2几何上的无穷小

不过，真正与广义相对论弯曲空间有关的是“黎曼几何”，它比上面所说的非欧几何更进了一步，属于微分几何。

欧几里德之后，笛卡尔发明了解析几何，牛顿和莱布尼茨发明了微积分。两者之结合使得那个时代的数学和物理如虎添翼，面目一新。像罗巴切夫斯基那样使用传统的公理方法来研究几何，显然要输人一筹。欧拉、克莱洛、蒙日以及高斯等人认识到了这一点，创立并发展了微分几何。

微分几何的先行者、法国数学家亚历克西斯·克莱洛（Alexis Clairaut，1713 - 1763）对空间曲线进行了深入研究，第一次研究了空间曲线的曲率和挠率（当时被他称之为双重曲率）。

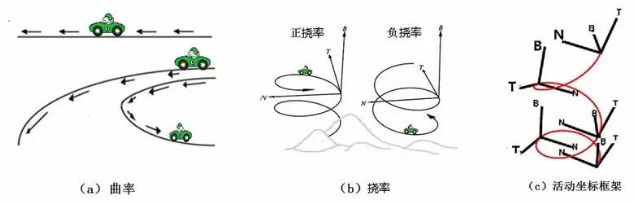
什么是曲线的曲率和挠率？我们从图1a所示的三条平面曲线来认识曲率。图中的三条曲线，就像是三条形状不同的平地上的高速公路。

图1：曲线的曲率和挠率

我们首先需要引进曲线的切线，或称之为“切矢量”的概念。切矢量即为，当曲线上两点无限接近时，它们的连线的极限位置所决定的矢量。图1a所示的公路上标示的箭头，便是在曲线上各个点切矢量的直观图像。而曲率是什么呢？曲率表征曲线的弯曲程度。比如，图1a中最上面一条公路是直线，直线不会拐弯，我们说，它的弯曲程度为0，即曲率等于0。切矢量旋转得越快，曲线的弯曲程度也越大。所以，数学上就把曲率定义为曲线的切矢量对于弧长的旋转速度。

平地上弯弯曲曲的公路可以看作是平面曲线，用“曲率”就可以描述它们。如果公路是修建在山区中，它们一边转弯一边还要盘旋向上或者向下。这时候，汽车驶过的路径便不再是平面曲线，而是空间曲线了。对于山间的公路，如图1b所示，我们除了可以看到其弯曲的程度之外，还能观察到公路往上（或者向下）绕行的快慢。我们将这个描述绕行快慢的几何量叫做“挠率”。

一条空间曲线的曲率和挠率在空间的变化规律完全决定了这条曲线。

从上面对空间曲线的研究，可以看出微分几何的方法比欧氏几何公理式的方法要强有力多了。与曲线类似，微分几何也能用以研究曲面，曲率和挠率的概念，也能推广到曲面上，去定义复杂得多的曲率张量。

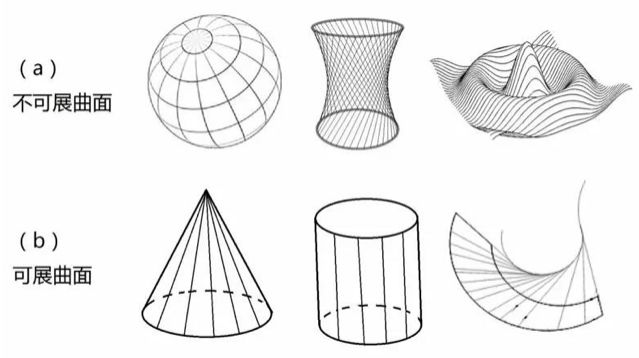
图2：各种曲面

曲面的形状变幻无穷，按照我们感兴趣的性质，可以将其分为两大类：可展曲面和不可展曲面。初看图2a和图2b所画出的曲面，也许你看不出这两类图形有何区别。它们都是从三维空间看到的形状。不管可展还是不可展，看起来不都是“弯曲的”、“不平的”吗？然而，如果你再仔细观察，就会发现，可展曲面的“弯曲”与不可展曲面的“弯曲”有着本质的区别。简单地说，可展曲面在本质上是“平的”，它们可以被展开成一个平面。比如，将图2b所示的锥面，用剪刀剪一条线直到顶点，就可以没有任何皱褶地将它平摊到桌子上。柱面也可以沿着与中心线平行的任何直线剪开，成为一个平面。

但是，图2a所列举的不可展曲面，就不能展开成平面了。那是真正的、本质上的“不平”。一顶做成了近似半个球面的帽子，你无论怎样剪裁它，都无法将其没有皱褶地摊成一个平面。另一方面，你用一张平平的纸，很容易卷成一个圆筒（柱面），或者是做成一顶锥形的帽子，但你无法做出一个球面来。你顶多只能将这张纸剪成许多小纸片，粘成一个近似的球面！

谈到这儿，你大概已经基本明白了“可展”和“不可展”的区别到底是什么。尽管两类曲面在嵌入3维空间之后看起来都是弯曲的，但是，可展曲面的内在本质是“平的”，不可展曲面的内在本质是“不平”。区分这两类曲面“内在本质”的概念叫做“内蕴性”，研究这种性质的几何叫做内蕴几何。

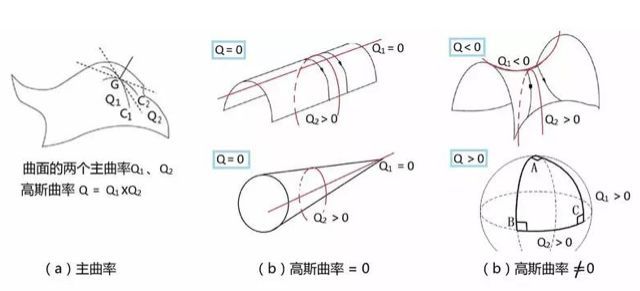
曲面弯曲的内蕴性最早被“数学王子”高斯注意到，后为黎曼所发展，并推广到大于3的n维流形。因而，黎曼几何是一种内蕴几何。换言之，内蕴性指的是曲面（或曲线）不依赖于它在三维空间中嵌入方式的某些性质。也就是说，它是曲面某些内在的、本质的几何属性。高斯用高斯曲率——两个主曲率的乘积，来表征曲面的这种属性（图3a）。如果一个曲面的高斯曲率为0，说明它本质上是平的，是可展曲面，如图3b所示。如果一个曲面的高斯曲率不为0，说明它本质上是不平的，是不可展曲面，如图3c所示。

高斯曲率不为0的情形又有两种。正的高斯曲率对应于球面几何（图3c的下图），负的高斯曲率对应于马鞍面（图3c的上图）。马鞍面上的几何就是前面所介绍的罗巴切夫斯基几何，又被称为双曲几何。

图3：曲面的两个主曲率及高斯曲率

3爬虫的几何

可是，又该如何判定我们所面对的是哪一种几何呢？最简单的办法是测量曲面上一个三角形三个内角之和E=A+B+C。平面几何的E=180o，球面几何E>180o，双曲几何E<180o。

一个观察者在自己生活的物理空间中所能够观察和测量到的几何性质，就是这个空间的内蕴性质。比如说，球面的内蕴性质，就是生活在球面上的2维爬虫感受到的几何性质。我们人类当然是3维的生物，不是什么2维爬虫。但是，因为我们的地球很大，我们的3维尺寸比起地球来说是很小的。因此，我们可以将自己设想为某种2维生物。比如，我们在地球上测量一个大三角形，就如图3b下中的球面三角形ABC，测地员将会发现，这个三角形的三个内角都是90度，因此，内角和E=270o，大于180度。

图3b下所显示的是一个规则球面，它的空间弯曲程度到处都是一样的，但一般来说，空间的弯曲程度不一定处处相同，数学家们用“平

行移动”的概念来研究空间的弯曲程度。

什么是平行移动？简单地说，就是将一个矢量平行于自身的方向沿着空间里的一条曲线移动。像汽车上的陀螺仪那样，汽车沿公路运动时，陀螺仪总是平行于自己原来的指向。

在物理上，让大家更感兴趣的问题是：一个矢量平行移动一圈后再回到原来出发点的时候是否会有所改变？比如说，跟着汽车转了一圈的陀螺仪，指的方向是否还和原来出发时的方向一样？也许你不加思索就会给出答案：当然没有什么改变。但这是因为你习惯了用欧氏空间的直角坐标系来思考问题，从而轻易得出这个结论。如果我们假设地面是一个欧几里德平面，陀螺仪平行移动回到原处时，方向的确不会改变。但是，每个人都知道，地球是一个球体，所以我们实际上是生活在一个球面上。那么，如果从球面（或者别的曲面）的角度来研究这个问题，又会得出什么样的结论呢？

所谓“平行移动”的意思是说，在移动矢量的时候，尽可能保持矢量方向相对于自身没有旋转。好比一个女孩平行地前进、后退、左右移动，只要她的身体没有扭动，就叫平行移动。这样，当她移动一周回到出发点的时候，她认为她应该和原来出发时面对着同样的方向。如果她是在平面上移动的话，她的这个想法是正确的。但是，假如她是在球面上移动的话，她将发现自己面朝的方向可能不一样了！出发时她的脸朝左，回来时却是脸朝前，如图4b。

假如将女孩面对的方向用一个箭头（矢量）来表示。图4a所示的是一个矢量在莫比乌斯带上的平行移动，当矢量从位置1出发，沿着数字1、2、3……一直移动到10，也就是回到原来的出发位置时，得到的矢量和原来的反向。图4b中所示是球面上的平行移动，当矢量从位置1出发，沿着数字1、2、3……一直移动到7，也就是回到原来的出发位置时，得到的矢量和原来的矢量垂直。

图4：（a）莫比乌斯带上的平行移动（b）球面上的平行移动

上面的两个例子说明，矢量在曲面上平行移动一周之后，不一定还能保持原来的方向，可能与出发时有所差别。这个差别正好与曲面的高斯曲率有关系，反映了曲面内在的弯曲程度。

4阿扁的世界

下面，我们研究锥面上的平行移动，看看锥面与“真正的平面”有何不同。让我们想象有一个极小极扁的平面生物“阿扁”，生活在一张平坦的纸上，如图5a。阿扁使用直角坐标系对他的平坦世界进行观察和测量。他感受到的几何，是标准的欧几里德几何：三角形的三个内角之和等于180度；过不在同一直线上的三点，可以作一个圆；直角三角形的两条直角边的长度的平方和等于斜边长的平方……

阿扁学过微积分，还会计算许多图形的面积。阿扁经常在他的平坦世界中驾车旅行，绕行一圈回来之后，他车上的陀螺仪方向总是与原来方向相同，如图5a所示的那样。

有一天，来了一个3维世界的小生物“阿三”。阿三看中了阿扁生活的这张纸，并且灵感突发，把这张纸剪去了一个角。比如说，像图5b中图所画的情形，剪去了一个45度的角，然后将剩余图形的两条剪缝黏在一块儿，做成了一个图5c所示的锥面。阿扁是个2维小爬虫，他看不见阿三，也感觉不到阿三的存在，更不可能知道阿三对他的世界干了些什么。

不过，生活在纸上的阿扁并没有立即感到他的世界有什么变化。照样是欧氏几何，他画的直角坐标轴仍然在那儿。当他拿着他的（平面）陀螺仪，沿着他的小圆圈（如图5b中的C1那样）旅行，进而回到原来出发点的时候，陀螺仪的指向和原来一样。这说明，矢量平行移动的规律好像没有任何改变。

图5：阿扁的世界

阿扁的技术越来越高，胆子越来越大，旅游路线也走得越来越远。他逐渐发现了一些问题。比如说，当他沿着图5b中所示的C2那样的曲线走一圈回到原出发点时，他的陀螺仪的指向和出发时有了一个45度的角度差。这个新发现令阿扁既激动又困惑。于是，他进行了更多的带陀螺仪绕圈实验，绕了好多个不同的圈，终于总结出了一个规律：他生活的世界中，在右图中所标记的点O附近，是一个特殊的区域，只要他移动的闭曲线中包含了这个区域，陀螺仪的指向就总是和原来出发时的方向相差45度左右。如果行走的圈没有包括这个点的话，便不会使陀螺仪的方向发生任何改变。当时的阿扁，技术还不够精确，还没有搞清楚这个区域是多大，况且，他也有点害怕那块神秘兮兮的地方，不敢在那儿逗留过久，作太多的探索，以防遭遇生命危险。

阿扁喜欢读书学习新知识，他从一本数学书中了解到，如果陀螺仪走一圈方向改变的话，说明你所在的空间是弯曲的。因此，通过对多次实验结果的总结归纳，阿扁提出一个假设：他所在的世界基本是平坦的，除了那块该死的区域之外！

再回到我们的世界来看待球面几何。陀螺仪走一圈后方向改变的值，叫做平行移动一周后产生的角度亏损，可用θ表示。角度亏损与空间的高斯曲率有关，一个标准球面上的高斯曲率处处相等。因此，如果有某种生活在球面上的扁平生物的话，他沿任何曲线绕行一圈后，陀螺仪方向都会有变化，而且，角度亏损θ是不固定的，它与绕行回路所包围的球面面积A成正比，其比例系数对球面而言是一个定植，就等于曲面的高斯曲率α。角度亏损θ = α*A。

如果研究对象不是标准的球面，而是一般的2维曲面，上述“角度亏损θ正比于区域面积A”的结论在大范围内不能成立，但在2维曲面某个给定的P点附近，当绕行的回路趋近于无限小的时候仍然成立。也就是说：无限小的角度亏损dθ将正比于无限小的区域面积dA：dθ = α*dA。这时的α= dθ/dA，便是曲面上这一点的曲率。

阿扁也想通了这些道理，明白他的世界不是球面，而大多数地方都是平面，只有一点不对，那一点附近的空间是弯曲的。

阿扁将上面有关曲面曲率与无限小平行移动角度亏损的关系（α= dθ/dA）用到锥面。因为锥面是一个可展曲面。它所有地方的几何都与平面上的欧几里德几何一样，除了那个顶点以外。也就是说，锥面上每个点的曲率都等于0，但顶点是一个曲率等于无穷大的奇点。

有了这些数学知识，阿扁恍然大悟：原来我生活的世界是一个锥面！

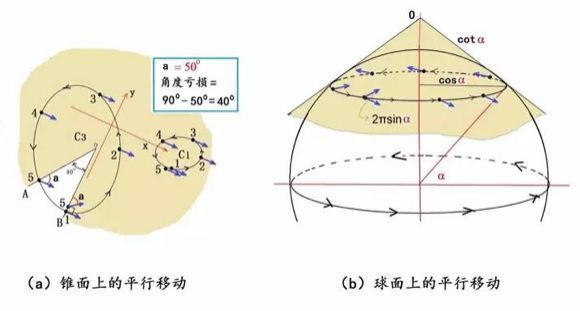
图6：锥面和球面上的平行移动

人类是3维空间的生物，我们的世界是3维的。就像前面所描述的“阿三”，当然要比那个可怜的平面生物“阿扁”高明多了。阿扁反复测量了许多次，用他的2维扁平脑袋，作了极端困难的“抽象”，才弄明白了他的锥面世界！而我们在3维世界中看2维就能看得非常清楚了：锥面是一个可展曲面，或者说，本来就是由阿三将一张平面的“纸”剪去了一个角而粘成的。因此，我们瞄一眼就知道，阿扁的锥面世界处处都是平坦的，除了那一个顶点O之外。

在锥面上作平行移动时，为什么当移动路径包括了顶点O的时候就会有角度亏损呢？从我们的3维世界更容易理解这个问题。在图6a中，我们将锥面从顶点剪开后重新展开还原成一个平面图形。这个“剪去一角的平面图形”与整个欧几里德平面的区别在于，图中的A和B是锥面上的同一点，因此，直线OA和OB需要被理解为是同一条线。这样，我们就明白了角度亏损的来源。

∑编辑 | Gemini

来源 | 科学网博主文/张天蓉 

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域

经采用我们将奉上稿酬。

投稿邮箱：[email protected]