时间序列分析之相关性

目录

方差 (Variance)

相关系数 （Correlation）

自相关/序列相关 (Autocorrelation or Serial Correlation)

两种时间序列的相关性

---

方差 (Variance)

设随机变量X的均值 E(X) = m，则描述 X 的取值和它的均值 m 之间的偏差程度大小的数字特征就是方差。

但是不能直接用 E(X - m) 来表示方差，因为 E(X - m) = E(X) - m = 0，X 的正负偏离彼此抵消了。所以先将 X - m 平方后再取其均值，也就是偏差的平方

协方差 (Covariance)

根据方差的定义，Var(X) = E[(X - E(X)) × (X - E(X))]，将其中的一个 X 和 E(X) 用另一个 变量Y表示，Var(X) = E[(X - E(X)) × (X - E(X))]，也就是

为了方便表示，

关于协方差有几个重要的定理：

1. 如果 X, Y相互独立，则 Cov(X, Y) = 0

2. ，当且仅当 X,Y 之间有严格线性关系的时候等号成立。

 

相关系数 （Correlation）

相关系数也就是经常提到的皮尔逊（Pearson）相关系数，常用 Corr 或者 r 来表示相关系数。相关系数可以看作是标准尺度下的协方差

相关系数有有个定理：

1. 如果X, Y相互独立，则 Corr(X, Y) = 0

2. ，当且仅当 X,Y 之间有严格线性关系时候，等号成立。

 

自相关/序列相关 (Autocorrelation or Serial Correlation)

模型随机项之间存在相关性称为自相关或者序列相关。

对于模型

随机项存在序列相关是：，最简单的一阶序列相关也就是

下面用 python 中的statsmodel 模块来分析一下时间序列的自相关性：

生成一段高斯白噪声，然后画出它的ACF (AutoCorrelation Function)和PACF(Partial AutoCorrelation Function)。

补充一点关于 ACF 和 PACF的作用：根据ACF和PACF可以直观看出序列的自相关性，并且还可以作为一种判断序列是否平稳的手段，从而选择合适的模型来拟合数据。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import gridspec
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

def ts_plot():
    fig = plt.figure()
    gs = gridspec.GridSpec(2,2)

    data = np.random.normal(size=1000)

    ax_ts = fig.add_subplot(gs[0, 0:2])
    ax_acf = fig.add_subplot(gs[1, 0])
    ax_pacf = fig.add_subplot(gs[1, 1])

    ax_ts.plot(range(len(data)), data)
    plot_acf(data, ax=ax_acf, lags=30)
    plot_pacf(data, ax=ax_pacf, lags=30)

    plt.show()

可以看出白噪声过程的ACF和PACF中并没有什么明显的相关性。

下面模拟一段 AR(1) 的过程。

def ts_plot():
    fig = plt.figure()
    gs = gridspec.GridSpec(2,2)
    u = np.random.normal(size=1000)
    data = u
    a = 0.6
    for t in range(1000):
        data[t] = a * data[t-1] + u[t]
    ax_ts = fig.add_subplot(gs[0, 0:2])
    ax_acf = fig.add_subplot(gs[1, 0])
    ax_pacf = fig.add_subplot(gs[1, 1])

    ax_ts.plot(range(len(data)), data)
    plot_acf(data, ax=ax_acf, lags=30)
    plot_pacf(data, ax=ax_pacf, lags=30)

    ax_ts.set_title('AR(1)')
    plt.show()

ACF拖尾，PACF一阶截尾 ，所以很明显是一个AR(1)过程。

 

两种时间序列的相关性

时间序列的自相关性可以理解为时间序列自己与自己（不同滞后项）之间的相关性，有时需要研究不同时间序列之间的相关性，例如配对交易时选择具有相似走势的股票对。

选出相同板块的几只股票，相同板块受到的政策市场等影响类似，所以它们的价格走势的相关性也应该比较高。通过 tushare 爬取这几只股票的收盘价数据：

def calSim():
    symbols = ['600831', '603000', '603888', '300431', '002238', '600037']
    used_cols = ['code', 'close']
    df = ts.get_hists(symbols, start='2018-12-01', end='2018-12-30')
    df = df[used_cols]
    df_Close = pd.DataFrame()
    
    pos = [321,322,323,324,325,326,327,328]
    i = 0
    fig = plt.figure()
    for symbol in symbols:
        ax = fig.add_subplot(pos[i])
        ax.plot(range(len(df_Close[symbol])), df_Close[symbol])
        ax.set_title(symbol)
        i += 1
    plt.tight_layout()    # change the distance of subplots
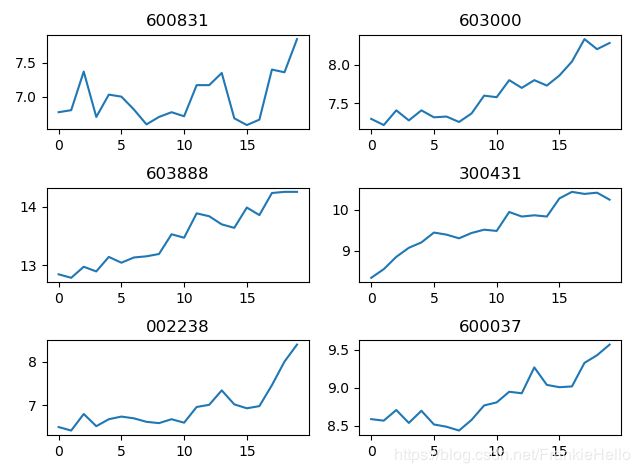
    plt.show()

 从图中可以看出60300和603888以及603000和60037这两组之间的相似性比较高，而600831与其它股票的差别较大。下面通过画出它们之间的相关图来量化一下这种相关性。

   for symbol in symbols:
        value = df.loc[df['code'] == symbol, 'close'].values
        df_Close[symbol] = value
    print(df_Close)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    sns.heatmap(df_Close.corr(), ax=ax, annot=True)
    plt.show()

 结果跟我们观察的一样，看出60300和603888以及603000和60037这两组之间的相关性高，而600831与其他的之间的相关性较低。其中两两之间的相关性矩阵就是通过 df.corr() 得到的，df.corr() 函数默认计算相关系数就是通过皮尔逊相关系数计算得到的。