树状数组( 单点修改/区间修改+区间求和+一维/二维）

树状数组(Binary Indexed Tree(BIT), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值。

首先照例附上树状数组的百度百科解释。实际上，经过“简单修改”可以做到区间修改与区间求和。树状数组，在你写线段树区间求和写的吐血的时候，是个不错的选择。

一维+单点修改+查询

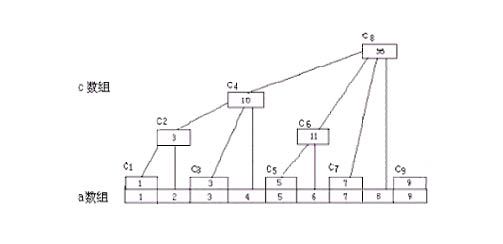
这张图片在很多树状数组的讲解中都有出现过。明确，c数组是我们的树状数组，a数组是我们的基础数组。我们所有的操作都是基于c数组上的，但是事实上题目所给我们的只有a数组。

区间求和操作，实际上可以转换为维护数组前缀和的操作。由树状数组的标准解释来说，树状数组天生就是为了维护数组前缀和的。

规定add(x,addtag)操作为将a[x]加上addtag,get_sum(x)操作为求a[1]-a[x]的和。

先从get_sum()操作讲起，从图中我们可以很简单的得到，c[]可以由多个c[]及a[]得到。例如c[8]=c[4]+c[6]+c[7]+a[8]。如果我们将c[4],c[6],c[7]，均表示为多个c[]及a[]的形式，最终我们会发现，我们得到c[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8].

所以说get_sum(x)操作只需要输出c[x]吗？显然不是。

我们换一个例子。
c[7]=a[7]，而get_sum(7)显然不等于a[7]。经过观察发现，get_sum(7)=c[7]+c[6]+c[4]。我们仔细观察这张图，会发现一些无法用言语描述的奇妙规律。（当然你也很可能会描述）只要表示出这些规律我们就完成了任务，于是我们把这些数字写成二进制。

get_sum(111) = c[111] + c[110] + c[100];

看出什么了吗？为了更好的表述这个规律，我们应用lowbit（x）表示清除二进制下x 除了最低位的1 之外，所有高位的1.

lowbit函数表示如下

int lowbit(int x)
{
    return x&(-x);
}

那么每一个get_sum(x)都是从低位开始，依次清空1，知道清空到没有1 为止。
代码如下：

int get_sum(int x)
{
    int ans=0;
    while(x)
    {
        ans+=c[x];
        x-=lowbit(x);
    }
    return ans;
}

get_sum()操作到此结束 :)

get_sum()操作可以说是从高往低的，很简单可以想到，add()操作即是相反的get_sum()操作，是从低往高的。我们将每一个单点的 delta 加入它所影响的c[]中（即 c[]包括该点值），到n为止。
代码如下：

void add(int add,int addtag)
{
    while(x<=n)
    {
        c[x]+=addtag;
        x+=lowbit(x);
    }
}

树状数组除却求和外，还可以实现最大值与最小值的维护，在此略过不提。

一维+区间修改+查询

我们总是会遇到所谓的区间修改的题目。在这种时候将整个区间中的每个点分别进行处理显得极为愚蠢，于是我们通过引入新的树状数组来解决这个问题。

我们用数组delta[]进行辅助,delta[i]表示为从i-n,每个点都总共增加了delta[i].
于是对于某个区间[l,r]进行+1的操作，即相当于进行如下两个操作：

delta[l]+1
delta[r+1]-1

确保你理解以上这两个式子是怎么来的后，我们来看这么一段转换。设a[]为原数组，则get_sum(x)分为了两部分，一为a[],一为delta[].

delta[i]对于get_sum(x)的贡献值为delta[i] * (x-i+1)

整理得到

get_sum(x)
=a[1]+a[2]+…+a[x] + segma(delta[i]*(x-i+1))(1<=i<=x)
=segma(a[i])+segma(delta[i])*x-segma(delta[i]*i)(1<=i<=x)

显然这三个大大的segma告诉我们，整个的get_sum（）是可以用树状数组维护的。我们只需要增加segma(delta[i])与segma(delta[i]*i)这两个树状数组，并在求和的时候进行加减乘的运算即可。

二维+区间修改+查询

请确保你在弄清楚以上所有的内容之后，再来看我的胡言乱语，谢谢:)

一个立体图形是由一堆的面堆起来得到的，那么一个二维树状数组，是将一个树状数组的每一个c[]节点，建立成为一个新的树状数组而得到的。

这张图中的c[i]不再是一个节点，而是一个代表了一个树状数组c[]，我们所有的操作都是在更改某个树状数组c[]的第二维，即，c[][]的值。

void add(int x,int y,int d,int c[MAXN][MAXN])
{
    for(int i=x;i<=n;i+=lowbit(i))
        for(int j=y;j<=n;j+=lowbit(j))
            c[i][j]=c[i][j]+d;
}

int get_sum(int x1,int y1,int c[MAXN][MAXN])
{
    int ans=0;
    for(int i=x1;i>0;i-=lowbit(i))
        for(int j=y1;j>0;j-=lowbit(j))
            ans=ans+c[i][j];
    return ans;
}

在这种思想上，二维的区间修改也变得简单，原先我们只需要维护x一个变化量，如今我们需要维护x,y两个变化量，只需要将原谅的一个树状数组，拆成两个部分就好了。

void add_all(int x,int y,int addtag)
{
    if(!x || !y)return;

    add(1,1,addtag,c_in_xy);
    add(x+1,1,-addtag,c_in_xy);
    add(1,y+1,-addtag,c_in_xy);
    add(x+1,y+1,addtag,c_in_xy);

    add(x+1,y+1,x*y*addtag,c_in_);

    add(x+1,1,x*addtag,c_in_y);
    add(x+1,y+1,-x*addtag,c_in_y);

    add(1,y+1,y*addtag,c_in_x);
    add(x+1,y+1,-y*addtag,c_in_x);
}

int get_sum_all(int x,int y)
{
    return get_sum(x,y,c_in_xy)*x*y + get_sum(x,y,c_in_) + get_sum(x,y,c_in_y)*y +get_sum(x,y,c_in_x)*x;
}

错误是我的，请让我吃掉他们:(