Adaptive Deconvolutional Networks for Mid and High Level Feature Learning（阅读）

Adaptive Deconvolutional Networks for Mid and High Level Feature Learning（阅读）

Matthew D. Zeiler, Graham W. Taylor and Rob Fergus
Dept. of Computer Science, Courant Institute, New York University
fzeiler,gwtaylor,[email protected]

• Adaptive Deconvolutional Networks for Mid and High Level Feature Learning（阅读）
  
  • Abstract
  • Introduction
  • 1.1 Related Work
  • 2. Approach
    
    • Deconvolution
    • Pooling
    • Multiple Layers
    • 2.1 Inference
    • 2.2.Learning
  • 3.Application to object recognition
  • 4.Experiments
    
    • 4.1.Model visualization
    • 4.2.Evaluation on Caltech-101
    • 4.3.Evaluation on Caltech-256
    • 4.4.Transfer learning
    • 4.5.Classification and reconstruction relationship
    • 4.6.Analysis of switch settings
  • 5.Discussion
  • References

Abstract

我们提出一种分级（hierarchical）模型，该模型通过稀疏卷积编码层和最大池化层的交替学习到图片的分解（decompositions）。当模型在原始图像上训练时，它的这些层会抓取图像的多种信息：低级边缘(low-level edges), 中级边缘连接(mid-level edge junctions),目标的高级部分和完整的目标(objects high-level object parts and complete objects).我们以一种新的推断方案来建立模型，该方案确保每一层重构输入而不是只有向下直接输出，因此与当前的分层方法一样。这样使得学习多层特征成为可能，并且我们展示了模型的4层特征，模型基于Caltech-101和256 数据集训练。当结合一个标准的分类器，模型的特征提取表现超过SIFT，以及其他特征学习方法。

Introduction

对于视觉多任务来说，关键的问题是发现好的图像表示。比如说，本地图像描述子的出现，如SIFT、HOG在匹配和目标识别中已经取得了巨大的进步。有趣的是，许多成功的representations是非常相似的，关键是围绕边缘梯度的计算，其次是一些直方图和池的操作。虽然捕获低级图像结构是有效的，但是有难度的是找到适当的中高级表示(representations)，即角，连接点和对象部分，这些对于理解图像很重要。

本文中提出一种学习图像representations的方法，它以无监督的方式从低级边缘到高级对象部分的所有尺度中提取结构。在建立我们的模型时，我们提出了与特征层次相关的两个基本问题的新颖的解决方案。 第一个与不变性(invariance)有关：边缘仅在方向和尺度上有所不同，较大尺度的结构更为可变。 例如，试图明确记录所有可能形状的T形接合点或拐角，都会导致一个在原始数量上呈指数形式的模型。 因此，不变性对建模中高层结构至关重要。

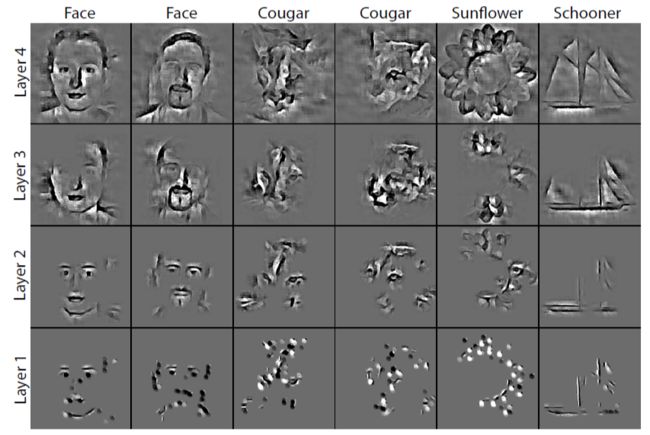
图1.从上往下由自适应反卷积网络方法得到图像的逐步分解。 每列对应于相同模型下的不同输入图像。 第1行显示投影到图像空间中的第4层特征图的单次激活。 在上述层次的激活条件下，我们还分别在第3层，第2层和第1层中分别采用5,25和125个活动特征的子集，并在图像空间（第2-4行）中进行可视化。 这些激活揭示了我们模型所学到的中级和高级原语(peimitives)。 在实践中，还有更多的激活，这些激活使得完整的集合可从每个层重构整个图像。

第二个问题涉及到在分级(hirarchical)模型中使用的逐层训练方法，如深度置信网络DBN[6,11]和卷积稀疏编码[3,8,20]。缺少一种对输入来说高效训练所有层的方法，这些模型从下到上贪婪地训练，使用上一层的输出作为下一层的输入。该范例的主要缺点是图像像素在第一层之后被丢弃，因此模型的较高层与输入端之间的联系逐渐减弱。这对几层以上的模型来说是脆弱和不切实际的。

我们解决这两个问题的方法是引进一组为每个图像计算的潜在门(switches)变量，使模型的滤波器(filters)在本地适应观测数据。因此，相对简单的模型可以捕捉图像结构的广泛变化。这些门(switches)还提供了直接到输入的路径，即使处在模型中的高层，也可以使每个层相对于图像进行训练，而不是先前层的输出。正如我们所展示的，这使得学习更加强大。此外，门(switches)可以使用有效的训练方法，使我们能够在数千个图像上学习具有多个层次和数百个特征图的模型。

1.1 Related Work

卷积网络（ConvNets）[10]，像我们的方法一样，通过学习滤波器生成潜在的特征图。但是，他们自下而上的处理图像并有区别的(discriminatively)和纯监督的训练，而我们的做法是自上而下（生成）和无监督的。预测稀疏分解（PSD）[7]在ConvNets中添加了一个可以无监督训练的稀疏编码组件。与我们的模型相反的是，每层只重构下面的层。如[12]中可以通过记录用于重构变换的参数来引入额外的移位不变性(additional shift invariance)。

深度置信网络共享这一限制（DBNs）[6,11]，其由限制玻尔兹曼机器层(RBMs)组成。每个RBM层以其输入为条件，具有不直接执行解释的因子表示。此外，训练相对较慢。

最接近我们的方法是基于卷积稀疏编码的方法[3,8,20]。像PSD和DBN一样，每层只尝试重构下层的输出。此外，它们手动地在不同层的特征图之间施加稀疏连接，从而限制了所学习的表示的复杂性。相反，我们的模型具有连接性层，这让我们学习更复杂的结构。另外的差异包括：缺乏池化层[20]和无效率的推理方案[3,20]，这些方法没有扩展。

我们的模型表现的是整张图像的分解，借鉴了Zhu 和 Mumford[22] 和 Tu和 Zhu[16]的要义。 这与其他分层模型不同,如Fidler和Leonardis [4]和Zhu et al.[21]，仅在每个级别而不是所有像素建立稳定的图像结构子集。 我们的方法的另一个关键方面是从自然图像学习分解/分量。 其他的分层模型，如Serre等人的HMax [13,15]和
郭等[5]在每层使用手工制作的功能。

2. Approach

我们的模型产生了一个完整的可用作标准物体(object)分类器输入的图像表示。 与许多图像表示不同，我们从自然图像中学到，并且给定一个新的图像，需要推断计算。 该模型使用卷积稀疏编码（deconvolution [20]）和max-pooling的多个交替层以分层方式分解图像。每个反卷积层都试图在一组完整的特征图上的稀疏约束条件下直接最小化输入图像的重构误差。

l l 层的代价函数 Cl(y) C l ( y ) 由两部分构成：
(i)概率项(置信度)：使输入 y y 的重构项 y^l y ^ l 接近原始输入图 y y
(ii)正则项：惩罚重构图像 y^l y ^ l 所依赖的二维特征图 zk,l z k , l 的 l1 l 1 范数
两项的相关权值由 λl λ l 控制:

Cl(y)=λl2∥y^l−y∥22+∑k=1Kl|zk,l|1(1) C l ( y ) = λ l 2 ‖ y ^ l − y ‖ 2 2 + ∑ k = 1 K l | z k , l | 1 ( 1 )

不同与已有的方法[3,8,20],我们的卷积稀疏编码层尝试直接最小化输入图像的重构误差，而不是下层的输出。

Deconvolution

考虑模型的第一层，见图2(a).重构值 y^1 y ^ 1 (有 c c 个颜色通道)由2D特征图 zk,1 z k , 1 与卷积核 fck,1 f k , 1 c 卷积并求和得到:

y^c1=∑k=1K1zk,1∗fck,1(2) y ^ 1 c = ∑ k = 1 K 1 z k , 1 ∗ f k , 1 c ( 2 )

∗ ∗ 是2D卷积操作。卷积核 f f 是模型的参数共享于所有图像。特征图 z z 每张图像的隐藏变量是独特的。从 K1>1 K 1 > 1 ，模型是over-complete，但是公式(1)中的正则项确保了有唯一解。我们的推断方案旨在找出最优的 z1 z 1 和用于在节2.1 和 2.2中评估 f1 f 1 的最相关的学习方法。为简洁表达，我们将层 l l 的卷积核求和操作变成一个卷积矩阵 Fl F l ，将多个2D特征图 zk,l z k , l 转换成一个 zl z l 向量:

y^1=F1z1(3) y ^ 1 = F 1 z 1 ( 3 )

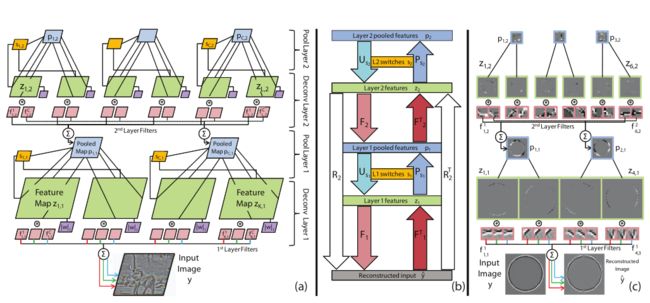
图2.（a）：其中两层的可视化。每层由deconvolution和max-pooling组成。deconvolution层是一种卷积形式的稀疏编码，它将输入图像 y y 分解为特征图 z1 z 1 （绿色）和已学习的滤波器 f1 f 1 （红色），用于卷积并求和以重构 y y 。滤波器具有 c c 个平面，每个平面用于重构输入图像的不同通道。每个 z z map都受到 l1 l 1 形式的稀疏项（紫色）惩罚的约束。max-pooling层在特征图内和特征图之间，能减少特征的大小和数量以得到特征图 p p （蓝色）。每个pooling区域中最大值的位置记录在 s s （黄色）中。第二个deconvolution/pooling层与第一个的概念相同，但现在只有两个输入通道而不是三个输入通道。实际上，我们每层有多个特征图，总共有4层。（b）：第2层模型中推理操作的框图。有关说明，请参见第2.1节。（c）：使用（对比度归一化）圆的单输入图像的训练实例模型在左侧。switches和稀疏项未展示。注意稀疏特征图（绿色）和池化操作的效果（蓝色）。由于输入是灰度图，所以第一层滤波器的平面是相同的。

上图所示的过程
(i)reconstruction(从feature map z2 z 2 重构回imput image)过程：

z2−→−−−⨂F2p1−→−−−Usz1−→−−−⨂F1x^2 z 2 → ⨂ F 2 p 1 → U s z 1 → ⨂ F 1 x ^ 2

(ii)prejection(把error信号回传到 l l 层)的过程：

x^2−→−−−⨂F1Tz1−→−−−Ps1p1−→−−−⨂F2Tz2 x ^ 2 → ⨂ F 1 T z 1 → P s 1 p 1 → ⨂ F 2 T z 2

图3.使用大小为2×2×2的邻域的3D最大池的示例，如颜色所示。池化操作 P P 被应用于特征图 z z ，得到池化特征图 p p 并用 s s 记录最大值(与符号无关)的位置。给定 p p 和对应的 s s ，我们还可以得到 一个反池化结果 U U ，它将池化值插入到特征图中 s s 记录的位置，其余的位置设置为零。

Pooling

在每个deconvolution层的顶部，对特征图 z z 进行3D最大池化。这允许上层的特征图以比当前层更大的尺度来捕获结构。 池化是三维的，因为它在空间上（每个2D z z map内）以及相邻maps之间都发生，如图3所示。在里面 z z 的每个邻域都记录最大值（不论符号）的值和位置。池化的map p p 保留最大值，而switches记录位置。

图3所示的pooling和unpooling过程：
从feature maps z z 中pool出绝对值最大的元素， p p 记录它的值， s s 记录它的位置， s s 是一个三元组 (x,y,k) ( x , y , k ) , (x,y) ( x , y ) 为map内的坐标， k k 为层数。坐标方式如下图。

unpooling:将上述元素按照 s s 的位置填入，其余位置置零。

模型在特征图 z z 上使用两种不同形式的池化操作。首先，如图3所示。将switches视为输出： [p,s]=P(z) [ p , s ] = P ( z ) 。其次，将switches作为输入，它们指定 z z 中的哪些元素被复制到 p p 中。如果s是固定的，那么这是一个可以写为 p=Psz p = P s z 的线性运算，其中 Ps P s 是由 s s 设置的二元选择矩阵。

相应的unpooling操作，如图3所示，将元素放在 p p 中，并将它们放在 z z 指定的位置，其余元素设置为零： z^=Usp z ^ = U s p 。请注意，这也是固定 s s 的线性运算则， Us=PTs U s = P s T 。

Multiple Layers

模型较高层的架构保持不变，但是特征图 Kl K l 的数量可能会有所不同。在每层，我们通过下层的filters和switches重构输入。我们定义一个重构算子 Rl R l ，其从层 l l 获取特征图 zl z l 并且交替地卷积 (F) ( F ) 和unpool (US) ( U S ) 得到输入图像:

y^l=F1US1F2US2...Flzl=Rlzl(4) y ^ l = F 1 U S 1 F 2 U S 2 . . . F l z l = R l z l ( 4 )

注意，重构 y^l y ^ l 取决于当前层的特征图 zl z l 而不是下面那些(换句话说，当我们向下映射到图像，我们不会在任何中间层的重构体 z^l−1,...,z^1 z ^ l − 1 , . . . , z ^ 1 上施加稀疏约束)。然而，这些重构算子 Rl R l 仅取决于中间层池化时的switches (Sl−1...S1) ( S l − 1 . . . S 1 ) 而switches由池化操作 (Usl−1...US1) ( U s l − 1 . . . U S 1 ) 决定。switches通过以前迭代的值 zl−1...z1 z l − 1 . . . z 1 配置。

我们也定义一个投影(projection)算子 RTl R l T ,该投影算子在输入端接收一个信号并将其投射回到层 l l 的特征图，对于给定先前确定的switches s1,...,sl−1 s 1 , . . . , s l − 1 有:

RTl=FTlPsl−1FTl−1Psl−2...PslFT1(5) R l T = F l T P s l − 1 F l − 1 T P s l − 2 . . . P s l F 1 T ( 5 )

我们的模型的关键特性是给定的switches，重构算子 Rl R l 和投影算子 RTl R l T 都是线性的，因此即使在多层模型中也可以容易地计算梯度，从而推断学习是简单的。图2(a)说明了我们的模型中的两个deconvolution层和池化层。图2(b)显示了重构和投影运算如何由滤波，池化和反池化操作组成。

2.1 Inference

对给定层 l l ,，给定输入图像 y y 和滤波器 f f ，推断涉及找到使得特征图 zl z l 最小化的 Cl(y) C l ( y ) 。对于每一层，我们需要解决一个大的 l1 l 1 卷积稀疏编码问题，我们调整了Beck和Teboulle的ISTA方案[1]。它使用gradient和shrinkage的迭代框架。

Gradient step:
计算方程(1)中重构项对 zl z l 方向的梯度 gl g l ：
∂Cl∂zl=gl=RTl(Rlzl−y)=RlTel ∂ C l ∂ z l = g l = R l T ( R l z l − y ) = R l T e l 。

为了计算梯度，我们使用特征图 z1 z 1 ，并且使用下层的滤波器和switches配置来重构输入 y^=Rlzl−y y ^ = R l z l − y 。然后计算重构误差 y^−y y ^ − y 。然后使用 RTl R l T 将其传播回网络，其交替地滤波( FT F T )和池化( PS P S )到层 l l ，产生梯度 gl g l 。该过程的可视化见图2(中部)两层模型。

一旦我们得到梯度，我们就可以更新 zl z l ：

zl=zl−λlβl∂Cl∂zl=zl−λlβlgl(6) z l = z l − λ l β l ∂ C l ∂ z l = z l − λ l β l g l ( 6 )

βl β l 指梯度步长

Shrinkage step：
梯度步骤之后，我们对每个元素执行shrinkage操作，将 zl z l 中小元素置0，以增加其稀疏度。

zl=max(|zl|−βl,0)sign(zl)(7) z l = m a x ( | z l | − β l , 0 ) s i g n ( z l ) ( 7 )

Pooling/unpooling:
然后通过一个pooling操作(这是图3中显示的pooling形式，它将switches作为输出。而在投影算子 RT R T 中它作为输入。) [pl,sl]=P(zl) [ p l , s l ] = P ( z l ) 更新当前层的switches sl s l ,随后紧接一个unpooling操作 zl=USlpl z l = U S l p l 。这包含2个功能：(i)当在顶部构建额外层时确保通过pooling操作能精确地重构输入图像。(ii)它会更新switches以反映功能图的更新。 一旦推理已经收敛，switches将被确定/固定，为训练上层准备。因此，推断的次要目标是确定当前层中的最佳switches配置。

Overall iteration:
单次ISTA迭代包含以上三个步骤：梯度，shrinkage以及pooling/unpooling。在推断期间，对每层的每个图像执行10次ISTA迭代。

重构 R R 和传播 RT R T 操作都非常快，只是由卷积，求和，pooling和unpooling操作组成，所有这些都适用于并行化。 这使得有可能有效地解决方程式1中的系统，即使是大量over-complete层，其中 zl z l 可以长达 105 10 5 。

请注意，虽然梯度步长是线性的，但整个模型并不是。 非线性来自两个部分: (i)由方程7中的shrinkage收缩等式引起的稀疏性。(ii)switches s s 的配置，它改变 R1 R 1 内的pooling/unpooling。

2.2.Learning

学习的目标是训练出所有图片 Y=y1,...yi,...,yN Y = y 1 , . . . y i , . . . , y N 共享的滤波器 f f . 对于给定层 l l ,我们执行计算 zil z l i .利用方程1中Cost Function对 fl f l 的偏导并设置为0，可获得 fl f l 中的线性系统：

∑i=1N(ziTlPisl−1RiTl−)y^il=∑i=1N(ziTlPisl−1RiTl−1)yi(8) ∑ i = 1 N ( z l i T P s l − 1 i R l − i T ) y ^ l i = ∑ i = 1 N ( z l i T P s l − 1 i R l − 1 i T ) y i ( 8 )

y^i y ^ i 是输入利用 fl f l 的当前值得到的重构，我们使用线性共轭梯度求解该系统。通过映射到输入并再次使用 Rl R l 和 RTl R l T 操作来有效地计算左侧的矩阵向量乘积。 求解方程(8)后，我们将 fl f l 归一化为单位长度。用于学习模型的所有层的整体算法在算法1中给出。我们在 zl z l 和 fl f l 中交替小步骤，单次迭代里使用单个ISTA步骤来推导 zl z l 和用两次CG迭代更新 fl f l ，重复十次这样的迭代。推理的过程是相同的，除了第15行的 fl f l 更新不被执行，我们在单个迭代使用10次ISTA推导出 zl z l 。

3.Application to object recognition

该模型是完全无监督的，且必须连接一个分类器用于目标识别。从简洁性和性能方面考虑，我们使用Lazebnik等人提出的空间金字塔分类(SPM).

给定一个新的图像，使用我们的模型执行推理将其分解为多层特征图和switches配置。我们现在描述一种将此分解与SPM分类器结合使用的新颖方法。

虽然滤波器在图像之间共享，但是switches设置不是，因此两个图像的特征图不能直接比较，因为它们使用不同的基 R1 R 1 。例如，在图1中，每个第4层自上而下的分解是从相同的特征图开始的，却给出了完全不同的重构。这显示了模型的两个关键方面：(i)在一个类中或类似的类之间，分解类似的部分共享相似的部分，并且集中在图像的特定区域上; (ii)switches设置的适应性允许模型学习与其他类的复杂交互。然而，这使得直接使用高级特征图对于分类有问题，并且我们提出了不同的方法。

图4. Col 1-3：第4层中最大的3个绝对激活投射到2个不同图像的像素空间。注意，尽管模型是完全无监督的，但是如何重建不同的结构。有关识别用途的详细信息，请参阅第3节。 第4-5列：前3列的总和; 原始输入图像以及switches配置。 我们现在描述一种将此分解与SPM分类器结合使用的新颖方法。

对于每个图像，我们从顶层获取 M M 个最大绝对激活值的特征图，并将它们重构成 M M 个不同的图像 (y^i,1,...,y^i,M) ( y ^ i , 1 , . . . , y ^ i , M ) ，每个都包含由模型生成的各种图像部分。这对于具有大的接收域的高层是有意义的。在图4中，我们展示了针对2个不同图像推断的顶层 M=3 M = 3 的第4层激活的像素空重构建。注意它们如何包含由模型提取的选择图像结构的良好重构，同时抑制相邻内容，提供软分解。例如，脸部的第二个最大值重建左眼，嘴和左肩，但其他部分只有一些。相反，第三个最大值是重构头发。 每个最大重构中的结构由纹理区域（例如美洲狮的阴影）以及边缘结构组成。 他们也倾向于重构目标好于重构背景。

我们使用这些重构图对应的第一层特征图，而不是直接将 (y^i,1,...,y^i,M) ( y ^ i , 1 , . . . , y ^ i , M ) 输入到SPM中，因为该层的激活大致相当于非标准化的SIFT特征(标准SPM输入见[9])。为每个 z^i,M z ^ i , M 计算单独的金字塔后，我们平均这 M M 个金字塔表示一幅图像。我们也可以将SPM应用于实际的第一层特征图 zi1 z 1 i ，它们更加密集，甚至覆盖了图像4。这两部分的金字塔可以组合起来以提高性能。

4.Experiments

我们在Caltech-101数据集的全部3060张图像训练我们的模型(每类30张图像)。

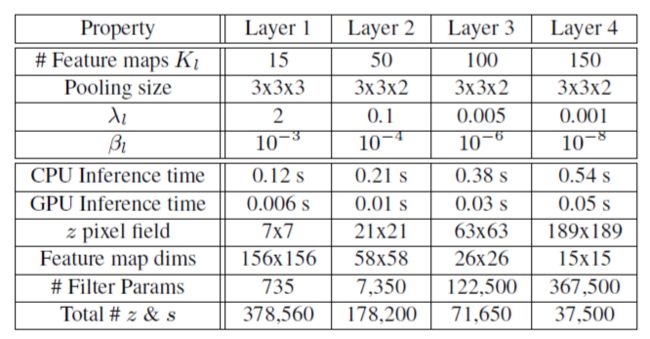
Table 1. 参数设置(上面4行)和模型统计(下面5行)

Pre-processing:
每个图像都转换为灰度，并调整为150 * 150（零填充以保持宽高比）。使用13 * 13高斯滤波器（a = 5）应用局部减法和除数归一化（即每个像素周围的补丁应具有零均值和单位范数）。

Model architecure:
我们使用4层模型，具有7×7个滤波器， E=10 E = 10 的训练迭代。各种参数，时间和统计数据如表1所示。由于有效的推理方案，我们的方法比其他方法如[3,8,11]能训练更多的特征图和更多的数据。通过第4层，每个特征图元素( z z 像素场)的接收域覆盖整个图像，使其适用于第3节中描述的新颖特征提取过程。在模型的较低层，该表示具有许多潜在变量（即 z z 和 s s ），但是层数升高， z z 和 s s 的数量反而减少。平衡这种趋势，过滤器参数的数量随着我们上升而大幅度增长，并且模型的顶层能够学习目标的特殊结构。

4.1.Model visualization

图5.a-d 通过缩放显示了所选特征的多样性，在模型的每层中学到的滤波器的可视化。e)相关接受域大小的图示。f)每层图像的重构。有关说明，请参见第4.1节。这个特征最好以电子形式查看。

我们的模型的自上而下的性质使其易于检查它已经学到了什么。 在图5中，我们通过单独获取每个特征图并在整个训练集中选择单个最大的绝对激活来可视化模型中的过滤器。使用特定的switches设置，我们将其投影到输入像素空间。在层1(图5(a))，我们看到一系列不同频率的定向Gabors算子和一些直流滤波器。在层2(图5(b))中，可以看到从第一层滤波器的组合构建的边缘连接和曲线。对于选择过滤器(以彩色突出显示)，我们展开以显示所有图像中的25个最强激活。每组显示出由特定激活的特定switches设置产生的某种程度的变化的聚类。参见例如T形结的滑动构型(蓝框)。反映其大的接收域，层3中的过滤器(图5(c))显示了一系列复杂的组成。突出显示的框显示了该模型能够聚类相当复杂的结构。注意，生成的分组与图像块的像素空间聚类完全不同，因为它们是：(i)形状上不同于矩形;(ii)利用下面的switches提供适应性的几何变换。第4层过滤器(图5(d))显示了具有相同类或相似形状的对象之间的分组的整个对象的完全重构。为了理解每个投影的相对尺寸，我们在图5(e)中还显示了层1-4的接收域。最后，图5(f)中显示了4个示例的输入图像模型的每层重构。请注意，与Lee等人[11]的相关模型不同，甚至在第4层重构中仍保留了清晰的图像边缘。

4.2.Evaluation on Caltech-101

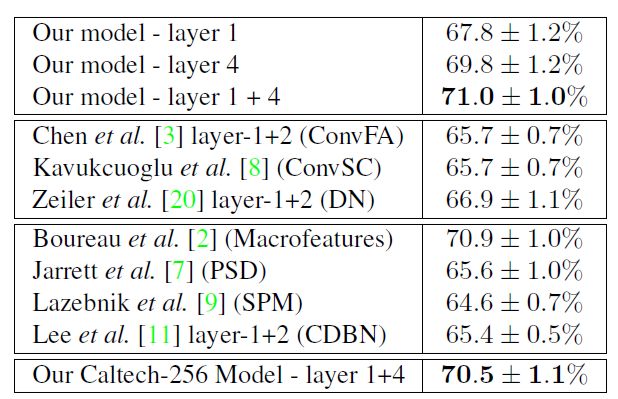
表2 Caltech-101的识别性能与其他按相似度分组的方法相比较(从上至上)。第1组：我们的方法;组2：SPM分类器的相关卷积稀疏编码方法;组3：使用SPM分类器的其他方法;组4：我们的模型采用在Caltech-256图像集上训练的过滤器

表3.模型的Caltech-256识别性能和类似的SPM方法。还对Caltech-101模型进行了评估。

使用我们的模型中的 M=50 M = 50 分解来产生用于训练Lazebnik等人[9]的空间金字塔匹配(SPM)分类器的输入。 Caltech-101测试仪的分类结果如表2所示.(在表2和表3中，我们仅考虑基于单一特征类型的方法。将数百种不同特征与多种内核学习方法相结合的方法胜过所列出的方法。)

将SPM分类器应用于我们模型的特征 z1 z 1 ，与许多其他方法(包括使用卷积稀疏编码的方法)(表2中的第二组)产生类似的结果(67.8％)。然而，如第3节所述，使用SPM分类器中第4层的50个最大分解，我们获得了2％的显着性能提升，超过了大多数也使用SPM分类器(表2中间两个)的分层和稀疏编码方法。从第4层和第1层特征的最大激活产生的SVM核求和，我们达到71.0％。基于具有可比性能的SPM的唯一方法是Boureau等人[2]基于宏观特征提出的。目前最先进的技术[2,19,17]是使用描述符软量化的形式，替代在SPM中使用的硬k均值量化(例如Wang等人[17]使用基于稀疏编码的分类器获得73.4％)。

4.3.Evaluation on Caltech-256

使用与Caltech-101相同的训练和评估参数，我们在更困难的Caltech-256数据集上评估了我们的模型(见表3)。通过在256个类别中的每30个图像上训练我们的模型，并使用 M=50 M = 50 分解，如前所述，采用SPM分类器，我们得到超过SIFT特征3.7％的性能提升。

4.4.Transfer learning

通过使用Caltech-101训练了的过滤器，然后对Caltech-256进行分类，反之亦然，我们可以测试我们的模型如何推广到新图像。在这两种情况下，分类表现仍然存在原始结果中的错误(见表2和表3)，显示了我们的模型适用于新实例和全新类的适应性。

4.5.Classification and reconstruction relationship

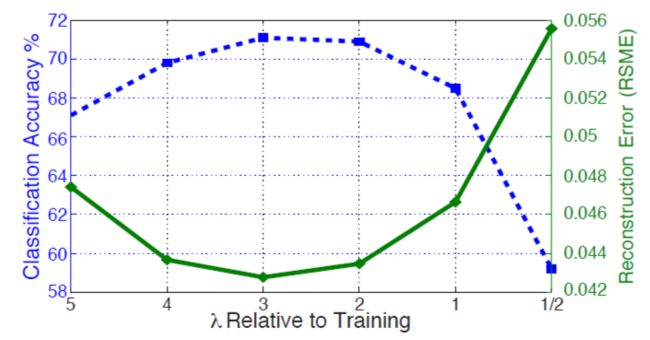
图6.不同稀疏度的重构(实线)和分类精度(虚线)之间的关系。

虽然我们已经表现出稀疏性对于学习高级特征并将图像分解成零件的层次结构是有用的，但是它不一定是Rigamonti等人[14]分类的强力提示。通过改变每层的 λl λ l 参数进行推理，保持滤波器固定，我们在图6分析了Caltech-101中稀疏度和分类性能的折衷。具有较高的 λl λ l ，稀疏性降低，重构得到提升，识别率提高。最佳出现在用于训练的 λl λ l 的3倍左右，之后增加了ISTA导致更大的ISTA步骤，该步骤引入优化中的不稳定性.(表2和表3的结果使用的是 2∗λl 2 ∗ λ l )

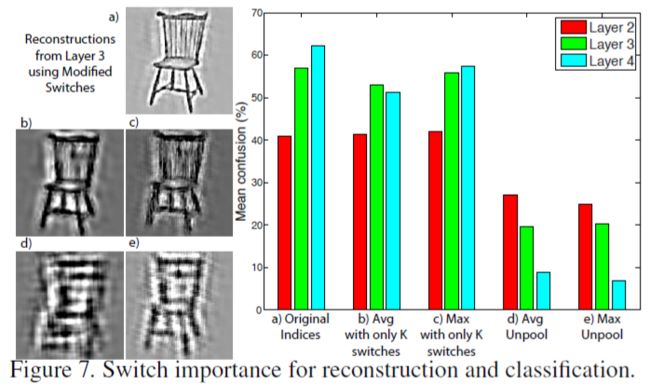
4.6.Analysis of switch settings

其他深层模型缺乏明确的switches，因此在重构过程中将单个激活放置在每个池的中心[3]，或将其均匀分布在所有位置[11]。图7演示了switches的实用性：我们(i)使用层2,3和4中的前25个激活来重构不同形式的switches行为;(ii)对所得到的重构进行求和(iii)使用第1层特征(如前所述)对Caltech-101进行分类。

图7 重构和分类的switches重要性

从图7(a)所示的层3重构显而易见，保留所有最大位置允许锐化重构，却平均了unpooling。图7(b,d)导致模糊，并使用最大unpooling中的中心指数。图7(c,e)导致抖动与识别性能相应降低重构时，保持正确的k个switches。图7(b,c)对于在较低层中选择适当的特征图是至关重要的，因此防止物体的极端变形(见图7(d,e))，导致识别性能严重降低。

5.Discussion

本文介绍的新颖方法使我们可以可靠地学习具有多层次的模型。当我们上升层时，我们的模型中的switches允许滤波器适应日益变化的输入模式。因此，该模型能够捕获在类之间泛化的中级和高级特征。使用这些功能与标准分类器在Caltech-101和Caltech-256提供了极具竞争力的精度。 我们学习的代表性的一般性通过其能够将其未被训练的数据集概括为一体，同时保持可比性能。 我们的算法的Matlab代码可在www.matthewzeiler.com/pubs/iccv2011/获取。

注：由于原链接失效，这里给出百度云的链接: https://pan.baidu.com/s/1CU9fLu0R9NOCWv74kgXb2Q 密码: e9fr

References

[1] A. Beck and M. Teboulle. A fast iterative shrinkagethresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences, 2(1):183–202, 2009.
[2] Y. Boureau, F. Bach, Y. LeCun, and J. Ponce. Learning midlevel features for recognition. In CVPR. IEEE, 2010. 7
[3] B. Chen, G. Sapiro, D. Dunson, and L. Carin. Deep learning with hierarichal convolutional factor analysis. JMLR, page
Submitted, 2010. 1, 2, 5, 7, 8
[4] S. Fidler, M. Boben, and A. Leonardis. Similarity-based cross-layered hierarchical representation for object categorization.
In CVPR, 2008. 2
[5] C. E. Guo, S. C. Zhu, and Y. N.Wu. Primal sketch: Integrating texture and structure. CVIU, 106:5–19, 2007. 2
[6] G. E. Hinton, S. Osindero, and Y. W. Teh. A fast learning algorithm for deep belief nets. Neural Comput., 18(7):1527–1554, 2006. 1, 2
[7] K. Jarrett, K. Kavukcuoglu, M. Ranzato, and Y. LeCun. What is the best multi-stage architecture for object recognition? In ICCV, 2009. 2, 7
[8] K. Kavukcuoglu, P. Sermanet, Y. Boureau, K. Gregor, M. Mathieu, and Y. LeCun. Learning convolutional feature hierachies for visual recognition. In NIPS, 2010. 1, 2, 5, 7
[9] S. Lazebnik, C. Schmid, and J. Ponce. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. In CVPR, 2006. 4, 5, 7
[10] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradientbased learning applied to document recognition. IEEE, 86(11):2278–24, 1998. 2
[11] H. Lee, R. Grosse, R. Ranganath, and A. Y. Ng. Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations. In ICML, pages 609–616,2009. 1, 2, 5, 7, 8
[12] M. Ranzato, F. Huang, Y. Boureau, and Y. LeCun. Unsupervised learning of invariant feature hierarchies with applications to object reocgnition. In CVPR, 2007. 2
[13] M. Riesenhuber and T. Poggio. Hierarchical models of object recognition in cortex. Nature Neuroscience, 2(11):1019–1025, 1999. 2
[14] R. Rigamonti, M. Brown, and V. Lepetit. Are sparse representations really relevant for image classification? In CVPR, pages 1545–1552, 2011. 7
[15] T. Serre, L. Wolf, and T. Poggio. Object recognition with features inspired by visual cortex. In CVPR, 2005. 2
[16] Z.W. Tu and S. C. Zhu. Parsing images into regions, curves, and curve groups. IJCV, 69(2):223–249, August 2006. 2
[17] J. Wang, J. Yang, K. Yu, T. Huang, and Y. Gong. Localityconstrained linear coding for image classification. In CVPR, 2010. 7
[18] S.Winder, G. Hua, and M. Brown. Picking the best daisy. In CVPR, 2009. 1
[19] J. Yang, K. Yu, Y. Gong, and T. Huang. Linear spatial pyramid matching using sparse coding for image classification. In CVPR, 2009. 7
[20] M. Zeiler, D. Krishnan, G. Taylor, and R. Fergus. Deconvolutional networks. In CVPR, 2010. 1, 2, 7
[21] L. Zhu, Y. Chen, and A. L. Yuille. Learning a hierarchical deformable template for rapid deformable object parsing. PAMI, March 2009. 2
[22] S. Zhu and D. Mumford. A stochastic grammar of images. Foundations and Trends in Comp. Graphics and Vision, 2(4):259–362, 2006. 2