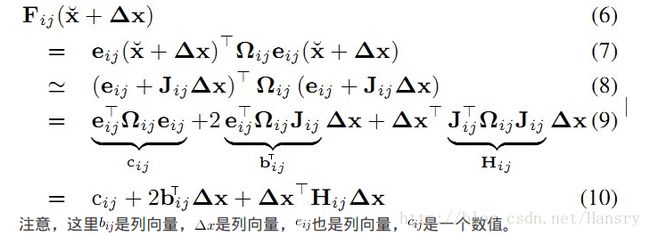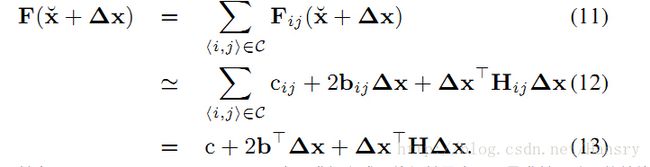SLAM——图优化篇

1.图优化的入门

在上节中，直接用俩俩匹配搭建一个里程计，但是如果：1.错误匹配，整个图就会看起来很奇怪，就是错了。2.误差会累积，常见的现象是：相机转过去的过程能作对，但转回来就很奇怪。3.效率低。由于地图拼接中累计误差是个很严重的问题，所以要保证每次匹配都精确无误，而这是很难实现的。所以我们把所有整的信息都考虑进来，成为一个全slam问题。

姿态图（原理部分）
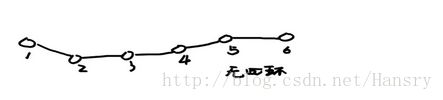
姿态图，是由相机姿态构成的一个图（graph）。这里的图，从图论意义上来说，一个图有节点（位姿）和边构成（R，t）

在最简单的情况下节点代表相机的各个位姿（四元数或者矩阵）： p=[x,y,z,qx,qy,qz,qw] p = [ x , y , z , q x , q y , q z , q w ]

而边则代表各个位姿的转换关系： T=[R3×30t3×11] T = [ R 3 × 3 t 3 × 1 0 1 ]

则我们对于简单的回环来说可以大概表示为: 1→21T2→32T3→43T4 1 → 1 2 T 2 → 2 3 T 3 → 3 4 T 4

用高博的图即：

像这样子的vo，我们除了对边进行优化之外，没有比较好的方法了，构造最小二乘法问题，使得整个VO的边误差最小，则有:

minR,t=minE=∑i,j||xi−Ti,jxj||22 m i n R , t = m i n E = ∑ i , j | | x i − T i , j x j | | 2 2

于是，我们的工作转移到了对代价函数： xi−Ti,jxj x i − T i , j x j 进行最小优化。

怎么把SLAM问题表示成图呢？

（参考高博的博客加上自己的一些理解）
图：顶点（需要调整的变量，即最小二乘中的决策变量）和边（观测方程z（测出来的东西）），然后我们是以 ek=zk−h(xk) e k = z k − h ( x k ) 为误差，以 minxFk(xk)=|ek| m i n x F k ( x k ) = | e k | 为目标函数。

那么优化变量（即顶点）： 可以是一个机器人的pose（6自由度下为4x4的变换矩阵T或者3自由度下的x,y,）也可以是一个空间点（三维空间的[x,y,z]或者二维像素的[x,y]）。观测方程（这里的观测方程，我之前纠结了好久，但是通俗的讲就是你传感器测出来的数据计算出的你想要求的变量）也有很多形式：
1.机器人俩个Pose之间的变换；
2.机器人在某个Pose处用激光测量到了某个空间点，得到了它离自己的距离和角度。
3.机器人在某个Pose处用相机观测到了某个空间点，得到了它的像素坐标。

在图中，以顶点为优化变量（在最小二乘中为决策变量），以边为观测方程（就是测出来的东东）。由于边可以链接一个或多个顶点，所以我们把它的形式写成更广义的 zk=h(xk1,xk2,...) z k = h ( x k 1 , x k 2 , . . . ) ，以不限制顶点数量的意思。
1.机器人俩个pose之间的变换；——一条Binary Edge(二元边)，边的方程为： T1=ΔT⋅T2 T 1 = Δ T ⋅ T 2
2.机器人在某个Pose处用相机观测到了某个空间点，得到它的像素坐标；——Binary Edge，顶点为一个3D Pose：T和一个空间点 x=[x,y,z]T x = [ x , y , z ] T ，观测数据为像素坐标 z=[u,v]T z = [ u , v ] T ,观测方程为： z=C(Rx+t) z = C ( R x + t )

总而言之，顶点就是优化变量（三维空间点或者Pose），边就是观测方程（T或者二维坐标）

2.图优化的深入理解

图优化是什么？在graph-based SLAM中，机器人的位姿是一个节点或顶点（vetex），位姿之间的关系构成边（edge），比如t+1时刻和t时刻之间的odometry关系构成边，或者由视觉计算出来的位姿转换矩阵也可以构成边。一旦图构成了，就要调整机器人的位姿去尽量满足这些边构成约束。

图优化SLAM能分解成俩个任务：
1.构建图，机器人位姿当做顶点，位姿关系当做边，称为前端。
2.优化图，调整机器人位姿顶点尽量满足边的约束，称为后端。

图优化过程中：先堆积数据，机器人位姿为构建的顶点。边是位姿之间的关系，可以是编码器数据计
算的位姿，也可以是通过ICP匹配计算出来的位姿，还可以是闭环检测的位姿关系。

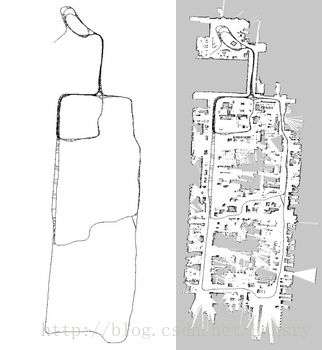
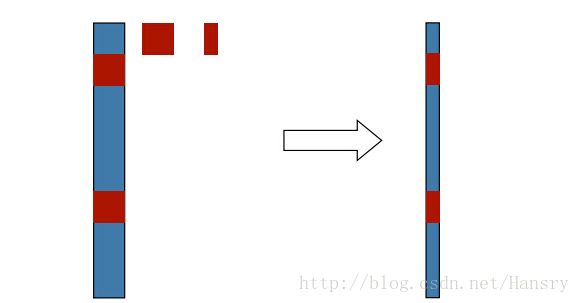
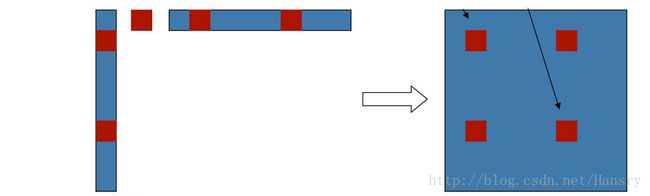
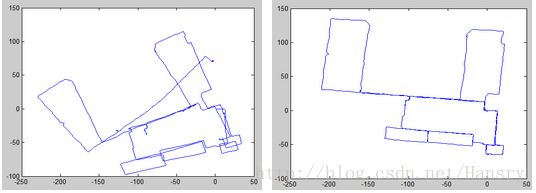
左图为建完图未经优化的图，而右图为调整顶点满足边的约束，最后得到的地图。

—————一个帮助理解的例子：——————–
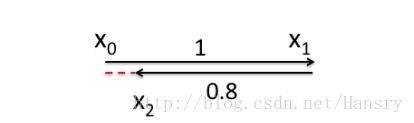
如下图所示，假如机器人初始点在0处，然后机器人向前移动，通过编码器测得是1，再编码器又测得了它向后0.8，结果通过闭环检测却发现它又回到了起点。可以看出，编码器出现了点小问题，那么需要机器人这几个状态中的位姿到底是怎么样的才最好的满足这些条件呢？

建立关系：
f1=x0=0;f2=x1−x0−1=0;f3=x2−x1+0.8=0;f4=x2−x0=0 f 1 = x 0 = 0 ; f 2 = x 1 − x 0 − 1 = 0 ; f 3 = x 2 − x 1 + 0.8 = 0 ; f 4 = x 2 − x 0 = 0

为了使的总体的误差最小，使用最小二乘如下：
∑4i=1||fi||22=∑4i=1f2i=x20+(x1−x0−1)2+(x2−x1+0.8)2+(x2−x0)2 ∑ i = 1 4 | | f i | | 2 2 = ∑ i = 1 4 f i 2 = x 0 2 + ( x 1 − x 0 − 1 ) 2 + ( x 2 − x 1 + 0.8 ) 2 + ( x 2 − x 0 ) 2

为了使残差平方和最小，我们对上面的函数每个变量求偏导（雅克比矩阵），并使得偏导等于0；

∂c∂x0=2x0−2(x1−x0−1)−2(x2−x0)=0; ∂ c ∂ x 0 = 2 x 0 − 2 ( x 1 − x 0 − 1 ) − 2 ( x 2 − x 0 ) = 0 ;

∂c∂x1=2(x1−x0−1)−2(x2−x1+0.8)=0; ∂ c ∂ x 1 = 2 ( x 1 − x 0 − 1 ) − 2 ( x 2 − x 1 + 0.8 ) = 0 ;

∂c∂x2=2(x2−x1+0.8)+2(x2−x0)=0; ∂ c ∂ x 2 = 2 ( x 2 − x 1 + 0.8 ) + 2 ( x 2 − x 0 ) = 0 ;

通过解答求得 x0=0 x 0 = 0 ， x1=0.93 x 1 = 0.93 ， x2=0.07 x 2 = 0.07 ；即对整体进行了优化，从而使得误差项最小。

求机器人SLAM过程中最优轨迹可以表示成求解机器人位姿使得下面误差平方函数最小

F(x)=∑i,j∈Ce(xi,xj,zi,j)Ωi,je(xi,xj,zi,j) F ( x ) = ∑ i , j ∈ C e ( x i , x j , z i , j ) Ω i , j e ( x i , x j , z i , j ) ——目标函数

其中 xi,xj x i , x j 均表示机器人的位姿， zij z i j 表示测量值， Ωi,j Ω i , j 即所谓的权重矩阵。

对于上述的最小二乘问题可以从最大似然角度解释。对于传感器的测量，我们可以假设它受高斯白噪声的影响，所以每一个测量值的分布可以看作是以真值为中心的高斯分布。如果测量是多变的，那么就是多元高斯分布：

N(x1,x2,...,xn)=1(2π)kΣexp(−12(x−u)TΣ−1(x−u)) N ( x 1 , x 2 , . . . , x n ) = 1 ( 2 π ) k Σ e x p ( − 1 2 ( x − u ) T Σ − 1 ( x − u ) )

*其中，假设x是m维高维变量，且每一维中有N个属性，那么x为mxn维矩阵，而重点内容u由于是均值，所以是u是m维向量，则协方差矩阵是mxm矩阵（通俗点可以理解：只有方阵才有逆矩阵，在某个场合不适用）。多元高斯分布的协方差矩阵的某一维越大，高斯曲线越矮胖，表示在这个方向上越不确定。对于某个测量，我们应该使它出现在概率最大的地方，这时候又要拿出贝叶斯公式了： P(x|z)=p(z|x)p(x)p(z) P ( x | z ) = p ( z | x ) p ( x ) p ( z )

其中 p(z|x) p ( z | x ) 为最大似然， p(x) p ( x ) 为先验， p(x|z) p ( x | z ) 为后验，这里我们优化的其实就只是最大似然，可以理解为“观测到这个数据z（即观测方程，即边，即T）,x（机器人位姿）最可能出现的地方”*

则最大似然概率的log形式的计算公式为：

lij∝[zij−z∧ij(xi,xj)]TΩij[zij−z∧ij(xi,xj)] l i j ∝ [ z i j − z ∧ i j ( x i , x j ) ] T Ω i j [ z i j − z ∧ i j ( x i , x j ) ]

上式和前面的误差平方和函数很想只不过这里显示的指明了误差函数的形式，所以，误差的权重矩阵等于协方差矩阵的逆矩阵。由于图优化每一条边都代表一个测量值，如转换矩阵T。所以图优化里每一条边的信息矩阵就是测量协方差矩阵的逆，如果协方差越小，则说明越值得相信，信息权重越大（协方差知识链接：http://blog.csdn.net/Hansry/article/details/77800555）

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<我是分割线

然后误差项 e(xi,yi,zij)是一个向量误差函数表示xi和xj之间的关系与测量 zi,j的符合程度。

为了对后面进行简化，将误差函数写成下面的形式： e(xi,xj,zi,j)=def.ei,j(xi,xj)=def.ei,j(x) e ( x i , x j , z i , j ) = d e f . e i , j ( x i , x j ) = d e f . e i , j ( x )

求解的方法是把误差函数在该初始值x0（假设我们已经有了好的假设值）附近进行一阶泰勒展开：
则有： ei,j(xi+△x,xj+△x)=eij(x0+△x)≈eijx0+Jijx0Δx e i , j ( x i + △ x , x j + △ x ) = e i j ( x 0 + △ x ) ≈ e i j x 0 + J i j x 0 Δ x (上式可看出雅克比矩阵J是横向量)

其中 Jij J i j 是雅克比矩阵来着。

将该误差泰勒展开式代入到目标函数中，可得：

（上式的矩阵第二个步还没搞懂清楚其运算）

将与(10)式代入，可以重写误差平方和函数如下：

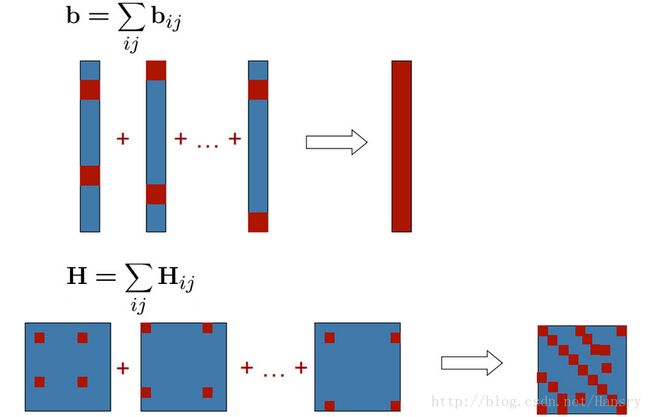
其实就是对其进行求和,其中 c=∑cij,b=∑bij,H=∑Hij c = ∑ c i j , b = ∑ b i j , H = ∑ H i j 。为了求解上式，使得其最小，还是求其一阶导数并使其等于0，可以得：

HΔx∗=−b H Δ x ∗ = − b （这里的H是mxm矩阵，b为mx1向量）

这里H是系统的信息矩阵（注意与边的信息矩阵 Ω Ω 区别），系统的解就是在初始值上叠加这个增量:

x∗=x0+Δx∗ x ∗ = x 0 + Δ x ∗

（这个时候的加法其实并不一定正确，因为如果优化变量为pose，则旋转矩阵对加法是不封闭的，这里需要酌情处理）

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<我是分割线

对于上述的b,H,雅克比矩阵，我们需要弄清楚它的结构，对于单条边的雅克比矩阵来说：

知道了雅克比矩阵的结构后，再来看看b和H矩阵，由于 bij b i j 为列向量，可以知道:

bTij=eTijΩijJij=eTijΩij(0...Aij...Bij...0)=(0...eTijΩijAij...eTijΩijBij...0) b i j T = e i j T Ω i j J i j = e i j T Ω i j ( 0... A i j . . . B i j . . .0 ) = ( 0... e i j T Ω i j A i j . . . e i j T Ω i j B i j . . .0 )

则bij是列向量，如下：

bij=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⋮ATijΩijeij⋮BTijΩijeij⋮⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟ b i j = ( ⋮ A i j T Ω i j e i j ⋮ B i j T Ω i j e i j ⋮ )

Hij=JTijΩijJij=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⋮ATij⋮BTij⋮⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟Ωij(⋯Aij⋯Bij⋯) H i j = J i j T Ω i j J i j = ( ⋮ A i j T ⋮ B i j T ⋮ ) Ω i j ( ⋯ A i j ⋯ B i j ⋯ )

则有全部的：

由上可知，对于所有的位姿，根据其雅克比矩阵和海塞矩阵，可以找到最优的位姿来拟合其位姿，即根据约束来优化位姿。

3.Matlab仿真并图优化分析

图优化的前端（这里是激光的）：
1.当机器人前进0.5m或者旋转超过0.5弧度时，将新的机器人位姿添加到图的顶点，并且记录相应的激光数据。
2.当前激光数据和上一次的激光数据进行匹配，获得俩个相邻位姿之间的变换关系，将该变换关系加入到图的边。
3.当机器人重新回到一个已知区域时，激光数据和以前的诺干数据进行匹配进行闭环检测。如果匹配成功，则在相应顶点之间加入一条边。

图优化后端：
1.构建误差函数：如果是2D SLAM，则我们知道机器人的某一位姿可以表达为: xTi=(xi,yi,θ) x i T = ( x i , y i , θ ) ,在各类论文中，把误差函数设定为如下形式：

eij(xi,xj)=t2v(Z−1ij(X−1i⋅Xj)) e i j ( x i , x j ) = t 2 v ( Z i j − 1 ( X i − 1 ⋅ X j ) ) （其中 Z−1ij Z i j − 1 表示measurement，其中 X−1i⋅Xj X i − 1 ⋅ X j 表示俩个相联位姿）

并且上式中 Xi X i 和 Xi X i 是位姿向量 xi x i , xj x j 的矩阵形式，使用一个v2t()的函数就行了。

其中要注意的是， X−1i⋅Xj X i − 1 ⋅ X j 表示位姿j到位姿i之间的变换矩阵 Z∧ij Z ∧ i j ，这个公式的推导为： Xwi X w i 表示i到w的转换关系， Xwj X w j 表示j到w的转换关系，则 X−1wi⋅Xwj=Xiw⋅Xwj=Xij X w i − 1 ⋅ X w j = X i w ⋅ X w j = X i j

为什么测量出的转换矩阵和理论计算的转换矩阵的误差error要这样子计算？

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<我是分割线

矩阵求逆的知识：
分块矩阵如何求逆：

[R0t1]−1=[[I0t1][R001]]−1=[[R0t1]−1[I0−t1]−1]=[[RT0t1][I0−t1]]=[RT0−RTt1] [ R t 0 1 ] − 1 = [ [ I t 0 1 ] [ R 0 0 1 ] ] − 1 = [ [ R t 0 1 ] − 1 [ I − t 0 1 ] − 1 ] = [ [ R T t 0 1 ] [ I − t 0 1 ] ] = [ R T − R T t 0 1 ]

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<我是分割线

假设j到i的变换矩阵估计值 Z∧ij Z ∧ i j 为 X−1i⋅Xj X i − 1 ⋅ X j 。i，j之间变换的测量值变换矩阵为： Zij=[R′0t′1] Z i j = [ R ′ t ′ 0 1 ]

误差计算：

上式需要注意的是： Zij Z i j 表示的是测量值的变换矩阵，而 X−1iXj X i − 1 X j 表示计算的j到i的转换矩阵。（这个很重要，含义使得整条式子成立）

旋转矩阵R表示逆时针旋转， R′T R ′ T 表示顺时针旋转， R′TR R ′ T R 俩个旋转矩阵相乘再向量化的物理意义就是俩个旋转矩阵角度的差异（注意这里还没有对其向量化）。 R′T(t−t′) R ′ T ( t − t ′ ) 表示俩个位移向量的差异。

具体代码即以这种向量方式进行优化的见博客：http://blog.csdn.net/heyijia0327/article/details/47428553

运行完的代码主要是如下所示：

参考博客：
http://blog.csdn.net/heyijia0327/article/details/47428553
http://www.cnblogs.com/gaoxiang12/p/5244828.html