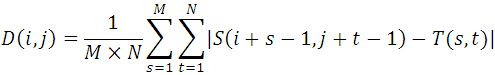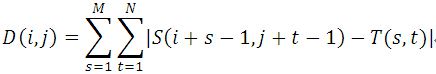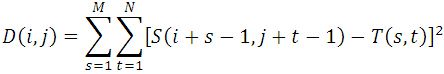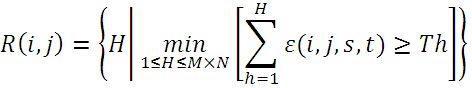图像匹配算法 MAD、SAD、SSD、MSD、NCC、SSDA、SATD,LBD算法

图像匹配算法分为3类：基于灰度的匹配算法、基于特征的匹配算法、基于关系的匹配算法

（1）基于灰度的模板匹配算法：模板匹配（Blocking Matching）是根据已知模板图像到另一幅图像中寻找与模板图像相似的子图像。基于灰度的匹配算法也称作相关匹配算法，用空间二维滑动模板进行匹配，不同匹配算法主要体现在相关准则的选择方面，常见的基于模板的匹配算法可以参考下面的链接：

参考：http://blog.csdn.net/hujingshuang/article/details/47759579

（2）基于特征的匹配算法：首先提取图像的特征，再生成特征描述子，最后根据描述子的相似程度对两幅图像的特征之间进行匹配。图像的特征主要可以分为点、线（边缘）、区域（面）等特征，也可以分为局部特征和全局特征。

区域（面）特征提取比较麻烦，耗时，因此主要用点特征和边缘特征。

点特征包括：Harris 、Moravec、KLT、SIFT、SURF 、BRIEF、SUSAN、FAST、CENSUS、FREAK（点击打开链接）、BRISK（点击打开链接）、ORB、光流法（点击打开链接）、A-KAZE等。

边缘特征包括：LoG算子、Robert算子、Sobel算子、Prewitt算子、Canny算子等。

 光流法：

（3）基于关系的匹配算法：建立语义的网络，是人工智能领域在图像处理中的应用，但还没有突破性的进展。

 

立体匹配：左右相机的匹配，用基于灰度的模板匹配方法，对所有的像素点匹配。

跟踪匹配：前后帧的匹配，用基于特征的匹配算法，对特征点进行匹配，然后根据几个匹配的特征点计算出相机的位姿.

基于灰度的模板匹配算法（一）：MAD、SAD、SSD、MSD、NCC、SSDA、SATD算法

简介：

       本文主要介绍几种基于灰度的图像匹配算法：平均绝对差算法（MAD）、绝对误差和算法（SAD）、误差平方和算法（SSD）、平均误差平方和算法（MSD）、归一化积相关算法（NCC）、序贯相似性检测算法（SSDA）、hadamard变换算法（SATD）。下面依次对其进行讲解。

MAD算法

介绍

        平均绝对差算法（Mean Absolute Differences，简称MAD算法），它是Leese在1971年提出的一种匹配算法。是模式识别中常用方法，该算法的思想简单，具有较高的匹配精度，广泛用于图像匹配。

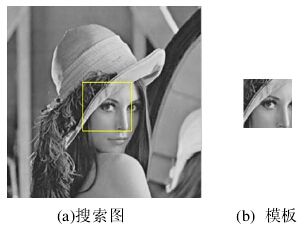
设S(x,y)是大小为mxn的搜索图像，T(x,y)是MxN的模板图像，分别如下图(a)、(b)所示，我们的目的是：在(a)中找到与(b)匹配的区域（黄框所示）。

算法思路

        在搜索图S中，以(i,j)为左上角，取MxN大小的子图，计算其与模板的相似度；遍历整个搜索图，在所有能够取到的子图中，找到与模板图最相似的子图作为最终匹配结果。

        MAD算法的相似性测度公式如下。显然，平均绝对差D(i,j)越小，表明越相似，故只需找到最小的D(i,j)即可确定能匹配的子图位置：

其中：

算法评价：

优点：

①思路简单，容易理解（子图与模板图对应位置上，灰度值之差的绝对值总和，再求平均，实质：是计算的是子图与模板图的L1距离的平均值）。

②运算过程简单，匹配精度高。

缺点：

①运算量偏大。

②对噪声非常敏感。

——————————————————————————————————————————————————————————————————————————————

SAD算法

介绍

        绝对误差和算法（Sum of Absolute Differences，简称SAD算法）。实际上，SAD算法与MAD算法思想几乎是完全一致，只是其相似度测量公式有一点改动（计算的是子图与模板图的L1距离），这里不再赘述。

算法实现

由于文章所介绍的几个算法非常相似，所以本文仅列出SAD算法的代码，其余算法的实现类似。看别人代码都相对费力，想自己敲也很简单。

MATLAB代码

 

1. %%

2. %绝对误差和算法（SAD）

3. clear all;

4. close all;

5. %%

6. src=imread('lena.jpg');

7. [a b d]=size(src);

8. if d==3

9. src=rgb2gray(src);

10. end

11. mask=imread('lena_mask.jpg');

12. [m n d]=size(mask);

13. if d==3

14. mask=rgb2gray(mask);

15. end

16. %%

17. N=n;%模板尺寸，默认模板为正方形

18. M=a;%代搜索图像尺寸，默认搜索图像为正方形

19. %%

20. dst=zeros(M-N,M-N);

21. for i=1:M-N %子图选取，每次滑动一个像素

22. for j=1:M-N

23. temp=src(i:i+N-1,j:j+N-1);%当前子图

24. dst(i,j)=dst(i,j)+sum(sum(abs(temp-mask)));

25. end

26. end

27. abs_min=min(min(dst));

28. [x,y]=find(dst==abs_min);

29. figure;

30. imshow(mask);title('模板');

31. figure;

32. imshow(src);

33. hold on;

34. rectangle('position',[y,x,N-1,N-1],'edgecolor','r');

35. hold off;title('搜索图');

 

输出结果

——————————————————————————————————————————————————————————————————————————————

SSD算法

        误差平方和算法（Sum of Squared Differences，简称SSD算法），也叫差方和算法。实际上，SSD算法与SAD算法如出一辙，只是其相似度测量公式有一点改动（计算的是子图与模板图的L2距离）。这里不再赘述。

——————————————————————————————————————————————————————————————————————————————

MSD算法

        平均误差平方和算法（Mean Square Differences，简称MSD算法），也称均方差算法。实际上，MSD之余SSD，等同于MAD之余SAD（计算的是子图与模板图的L2距离的平均值），故此处不再赘述。

 

————————————————————————————————————————————————————————————————————————————————

NCC算法

        归一化积相关算法（Normalized Cross Correlation，简称NCC算法），与上面算法相似，依然是利用子图与模板图的灰度，通过归一化的相关性度量公式来计算二者之间的匹配程度。

其中，、分别表示(i,j)处子图、模板的平均灰度值。

————————————————————————————————————————————————————————————————————————

SSDA算法

        序贯相似性检测算法（Sequential Similiarity Detection Algorithm，简称SSDA算法），它是由Barnea和Sliverman于1972年，在文章《A class of algorithms for fast digital image registration》中提出的一种匹配算法，是对传统模板匹配算法的改进，比MAD算法快几十到几百倍。

与上述算法假设相同：S(x,y)是mxn的搜索图，T(x,y)是MxN的模板图，是搜索图中的一个子图（左上角起始位置为(i,j)）。

显然：，

SSDA算法描述如下：

①定义绝对误差：

其中，带有上划线的分别表示子图、模板的均值：

实际上，绝对误差就是子图与模板图各自去掉其均值后，对应位置之差的绝对值。

②设定阈值Th；

③在模板图中随机选取不重复的像素点，计算与当前子图的绝对误差，将误差累加，当误差累加值超过了Th时，记下累加次数H，所有子图的累加次数H用一个表R(i,j)来表示。SSDA检测定义为：

下图给出了A、B、C三点的误差累计增长曲线，其中A、B两点偏离模板，误差增长得快；C点增长缓慢，说明很可能是匹配点（图中Tk相当于上述的Th，即阈值；I(i,j)相当于上述R(i,j)，即累加次数）。

④在计算过程中，随机点的累加误差和超过了阈值（记录累加次数H）后，则放弃当前子图转而对下一个子图进行计算。遍历完所有子图后，选取最大R值所对应的(i,j)子图作为匹配图像【若R存在多个最大值（一般不存在），则取累加误差最小的作为匹配图像】。

        由于随机点累加值超过阈值Th后便结束当前子图的计算，所以不需要计算子图所有像素，大大提高了算法速度；为进一步提高速度，可以先进行粗配准，即：隔行、隔离的选取子图，用上述算法进行粗糙的定位，然后再对定位到的子图，用同样的方法求其8个邻域子图的最大R值作为最终配准图像。这样可以有效的减少子图个数，减少计算量，提高计算速度。

——————————————————————————————————————————————————————————————————————

SATD算法

       hadamard变换算法（Sum of Absolute Transformed Difference，简称SATD算法），它是经hadamard变换再对绝对值求和算法。hadamard变换等价于把原图像Q矩阵左右分别乘以一个hadamard变换矩阵H。其中，hardamard变换矩阵H的元素都是1或-1，是一个正交矩阵，可以由MATLAB中的hadamard(n)函数生成，n代表n阶方阵。

      SATD算法就是将模板与子图做差后得到的矩阵Q，再对矩阵Q求其hadamard变换（左右同时乘以H，即HQH），对变换都得矩阵求其元素的绝对值之和即SATD值，作为相似度的判别依据。对所有子图都进行如上的变换后，找到SATD值最小的子图，便是最佳匹配。

MATLAB实现：

1. %//*****************************************

2. %//Copyright (c) 2015 Jingshuang Hu

3.  

4. %//@filename:demo.m

5. %//@datetime:2015.08.20

6. %//@author:HJS

7. %//@e-mail:[email protected]

8. %//@blog:http://blog.csdn.net/hujingshuang

9. %//*****************************************

10. %%

11. %//SATD模板匹配算法-哈达姆变换(hadamard)

12. clear all;

13. close all;

14. %%

15. src=double(rgb2gray(imread('lena.jpg')));%//长宽相等的

16. mask=double(rgb2gray(imread('lena_mask.jpg')));%//长宽相等的

17. M=size(src,1);%//搜索图大小

18. N=size(mask,1);%//模板大小

19. %%

20. hdm_matrix=hadamard(N);%//hadamard变换矩阵

21. hdm=zeros(M-N,M-N);%//保存SATD值

22. for i=1:M-N

23. for j=1:M-N

24. temp=(src(i:i+N-1,j:j+N-1)-mask)/256;

25. sw=(hdm_matrix*temp*hdm_matrix)/256;

26. hdm(i,j)=sum(sum(abs(sw)));

27. end

28. end

29. min_hdm=min(min(hdm));

30. [x y]=find(hdm==min_hdm);

31. figure;imshow(uint8(mask));

32. title('模板');

33. figure;imshow(uint8(src));hold on;

34. rectangle('position',[y,x,N-1,N-1],'edgecolor','r');

35. title('搜索结果');hold off;

36. %//完

 

输出结果：

—————————————————————————————————————————————————————————————————————

OK，介绍完毕，以上便是几种常见的基于灰度的模板匹配算法。

参考文献：

1、D.I BARNEA, H.F SILVERMAN, A class of algorithms for fast digital image registration[J], IEEE TRANSACTIONS ON COMPUTERS,1972.

2、赵启, 图像匹配算法研究[D], 2013.

3、丁慧珍, 抗任意角度旋转灰度匹配方法研究[D], 2006.

4、陈皓, 马彩文等, 基于灰度统计的快速模板匹配算法[J], 光子学报, 2009.

5、杨小冈等, 基于相似度比较的图像灰度匹配算法研究[J], 系统工程与电子技术, 2005.

LBD算法 - Graph matching 图匹配算法分析

概述

---

原文：《An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency》

上一步我们进行了线特征的提取和描述，接下来我们进行线特征的匹配。在此之前我们先通过预处理将一些明显无法匹配的特征给消除，以降低图匹配问题的维度。
该部分图匹配算法分为三步：

1. 查找候选匹配对
2. 构建关系图
3. 生成最终匹配结果

1. 查找候选匹配对

---

匹配的双方，我们分别称为参考图像和查询图像，检测出双方的LineVecs之后，我们要检测他们的一元几何属性和局部外观相似度，若未通过测试，那么认为他们是不匹配的。这样做可以大大减小图优化匹配的问题维度，使得我们后期匹配的速度更快。

1.1.一元几何属性

线段的一元几何属性就是LineVecs的方向，在同一个LineVec中的线具有相同的方向，并且每一个LineVec拥有唯一的方向。但是两张图中的LineVecs的方向有可能是不可靠的，图像有可能会有任意角度的旋转，对于这点，我们利用图像对之间存在的近似全局旋转角，可以减少候选匹配对的数目。

构建旋转

和其他文章中使用对应匹配来进行图像旋转不同，LBD的Matching中通过计算两个图像的LineVecs方向直方图，得到规范化直方图，h代表直方图。我们改变的角度，通过公式寻找一个全局近似旋转角。

而全局旋转变换不一定总是好的，所以我们也需要去检查估计旋转角是不是真的。实际上如果透视变换可以通过旋转来近似，那么直方图之差比较小。这代表了在进行了旋转之后，两个图像之间的相似程度。

上图就显示出了两张图之间的直方图差距，通过旋转我们可以得出两张图之间相似度很高。上图中的预估角度是0.349，偏移是0.243

但是如果图像中提取的线重复度很低的话，这种直方图方法就有可能提取出错误的旋转角度。为了解决这个问题，对于在方向直方图上落入相同区间bins的线段，将他们的长度累积起来。那么我们就可以得到一个长度向量，其第i个元素就是方向直方图中第i个bin中的线段累计长度。

我们设定最小偏移直方图小于阈值th，并且最小偏移长度向量距离小于阈值tl时，我们接受我们所估计的全局旋转角。一旦全局旋转角被接受，就会有一对LineVecs被匹配。但是如果这对LineVecs的方向角度和估计的全局旋转角之差超过阈值，那么我们认为他们是不能够匹配的。如果两个图片之间没有可以接受的旋转角度，那么我们只测试他们的外观相似性。

1.2. 局部外观相似性

我们用直线描述符之间的距离（lost）来度量局部外观相似度。
对于LineVec中的每个线段，我们都从提取出线的尺度层中生成一个LBD描述子向量V。当我们对一幅图像中提取出来的两组LineVec进行匹配，要去评估参考LineVec和测试LineVec中所有描述子之间的距离，并且用最小的描述子距离去测量LineVec外观相似度s。如果 s > ts s大于局部外观不相似容忍度，那么相应两个LineVecs将不会再进一步考虑。

在检查了LineVecs的一元几何属性和局部外观相似性之后，通过了这些测试的直线对被当做候选匹配。我们在上面的测试中，应当选取一组松散阈值，其中经验值是 tθ=π/4 ts=0.35。候选匹配的数量比实际匹配的数量要大很多，因为我们不能仅仅按照刚才两个属性来确定最终的匹配结果，当然我们上面的工作也是大大减小了图形匹配的问题维度的。

2. 构建关系图

对于上面得到一组候选匹配项，我们要构建一个关系图
其中关系图里的节点代表潜在的对应点
节点之间的连接的权重代表对应点之间的一致性。

拿到了k对对应关系，我们用一个大小为k*k的邻接矩阵A来表示关系图，其中第i行第j列的元素值是候选LineVec匹配对的一致性得分。其中分别是引用图和查询图的LineVecs变量，上面的一致性得分是通过候选匹配对的成对几何属性和外观相似度计算的来的。

成对几何属性

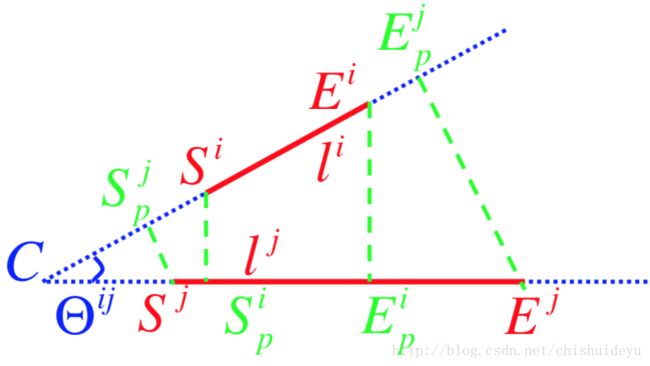
我们选择两条线分别是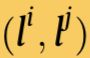，他们代表了这两个LineVecs之间的最小描述子距离，并在原图中定位他们的端点位置。然后我们用他们的交点比率，投影比率和相对角度来描述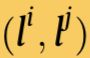的几何属性，就如上图所描述的那样。其中的两个值的计算方法如下：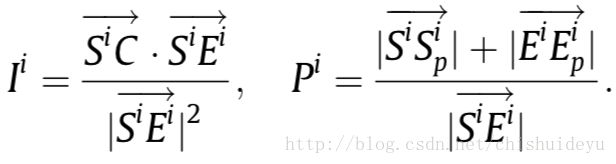

Ij和Pj的值可以用相同的方法求解得到，相对角度可以直接用线方向求得。这三个量对平移旋转缩放都是不变的。

外观相似度

之前，我们使用LBD描述向量来表示线的局部外观。
假设描述子与r图（参考图）和q图（查询图）的LineVecs之间的最小距离是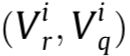，同理对是。我们可以得到两组成对几何属性和局部外观，分别是。

计算一致性得分Aij：

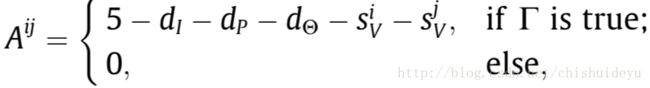
其中是几何相似性；是局部外观相似性；是条件。最后一个代表所有在内的元素都不能大于1。
接下来我们设。计算完他们的一致性得分之后，我们便获得了邻接矩阵A。

3. 生成最终匹配结果

到这一步之后，匹配的问题最终就变成了，寻找匹配簇LM，该匹配簇可以最大化总的一致性分数，以至于可以满足映射约束。我们使用一个指标向量来表示这个簇，否则为0，因此这个问题被表示为：

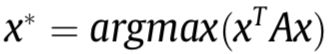
其中x受制于映射约束。一般来说用二次规划来解决这个问题太耗费资源，我们采用谱图技术，对x放款映射约束和积分约束，使得他的元素可以采集实际值在[0,1]区间里。
通过Raleigh比率定理，可以最大化的x*是A的主特征向量。它仍然是使用映射约束二值化特征向量和获得最优解的一个强大近似。

以下是算法细节：

1. 通过EDLine算法从参考图和查询图内提取LineVecs，以从两幅图中分别获得两组LineVecs
2. 利用两组LineVecs的方向直方图估计图像对的全局旋转角
3. 计算两组LineVecs的LBD描述子
4. 通过检查描述子的一元几何属性和局部外观，生成一组候选匹配对
5. 根据候选匹配对中一致性分数，构建k*k大小的邻接矩阵
6. 通过使用ARPACK库，得到邻接矩阵A的主特征向量x*
7. 初始化匹配结果
8. 查找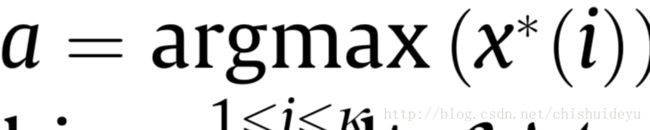，如果x*(a)=0，那么停止查找返回匹配结果LM，否则设，且x*(a)=0。
9. 检查CM中所有的候选者，如果和冲突，那么设
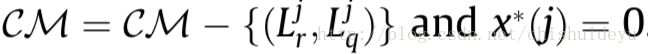
10. 如果CM是空的，那么返回LM，否则返回到步骤8。

最后一行的线段匹配可以从LineVecs LM的匹配结果直接检索。注意，在LineVec的线位于图像的同一区域，并且具有同一方向，因此，每对linevec的匹配，线段匹配有一对就足够检索了。

参考文档：
http://www.cnblogs.com/Jessica-jie/p/7545554.html

代码：
https://github.com/chishuideyu/LBD_and_LineMatching