强化学习系列（十）：On-policy Control with Approximation

一、前言

本章我们关注on-policy control 问题，这里采用参数化方法逼近action-value函数 q̂ (s,a,w)≈q(s,a) q ^ ( s , a , w ) ≈ q ( s , a ) ，其中， w w 为权重向量。在11章中会讨论off-policy方法。本章介绍了semi-gradient Sarsa算法，是对上一章中介绍的semi-gradient TD(0)的一种扩展，将其用于逼近action value, 并用于 on-policy control。在episodic 任务中，这种扩展是十分直观的，但对于连续问题来说，我们需要考虑如何将discount (折扣系数）用于定义optimal policy。值得注意的是，在对连续任务进行函数逼近时，我们必须放弃discount ，而改用一个新的形式 ” average reward”和一个“differential” value function进行表示。

首先，针对episodic任务，我们将上一章用于state value 的函数逼近思想扩展到action value上，然后我们将这些思想扩展到 on-policy GPI过程中，用 ϵ ϵ -greedy来选择action，最后针对连续任务，对包含differential value的average-reward运用上述思想。

二、Episode Semi-gradient Control

将第9章中的semi-gradient prediction 方法扩展到control问题中。这里，approximate action-value q̂ ≈qπ q ^ ≈ q π ，是权重向量 w w 的函数。在第9章中逼近state-value时，所采用的训练样例为 St↦Ut S t ↦ U t ，本章中所采用的训练样例为 St,At↦Ut S t , A t ↦ U t ，update target Ut U t 可以是 qπ(St,At) q π ( S t , A t ) 的任何逼近，无论是由MC还是n-step Sarsa获得。对action-value prediction 的梯度下降如下：

对one-step Sarsa而言，

我们将这种方法称为 Episode Semi-gradient one-step Sarsa，在policy不变的前提下，该方法和TD(0)的有同样的收敛边界条件：

为了构造control 问题，我们需要结合action-value prediction，policy improvement 和 action selection。目前还没有探索出十分适合连续动作空间或动作空间过大的问题的方法。另一方面，如果动作空间离散且不大的情况下，我们可以用之前章节中提到的方法。

因此，对当前state St S t 下，可能执行的action a，均计算出 q̂ (St,a,wt) q ^ ( S t , a , w t ) ，然后选择使得 q̂ (St,a,wt) q ^ ( S t , a , w t ) 最大的动作，即greedy action A∗t=argmaxaq̂ (St,a,wt) A t ∗ = a r g m a x a q ^ ( S t , a , w t ) 。Policy improvement，需要考虑探索问题，需要将被估计的policy变为 greedy policy 的 soft approximation，即 ϵ ϵ -greedy policy。同样，用 ϵ ϵ -greedy policy来选择action。算法伪代码如下：

三、n-step Semi-gradient Sarsa

通过令update target Ut=Gt:t+n U t = G t : t + n ,可以得到n-step semi-gradient Sarsa,其中 ：

此时的权重向量更新公式为：

算法伪代码如下：

四、Average Reward： A New Problem Setting for Continuing Tasks

为了构建马尔科夫过程（MDP）的求解目标，这里我们介绍除了 episodic setting 和discounted setting的第三种 setting—— average reward setting。

和discounted setting类似， average reward setting也是用于agent和环境不断交互，永不停止，没有开始或者没有结束的连续问题中。与discounted setting不同的是：没有折扣系数，agent对即刻reward 和延迟reward 的重视程度一致。 average reward setting主要出现在传统动态规划中，但很少出现在强化学习中。下一小节，我们将详细讨论对于函数逼近问题，discounted setting存在的问题。因此在解决连续任务下 函数逼近时，用 average reward setting代替 discounted setting。

在 average reward setting中，policy π π 的优劣由reward的平均率表示：

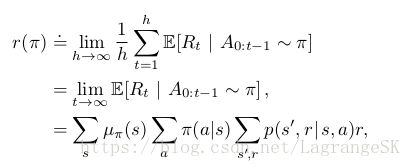
其中， μπ μ π 是稳态分布， μπ=limt→∞Pr{St=s|A0:t−1∼π} μ π = l i m t → ∞ P r { S t = s | A 0 : t − 1 ∼ π } ，假设 μπ μ π 对任意 π π 均存在，且独立于 S0 S 0 。这个假设对MDP来说被称为ergodicity (遍历）。这意味着MDP从何处开始或任何早期agent的决定所产生的影响都是暂时的。长期来说，一个state 下的期望值仅仅取决于policy和MDP状态转移概率。遍历条件是上式有极值的重要保证。

对undiscounted连续问题来说，很难区分哪种优化方法好，但根据每个time step的average reward规划出policy比较实用。也就是通过求解 r(π) r ( π ) ，计算出使得 r(π) r ( π ) 最大的 π π 作为optimal Policy。

稳态分布是一种特殊分布，如果根据policy π π 选择了一个action，分布仍然不改变，因此有：

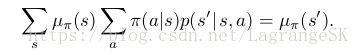
在average reward setting中，return和之前定义的也不同，由reward和average reward 的差值组成：

被叫做 differential return，对应的value function 是 differential value function。differential value function和之前定义的value function使用相同的符号： vπ(s)=Eπ[Gt|St=s] v π ( s ) = E π [ G t | S t = s ] , qπ(s,a)=Eπ[Gt|St=s,At=a] q π ( s , a ) = E π [ G t | S t = s , A t = a ] （另外还有 v∗ v ∗ 和 q∗ q ∗ )。同样也满足Bellman等式：

也有两种形式的TD error:

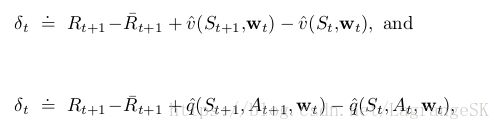
其中， R⎯⎯⎯⎯t R ¯ t 表示 t时刻 average reward r(π) r ( π ) 的估计值，这样很多算法可以直接用于average reward setting。

举个例子，semi-gradient Sarsa 的 average reward版本的权重更新公式为：

其中， δt=Rt+1−R⎯⎯⎯⎯t+1+q̂ (St+1,At+1,wt)−q̂ (St,At,wt) δ t = R t + 1 − R ¯ t + 1 + q ^ ( S t + 1 , A t + 1 , w t ) − q ^ ( S t , A t , w t ) ,算法伪代码如下：

五、Deprecating the Discounted Setting

上一节提到，在连续函数逼近任务中，我们用average reward setting来取代discounted setting，但没有说明原因，本节重点讨论为什么要这么做。

首先，考虑一个无限长的return 序列，没有起点或终点，也没有关于states 的明确定义，state可以用特征向量表示，但相互之间没啥区分度。当所有特征向量都一样的特殊情况，只有一个reward序列（和一个action序列），Policy 性能如何由这些量估计？一种方式是在长区间内求解reward的平均值，这是average reward setting 的思想。如果要用到discount 呢？每一个time step都需要构造一个discounted return,一些大一些小，对足够长的时间区间的return 求平均值。

在没有起点也没有终点的连续问题中，没有time step的概念。如果你用了discount ，那么可以证明discounted returns 与 average reward成比例。事实上，对某个策略 π π ，discounted returns的平均为 r(π)/(1−γ) r ( π ) / ( 1 − γ ) ，其中 r(π) r ( π ) 是average reward。按照这两种方式所选出的Policy的顺序一致，折扣系数 γ γ 对结果没有影响。

下面详细证明了这一理论：

这说明了用 on-policy distribution 来优化 discounted value 和优化 undiscounted average reward结果相同，折扣系数 γ γ 对结果没有影响。

另外，在函数逼近中使用 discounted control setting有困难的根本原因在于不能满足第四章中的policy improvement 理论。如果我们按照提升discounted value来改变policy，则不能保证policy 一定会被提升。但这个策略提升理论是强化学习control 方法的关键，使用了函数逼近使得我们失去了这一保证。

事实上，policy improvement 理论缺失也发生在total-episodic和average-reward setting 的函数逼近中。一旦我们开始进行函数逼近，我们将不能保证Policy improvement。在13章中，我们介绍一种非传统类型的强化学习算法，基于参数化的policy，然后运用“Policy Gradient theorem”取代policy improvement理论，以达到策略提升的目的。但对目前这种学习 action value 的方式，还没有policy improvement的理论保证。

六、n-step Differential Semi-gradient Sarsa

为了泛化 n-step bootstrapping方法，我们需要n-step TD error。首先我们用average-reward setting 方式定义 n-step return:

此时，n-step TD error 为：

算法伪代码如下：

七、总结

本章我们将第九章中参数化函数逼近和semi-gradient decent 扩展到control 问题在中。首先，对episodic问题进行了简单扩展，然后对连续问题，先介绍了average-reward setting 和 differential value function。然后说明了discounted setting 不适用于连续问题中的函数逼近的原因。

average reward中的 differential value function也有Bellman等式、TD error。我们用他们构造了differential version of semi-gradient n-step Sarsa。

Reinforcement Learning: an introduction