SPSS(一)进行单因素方差分析及多重比较检验(图文教程)
spss教程进行单因素方差分析(图文教程)
单因素方差分析原理
因变量:连续变量
自变量:多分类
用来测试某一个控制变量的不同水平是否给观察变量造成显著差异和变动。
方差分析前提:不同水平下,各总体均值服从方差相同的正态分布。所以方差分析就是研究不同水平下各个总体的均值是否有显著的差异。统计推断方法是计算F统计量,进行F检验,总的变异平方和 SST,控制变量引起的离差SSA(Between Group离差平方和),另一部分随机变量引起的SSE(组内Within Group离差平方和),SST=SSA+SSE。
简单来说:数据具有独立性(主要看数据背景)、数据要符合正态性(直方图、P-P图、Q-Q图)、不同水平的方差齐性等不等
计算检验统计量的观察值和概率P值:Spss自动计算F统计值,如果相伴概率P小于显著性水平a(一般取0.05),拒绝零假设,认为控制变量不同水平下各总体均值有显著差异,反之,则相反,即没有差异。
spss实现单因素方差分析
现希望比较四种胶合板的耐磨性,分别从这四个品牌的胶合板中抽取了5个样品,在相同的转速下磨损相同时间,测量其被磨损的深度(mm),现希望对此进行分析
首先检验数据源是否适用单因素方差分析
- 数据符合独立性
- 由于数据量偏少,不符合正态也可以理解
- 方差齐性检验:控制变量不同水平下各观察变量总体方差是否相等进行分析。采用方差同质性检验方法(Homogeneity of variance),原假设“各水平下观察变量总体的方差无显著差异,思路同spss两独立样本t检验中的方差分析”。 图中相伴概率0.515大于显著性水平0.05,故认为总体方差相等。
数据集如下
2.30 A
2.32 A
2.40 A
2.45 A
2.58 A
2.35 B
2.30 B
2.42 B
2.60 B
2.35 B
2.20 C
2.00 C
1.90 C
2.10 C
2.03 C
2.54 D
2.61 D
2.60 D
2.57 D
2.54 D
由于单因素自变量要求是数值型变量,数据不满足模型要求,先进行自动重新编码
我们接下来进行方差齐性检验和单因素方差分析,这两个步骤可以并行一行弄得,SPSS有提供相关方法
(分析--比较均值--单因素ANOVA)
对比下面的方差同质性检验方法就是检验方差齐性的
之后点击确定
结果显著性0.311大于显著性水平0.05,所以各水平满足方差齐性
单因素方差分析显著性P=0小于显著性水平a=0.05,拒绝零假设,认为控制变量不同水平下各总体均值有显著差异
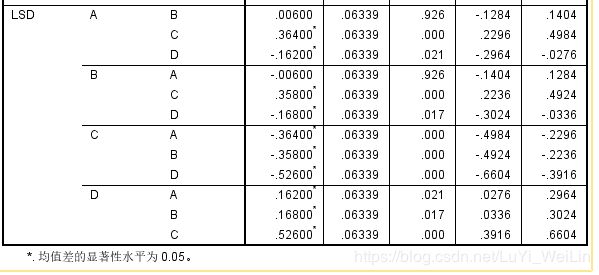
多重比较检验(拒绝了原假设,这一步才有意义)
假如不同水平下各总体均值有显著差异可继续进行这一步
多重比较检验:单因素方差分析只能够判断控制变量是否对观察变量产生了显著影响,多重比较检验可以进一步确定控制变量的不同水平对观察变量的影响程度如何,那个水平显著,哪个不显著。
(分析--比较均值--单因素ANOVA)
两两比较方法
- LSD法:实际上就是t检验的变形,只是在变异和自由度的计算上利用了整个样本信息,因此仍然存在放大一类错误的问题
- Scheffe法:当各组人数不相等,或者想进行复杂的比较时,用此法较为稳妥。但它相对比较保守
- S-N-K法:是运用最广泛的一种两两比较方法。它采用Student Range 分布进行所有各组均值间的配对比较。该方法保证在H0真正成立时总的α水准等于实际设定值,即控制了一类错误
- Tukey法对一、二类问题控制得很好,首选
- Bonferroni法:LSD法的改进,有效控制假阳性(第一类错误)
什么是证实性研究呢?
研究者都有明确的研究目的和具体的研究假设,已经事先定义好谁和谁比较了,而不是探索性研究,也就是所有自变量全部对比一遍
点击确定,得到结果
方差不齐有什么矫正的方法吗?
方差分析对各组方差的方差齐性(也就是各组方差是否一致)有要求,如果方差不齐,你不能使用方差分析。不过,SPSS统计软件的one way ANOVA在方差不齐时是可以使用的,此时你应该使用Brown-Forsythe或Welch的修正值。当你想看哪两组有差异时,可以使用one way ANOVA自带的Post Hoc Tests,方差不齐时使用不等方差假设项下的Tamhane's T2或Dunnett's T3等。
方差不齐时的两两比较方法
一般认为是Games-Howell法稍好一些,但最好直接使用非参数检验方法
相似性子集
相似性子集:由图可知,划分的子集结果是一样的。通常在相似性子集划分时多采用S-N-K方法的结论。其结论可以与上述多重比较检验结合起来看,验证在LSD项中,A与B没有显著差异的结论。
当然也会我们也会看到下面方法可以看出使用不同方法得到划分相似性子集不一样,是因为各个数学家使用的方法原理不一样所以得到不一样的结果
我们还可以看单因素方差分析的参数估计和对比系数矩阵(分析----一般线性模型----选项)
参数估计要结合对比系数矩阵来查看,上图框红框证明是第一个和第四个做比较
参数估计中brandnew4为0,证明以第四个品牌为参考水平均值,其均值就等于截距2.572
brandnew1为-0.162,所以brandnew1的均值为水平均值-0.162=2.572-0.162