WEBRTC中VAD算法及思想的数学解析
版权声明:本文为博主原创文章,未经博主允许不得转载。
0 概述
VAD(Voice Activity Detection), 活动语音检测技术在语音信号处理有着重要的作用,如语音增强中估计噪声、语音识别中进行语音端点检测,在语音信号传输中用于非连续传输等等。
本文全面解析WEBRTC 中VAD 算法,该算法主要原理是将信号在频谱上进行子带划分为 80~ 250Hz,250~ 500Hz,500Hz~ 1K, 1~ 2K,2~ 3K,3~4KHz ,6个频带,计算每个频带能量为特征;通过假设检验,构建了噪声和语音两个假设,从而对每个子带构建由2个高斯分布组合的噪声和语音的混合高斯分布模型。通过极大似然估计对模型进行自适应学习优化,并通过概率比判决推断。
该算法重点涉及了子带划分技术、极大似然估计、假设检验等知识,本文将通过信号与系统、统计学习的知识解析代码中所蕴含的数学。
1 子带划分滤波器 SplitFilter
1.1 全通滤波器 AllPassFilter

从函数中
tmp32 = state32 + filter_coefficient * *data_in;
state32 = (*data_in * (1 << 14)) - filter_coefficient * tmp16;
令 x ( n ) x(n) x(n)为输入序列, y ( n ) y(n) y(n)为输出序列, c c c为实系数filter_coefficient ,可知表示 :
y ( n ) = x ( n − 1 ) − c ∗ y ( n − 1 ) + c ∗ x ( n ) y(n) =x(n-1)-c*y(n-1) + c*x(n) y(n)=x(n−1)−c∗y(n−1)+c∗x(n)
但由于函数中data_in +=2, 即反馈是只与历史第二值相关的,其表示为:
y ( n ) = x ( n − 2 ) − c ∗ y ( n − 2 ) + c ∗ x ( n ) y(n) =x(n-2)-c*y(n-2) + c*x(n) y(n)=x(n−2)−c∗y(n−2)+c∗x(n)
则传输函数为:
H ( z ) = c + z − 2 1 + c z − 2 H(z) = \frac{c+z^{-2}}{1+cz^{-2}} H(z)=1+cz−2c+z−2
是一个2阶全通滤波器, ∣ H ( w ) ∣ = 1 |H(w)| = 1 ∣H(w)∣=1。
1.2 IIR 传输函数的并联全通实现
根据IIR传输函数通过全通函数并联性质【参考文献《数字信号处理–基于计算机的方法》】:
-
一对互补的低通和高通传输函数可有两个稳定的全通滤波器并联组成:
F ( z ) = 1 2 ( A 0 ( z ) + A 1 ( z ) ) F(z)= \frac{1}{2}(A_0(z)+A_1(z)) F(z)=21(A0(z)+A1(z)) G ( z ) = 1 2 ( A 0 ( z ) − A 1 ( z ) ) G(z)= \frac{1}{2}(A_0(z)-A_1(z)) G(z)=21(A0(z)−A1(z)) ∣ F ( z ) ∣ 2 + ∣ G ( z ) ∣ 2 = 1 |F(z)|^2 + |G(z)|^2 = 1 ∣F(z)∣2+∣G(z)∣2=1 -
对于低通高通滤波器对,传输函数的阶数N必须是奇数,其中 A 0 ( z ) A_0(z) A0(z)和 A 1 ( z ) A_1(z) A1(z)的阶数相差1。
由上述可知,一对互补的低通高通传输函数可以有两个相同阶数的全通函数多相分解得出:
E ( z ) = E 0 ( z 2 ) + z − 1 E 1 ( z 2 ) E(z) = E_0(z^2) + z^{-1}E_1(z^2) E(z)=E0(z2)+z−1E1(z2)
E 0 ( z 2 ) E_0(z^2) E0(z2)和 E 1 ( z 2 ) E_1(z^2) E1(z2)为相同阶数的全通函数, z − 1 z^{-1} z−1使输入序列移位。

webrtc vad 中SplitFilter 正是通过上述IIR传输函数多相分解成全通函数并联技术实现,并实现对输出2倍下抽样。
第一个全通滤波器的参数kAllPassCoefsQ15[0] = 20972, 即 c = 20972 / ( 2 15 ) = 0.64 c=20972/(2^{15})=0.64 c=20972/(215)=0.64,则传输函数:
A 0 ( z ) = 0.64 + z − 2 1 + 0.64 ∗ z − 2 A_0(z) = \frac{0.64+z^{-2}}{1+0.64*z^{-2}} A0(z)=1+0.64∗z−20.64+z−2
第二个全通滤波器的参数kAllPassCoefsQ15[0] = 5571, 即 c = 5571 / ( 2 15 ) = 0.17 c=5571/(2^{15})=0.17 c=5571/(215)=0.17, 则传输函数:
A 1 ( z ) = 0.17 + z − 2 1 + 0.17 ∗ z − 2 A_1(z) = \frac{0.17+z^{-2}}{1+0.17*z^{-2}} A1(z)=1+0.17∗z−20.17+z−2
第一个全通滤波器的输入序列data_in[n]是第二个全通函数输入序列data_in[n+1]的移位,且全通滤波器中输出是 tmp16 = (int16_t) (tmp32 >> 16); // Q(-1) *data_out++ = tmp16;Q(-1), 即 1 / 2 1/2 1/2的输出,则传输函数为
H ( z ) = 1 2 ( A 1 ( z ) − + z − 1 A 0 ( z ) ) H(z)= \frac{1}{2}(A_1(z) _-^+ z^{-1}A_0(z)) H(z)=21(A1(z)−+z−1A0(z))
由于全通函数的输出只与当前输入值和历史第二输入值、输出值有关,而全通滤波器的当前输入是2倍下抽样输入x(2n+1),即data_in[1]、data_in[3]、data_in[5]……,则输出也只计算得到data_out[1]、data_out[3]、data_out[5]……, 相当于对原输出y(n)进行2倍下抽样的数据y(2n+1)。
函数中*hp_data_out++ -= *lp_data_out;对应的高通传输函数:
H h i g h = 1 2 ( A 1 ( z ) − z − 1 A 0 ( z ) ) H_{high} =\frac{1}{2}(A_1(z) - z^{-1}A_0(z)) Hhigh=21(A1(z)−z−1A0(z)) H h i g h = 1 2 ( 0.17 + z − 2 1 + 0.17 ∗ z − 2 − z − 1 0.64 + z − 2 1 + 0.64 ∗ z − 2 ) H_{high} =\frac{1}{2}( \frac{0.17+z^{-2}}{1+0.17*z^{-2}} - z^{-1}\frac{0.64+z^{-2}}{1+0.64*z^{-2}}) Hhigh=21(1+0.17∗z−20.17+z−2−z−11+0.64∗z−20.64+z−2)
函数中*lp_data_out++ += tmp_out;对应的低通传输函数:
H l o w = 1 2 ( A 1 ( z ) + z − 1 A 0 ( z ) ) H_{low} =\frac{1}{2}(A_1(z) + z^{-1}A_0(z)) Hlow=21(A1(z)+z−1A0(z)) H l o w = 1 2 ( 0.17 + z − 2 1 + 0.17 ∗ z − 2 + z − 1 0.64 + z − 2 1 + 0.64 ∗ z − 2 ) H_{low} =\frac{1}{2}( \frac{0.17+z^{-2}}{1+0.17*z^{-2}} + z^{-1}\frac{0.64+z^{-2}}{1+0.64*z^{-2}}) Hlow=21(1+0.17∗z−20.17+z−2+z−11+0.64∗z−20.64+z−2)
通过matlab画出上述低通滤波器和高通滤波器:
%sliptfilter
clc; close all; clear all;
%20972 5571
% 全通滤波器 z^-1* A1(z)
c = 20972/(2^15);
B =[0 c 0 1];
A =[1 0 c];
[A1,W1] = freqz(B,A,1024,'whole',4000);
A1f =abs(A1);
A1a = angle(A1);
x = 4000/512;
%plot((1:512)*x,A1f(1:512));
% 全通滤波器 A0(z)
c = 5571/(2^15);
B =[c 0 1];
A =[1 0 c];
[A0,W0] = freqz(B,A,1024,'whole',4000);
A0f =abs(A0);
A0a = angle(A0);
%plot((1:512)*x,A0f(1:512));
% 高通滤波
H = A1 - A0;
H = H/2;
Hf=abs(H);
Ha= angle(H);
plot((1:512)*x,Hf(1:512)); hold on;
%低通滤波
L = A1 + A0;
L = L/2;
Lf = abs(L);
La = angle(L);
plot((1:512)*x,Lf(1:512));
2 高斯正态分布(Gaussian normal distribution)概率的数值计算
高斯正太分布的概率计算公式为:
1 2 π s ∗ e − ( x − m ) 2 2 ∗ s 2 \frac{1}{ \sqrt{2\pi}s} * e^{ \frac{-(x - m)^2} {2 * s^2} } 2πs1∗e2∗s2−(x−m)2
WebRtcVad_GaussianProbability 正是用于计算上述概率值的函数,该函数采用巧妙计算机数值计算,近似地求解浮点指数下的概率值。
由于之后求解是求解似然比,因此该函数不考虑计算尺度 1 2 π \frac{1}{ \sqrt{2\pi}} 2π1 。
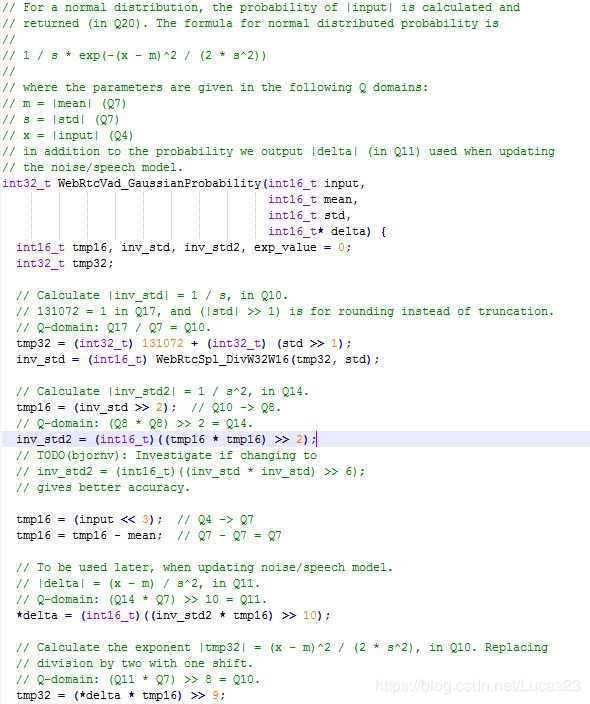
// Calculate |inv_std| = 1 / s, in Q10.
// 131072 = 1 in Q17, and (|std| >> 1) is for rounding instead of truncation.
// Q-domain: Q17 / Q7 = Q10.
tmp32 = (int32_t) 131072 + (int32_t) (std >> 1);
inv_std = (int16_t) WebRtcSpl_DivW32W16(tmp32, std);
首先上面代码求方差倒数 1 / s 1/s 1/s,其做法是对小数进行四舍五入(rounding)而不是直接截断(truncation), 所以加了(std >> 1), 即在Q7的std的一半,也就是0.5(小数部分加0.5 强转整形下截断就得四舍五入结果)。
接下来计算得到式子|tmp32| = (x - m)^2 / (2 * s^2), in Q10.,当tmp32 < kCompVar时(如果大于,则趋于0)求它的 e e e自然指数解,这里通过计算机数值计算巧妙近似求解。
// If the exponent is small enough to give a non-zero probability we calculate
// |exp_value| ~= exp(-(x - m)^2 / (2 * s^2))
// ~= exp2(-log2(exp(1)) * |tmp32|).
if (tmp32 < kCompVar) {
// Calculate |tmp16| = log2(exp(1)) * |tmp32|, in Q10.
// Q-domain: (Q12 * Q10) >> 12 = Q10.
tmp16 = (int16_t)((kLog2Exp * tmp32) >> 12);
tmp16 = -tmp16;
exp_value = (0x0400 | (tmp16 & 0x03FF));
tmp16 ^= 0xFFFF;
tmp16 >>= 10;
tmp16 += 1;
// Get |exp_value| = exp(-|tmp32|) in Q10.
exp_value >>= tmp16;
}
上面自然指数函数:
e − ( x − m ) 2 2 ∗ s 2 e^{ \frac{-(x - m)^2} {2 * s^2} } e2∗s2−(x−m)2
可以通过换为2的指数函数(代码中exp2是2指数: 2 x 2^x 2x)化为:
2 − l o g 2 e ∗ ( x − m ) 2 2 ∗ s 2 2^{-log_2 e*{ \frac{(x - m)^2} {2 * s^2}}} 2−log2e∗2∗s2(x−m)2
// Q-domain: (Q12 * Q10) >> 12 = Q10.
tmp16 = (int16_t)((kLog2Exp * tmp32) >> 12);
tmp16 = -tmp16;
上面得到tmp16为 − l o g 2 e ∗ ( x − m ) 2 2 ∗ s 2 -log_2 e*{ \frac{(x - m)^2} {2 * s^2}} −log2e∗2∗s2(x−m)2, 是一个负的Q10值。
exp_value = (0x0400 | (tmp16 & 0x03FF));
将tmp16 与 0x03FF按位与操作,取低10位,即Q10的小数部分记 f f f,由于tmp16是个负值,机器码为反码表示,那么得与的结果记为 f i n v = 1 − f f_{inv} = 1-f finv=1−f, 比如tmp16为-3.6(Q0), 那么tmp16 & 0x03FF为0.4(Q0)。那么再或上0x0400,exp_value在Q0就是一个1.x的值:
e x p _ v a l u e = 1 + f i n v exp\_value = 1+ f_{inv} exp_value=1+finv
tmp16 ^= 0xFFFF;
tmp16 >>= 10;
tmp16 += 1;
接着,tmp16 异或0xFFFF, 即求反码,由于tmp16 是个负值,机器码求反码就变其绝对值(这里应该是求补码,即反码再加1,但这里省略近似,因为Q10的1 很是很小值)。接下来tmp16 >>= 10转为Q0的实数部分记为 r r r, 那么原来
2 − l o g 2 e ∗ ( x − m ) 2 2 ∗ s 2 2^{-log_2 e*{ \frac{(x - m)^2} {2 * s^2}}} 2−log2e∗2∗s2(x−m)2
便可记为:
2 − c , c 为 实 数 部 分 r 和 小 数 f 组 成 的 值 , 即 c = r + f 2^{-c}, c为实数部分r 和小数f 组成的值,即c=r+f 2−c,c为实数部分r和小数f组成的值,即c=r+f
= 2 − ( r + f ) = 2 − ( r + 1 ) 2 1 − f = 2 − ( r + 1 ) 2 f i n v = 2^{-(r+f)}= 2^{-(r+1)}2^{1-f}= 2^{-(r+1)}2^{f_{inv}} =2−(r+f)=2−(r+1)21−f=2−(r+1)2finv
r + 1 r+1 r+1便是tmp16 += 1这时候的tmp16值,即 t m p 16 = r + 1 tmp16= r+1 tmp16=r+1,。
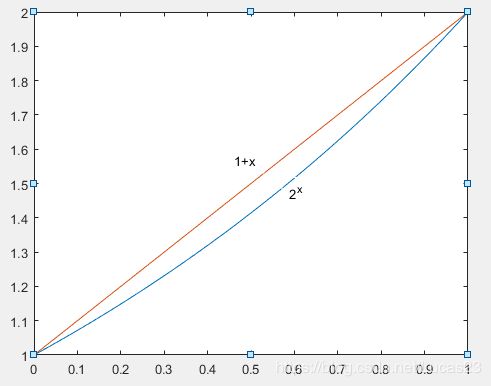
这里利用近似解:
2 f i n v ≈ 1 + f i n v 2^{f_{inv}} \approx 1+f_{inv} 2finv≈1+finv
通过matlab画图:
clc; clear all; close all;
x = (0:0.01:1);
y = 2.^x;
z = 1 + x;
plot(x,y ,x, z);
// Get |exp_value| = exp(-|tmp32|) in Q10.
exp_value >>= tmp16;
看上面最终代码,以及 t m p 16 = r + 1 tmp16 = r+1 tmp16=r+1、 e x p _ v a l u e = 1 + f i n v exp\_value = 1+ f_{inv} exp_value=1+finv, 所以
2 − l o g 2 e ∗ ( x − m ) 2 2 ∗ s 2 2^{-log_2 e*{ \frac{(x - m)^2} {2 * s^2}}} 2−log2e∗2∗s2(x−m)2 = 2 − ( r + 1 ) 2 f i n v =2^{-(r+1)}2^{f_{inv}} =2−(r+1)2finv ≈ 2 − ( r + 1 ) ( 1 + f i n v ) = 2 − ( r + 1 ) ∗ e x p _ v a l u e \approx 2^{-(r+1)}(1+ f_{inv})=2^{-(r+1)}*exp\_value ≈2−(r+1)(1+finv)=2−(r+1)∗exp_value = e x p _ v a l u e > > t m p 16 = exp\_value >> tmp16 =exp_value>>tmp16
// Calculate and return (1 / s) * exp(-(x - m)^2 / (2 * s^2)), in Q20.
// Q-domain: Q10 * Q10 = Q20.
return inv_std * exp_value;
exp_value与inv_std相乘,最终返回当前概率值。
3 基于假设的似然检验(LRT with hypothesis)
3.1 计算似然概率及判决
每一个频带的特征所对应是由两个高斯分布组合的高斯混合模型(这里不讲解高斯混合模型,比较基础,无非就是仅一个高斯分布不足以表示数据的真正分布情况,所以用多个加权组合来拟合)。
判决的方法就是计算每一个频带特征分别在噪声概率分布假设和语音概率分布假设的似然概率Pr{X|H0} Pr{X|H1}的比值来来判断:当其中某一子频带的似然比满足阈值或者整体频道似然比满足阈值则判决为语音,如下代码:

![]()
但代码中直接用似然概率表达并不准确,因为X在H0发生的可能性大,可能是因为H0发生的可能性大,即先验概率Pr{H0} Pr{H1}无法比较。
对于统计分类判决,该特征样本发生后属于哪个类别是其后验概率,即Pr{H0|X} Pr{H1|X}, 也即最大后验概率准则的判决。通过贝叶斯定理:
p ( x ∣ H ) = p ( H ∣ x ) p ( x ) p ( H ) p(x|H) = \frac{p(H|x)p(x)}{p(H)} p(x∣H)=p(H)p(H∣x)p(x)
由此可见,代码直接使用似然概率是假设了噪声和语音的先验概率一样,即在一段音频数据大概一半是噪声一半有语音。
3.2 极大似然估计更新参数
对模型的参数更新,这里使用极大似然估计的方法。所谓极大似然简单地说就是当样本出现的这个事件时,认为该样本具有最大的概率,那么希望概率分布的参数使得该样概率最大:
L ( θ ; x 1 、 x 2 … … x n ) = ∏ p ( x k ; θ ) L(\theta; x_1、x_2……x_n) = \prod{p(x_k;\theta )} L(θ;x1、x2……xn)=∏p(xk;θ)
上面假设了样本独立发生,假设有 θ ^ \hat{\theta} θ^使得 L ( θ , x 1 、 x 2 … … x n ) L(\theta, x_1、x_2……x_n) L(θ,x1、x2……xn)最大,那么 θ ^ \hat{\theta} θ^是参数 θ \theta θ的极大似然估计值。
这里每次发生的样本的只有一个,即通过3.1节的特征样本经过上一次的模型概率分布判决事件,由于该模型为高斯混合模型,其极大似然函数可设计为:
L ( θ ) = p ( G 0 ) ∗ l o g G 0 ( x ; θ 0 ) + p ( G 1 ) ∗ l o g G 1 ( x ; θ 1 ) L(\theta) = p(G_0)*logG_0(x;\theta_0)+p(G_1)*logG_1(x;\theta_1) L(θ)=p(G0)∗logG0(x;θ0)+p(G1)∗logG1(x;θ1)
上式中, θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1分别代表各自高斯函数参数,如 μ 0 、 σ 0 , μ 1 、 σ 1 \mu_0、\sigma_0,\mu_1、\sigma_1 μ0、σ0,μ1、σ1; θ \theta θ为其中某一参数,对其更新便是在样本 x x x出现,并被判决为某个结果(噪声或语音)时,求得 θ ^ \hat{\theta} θ^ 使得 L ( θ ) L(\theta) L(θ)极大。 p ( G k ) p(G_k) p(Gk)为对应高斯分布的权重。其取对数是计算似然的常用技术,对数函数是单调性,保持原来函数的极值位置和函数值的大小关系,可以化简指数函数,可以将乘除变为加减,大大简化计算,这里 l o g log log表示取对数,显然高斯分布是自然指数,所以为 e e e为底的 l n ln ln。
由于每次更新只有一个样本特征,得到当前的似然极大估计并不准确(过拟合),希望在每次更新步进朝极大值更新,这里使用梯度下降法来迭代实现最优化:
θ ^ = θ − c ∗ ∇ ( L ( θ ) ) \hat\theta = \theta - c*\nabla(L(\theta)) θ^=θ−c∗∇(L(θ))
由于梯度下降法是对具有极小值的代价函数(误差函数)的优化,我们这是有极大值的分布函数,故这里是梯度提升:
θ ^ = θ + c ∗ ∇ ( L ( θ ) ) \hat\theta = \theta+c*\nabla(L(\theta)) θ^=θ+c∗∇(L(θ))
上式 ∇ ( L ( θ ) ) \nabla(L(\theta)) ∇(L(θ)) 是 L L L 在 θ \theta θ梯度, c c c为步进因子,该值较小时更新到最优的速度较慢,该值较大时可能不能得到极值,而是在极值附近振荡。
3.2.1 高斯分布均值更新
现在我们来求第一个高斯模型均值参数 u 0 u_0 u0的更新:
L ( u 0 ) = p ( G 0 ) ∗ l o g G 0 ( x ; u 0 ) + p ( G 1 ) ∗ l o g G 1 ( x ; θ 1 ) L(u_0) = p(G_0)*logG_0(x;u_0)+p(G_1)*logG_1(x;\theta_1) L(u0)=p(G0)∗logG0(x;u0)+p(G1)∗logG1(x;θ1)
上式对 u 0 u_0 u0 求导, p ( G 1 ) ∗ l o g G 1 ( x ; θ 1 ) p(G_1)*logG_1(x;\theta_1) p(G1)∗logG1(x;θ1) 该项与 u 0 u_0 u0无关,导数为0,故忽略。则
p ( G 0 ) ∗ l o g G 0 ( x ; u 0 ) p(G_0)*logG_0(x;u_0) p(G0)∗logG0(x;u0) = p ( G 0 ) ∗ l o g 1 2 π σ 0 ∗ e − ( x − u 0 ) 2 2 ∗ σ 0 2 =p(G_0)*log\frac{1}{ \sqrt{2\pi}\sigma_0} * e^{ \frac{-(x - u_0)^2} {2 * \sigma_0^2} } =p(G0)∗log2πσ01∗e2∗σ02−(x−u0)2 = p ( G 0 ) ∗ l o g 1 2 π σ 0 + p ( G 0 ) ∗ l o g e − ( x − u 0 ) 2 2 ∗ σ 0 2 =p(G_0)*log\frac{1}{ \sqrt{2\pi}\sigma_0} + p(G_0)*loge^{ \frac{-(x - u_0)^2} {2 * \sigma_0^2} } =p(G0)∗log2πσ01+p(G0)∗loge2∗σ02−(x−u0)2 = p ( G 0 ) ∗ l o g 1 2 π σ 0 + p ( G 0 ) ∗ − ( x − u 0 ) 2 2 ∗ σ 0 2 =p(G_0)*log\frac{1}{ \sqrt{2\pi}\sigma_0} + p(G_0)*\frac{-(x - u_0)^2} {2 * \sigma_0^2} =p(G0)∗log2πσ01+p(G0)∗2∗σ02−(x−u0)2
上式继续忽略与 u 0 u_0 u0无关项,则
∇ ( L ( u 0 ) ) = ∇ ( p ( G 0 ) ∗ − ( x − u 0 ) 2 2 ∗ σ 0 2 ) \nabla(L(u_0)) = \nabla(p(G_0)*\frac{-(x - u_0)^2} {2 * \sigma_0^2} ) ∇(L(u0))=∇(p(G0)∗2∗σ02−(x−u0)2) = p ( G 0 ) ∗ x − u 0 σ 0 2 =p(G_0)*\frac{x-u_0}{\sigma_0^2} =p(G0)∗σ02x−u0
则 u 0 u_0 u0的更新:
u ^ 0 = u 0 + p ( G 0 ) ∗ x − u 0 σ 0 2 ∗ c \hat u_0 = u_0 + p(G_0)*\frac{x-u_0}{\sigma_0^2}*c u^0=u0+p(G0)∗σ02x−u0∗c
同理,对第二高斯分布以及语音的两个高斯分布的均值更新的一般函数为:
u ^ = u + p ( G ) ∗ x − u σ 2 ∗ c \hat u = u + p(G)*\frac{x-u}{\sigma^2}*c u^=u+p(G)∗σ2x−u∗c
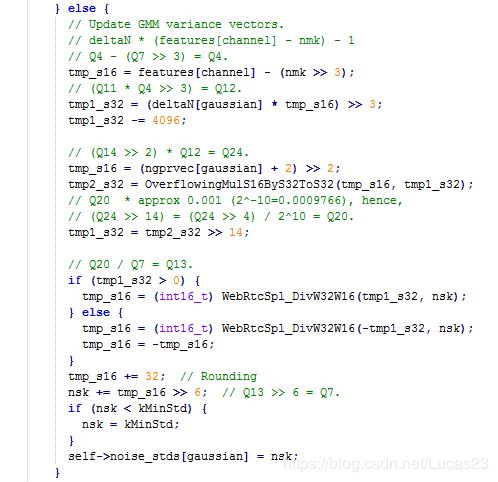
3.2.2 高斯分布方差更新
接下来我们来求第一个高斯模型方差参数 σ 0 \sigma_0 σ0的更新:
L ( σ 0 ) = p ( G 0 ) ∗ l o g G 0 ( x ; σ 0 ) + p ( G 1 ) ∗ l o g G 1 ( x ; θ 1 ) L(\sigma_0) = p(G_0)*logG_0(x;\sigma_0)+p(G_1)*logG_1(x;\theta_1) L(σ0)=p(G0)∗logG0(x;σ0)+p(G1)∗logG1(x;θ1)
上式对 σ 0 \sigma_0 σ0 求导, p ( G 1 ) ∗ l o g G 1 ( x ; θ 1 ) p(G_1)*logG_1(x;\theta_1) p(G1)∗logG1(x;θ1) 该项与 σ 0 \sigma_0 σ0无关,导数为0,故忽略。则
p ( G 0 ) ∗ l o g G 0 ( x ; σ 0 ) p(G_0)*logG_0(x;\sigma_0) p(G0)∗logG0(x;σ0) = p ( G 0 ) ∗ l o g 1 2 π σ 0 ∗ e − ( x − u 0 ) 2 2 ∗ σ 0 2 =p(G_0)*log\frac{1}{ \sqrt{2\pi}\sigma_0} * e^{ \frac{-(x - u_0)^2} {2 * \sigma_0^2} } =p(G0)∗log2πσ01∗e2∗σ02−(x−u0)2 = p ( G 0 ) ∗ l o g 1 2 π σ 0 + p ( G 0 ) ∗ l o g e − ( x − u 0 ) 2 2 ∗ σ 0 2 =p(G_0)*log\frac{1}{ \sqrt{2\pi}\sigma_0} + p(G_0)*loge^{ \frac{-(x - u_0)^2} {2 * \sigma_0^2} } =p(G0)∗log2πσ01+p(G0)∗loge2∗σ02−(x−u0)2 = p ( G 0 ) ∗ l o g 1 2 π + p ( G 0 ) ∗ l o g 1 σ 0 + p ( G 0 ) ∗ − ( x − u 0 ) 2 2 ∗ σ 0 2 =p(G_0)*log\frac{1}{ \sqrt{2\pi}} + p(G_0)*log\frac{1}{\sigma_0}+ p(G_0)*\frac{-(x - u_0)^2} {2 * \sigma_0^2} =p(G0)∗log2π1+p(G0)∗logσ01+p(G0)∗2∗σ02−(x−u0)2
上式继续忽略与 σ 0 \sigma_0 σ0无关项,则
∇ ( L ( u 0 ) ) = p ( G 0 ) ∗ ∇ ( l o g 1 σ 0 + − ( x − u 0 ) 2 2 ∗ σ 0 2 ) \nabla(L(u_0)) = p(G_0)*\nabla(log\frac{1}{\sigma_0} + \frac{-(x - u_0)^2} {2 * \sigma_0^2} ) ∇(L(u0))=p(G0)∗∇(logσ01+2∗σ02−(x−u0)2) = p ( G 0 ) ∗ ( − 1 σ 0 + ( x − u 0 ) 2 σ 0 3 ) =p(G_0)* (-\frac{1}{\sigma_0} + \frac{(x - u_0)^2} { \sigma_0^3} ) =p(G0)∗(−σ01+σ03(x−u0)2) = p ( G 0 ) ∗ 1 σ 0 ( ( x − u 0 ) 2 σ 0 2 − 1 ) =p(G_0)* \frac{1}{\sigma_0}( \frac{(x - u_0)^2} { \sigma_0^2} - 1 ) =p(G0)∗σ01(σ02(x−u0)2−1)
则 σ 0 \sigma_0 σ0的更新:
σ ^ 0 = σ 0 + p ( G 0 ) ∗ 1 σ 0 ( ( x − u 0 ) 2 σ 0 2 − 1 ) ∗ c \hat \sigma_0 = \sigma_0 + p(G_0)* \frac{1}{\sigma_0}( \frac{(x - u_0)^2} { \sigma_0^2} - 1 )*c σ^0=σ0+p(G0)∗σ01(σ02(x−u0)2−1)∗c
同理,对第二高斯分布以及语音的两个高斯分布的均值更新的一般函数为:
σ ^ = σ + p ( G ) ∗ 1 σ ( ( x − u ) 2 σ 2 − 1 ) ∗ c \hat \sigma = \sigma + p(G)* \frac{1}{\sigma}( \frac{(x - u)^2} { \sigma^2} - 1 )*c σ^=σ+p(G)∗σ1(σ2(x−u)2−1)∗c
如下面代码,对噪声的方差参数更新:
3.2.3 假设检验(hypothesis-test)

在此小结之前,主要讲解如何通过频带划分提取特征、高斯分布概率的数值求解、模型的自适应更新等技术,如上述代码注释的第一句:Calculates the probabilities for both speech and background noise using Gaussian Mixture Models (GMM)。这只是该算法的技术层面,接下来将讲解算法的核心思想:A hypothesis-test is performed to decide which type of signal is most probable.
假设检验可以用来判断样本与样本或样本与总体的差异是由抽样误差引起的还是由于本质上差别引起的,其基本原理是对总体的特征做出某种假设,然后通过抽样研究的统计推理,进而做出对此假设是接受还是拒绝的推断。
提出假设的形式:
原假设 H 0 H0 H0 : 样本与总体或样本与样本间的差异是由抽样误差引起的;
备择假设 H 1 H1 H1:样本与总体或样本与样本间存在本质差异。
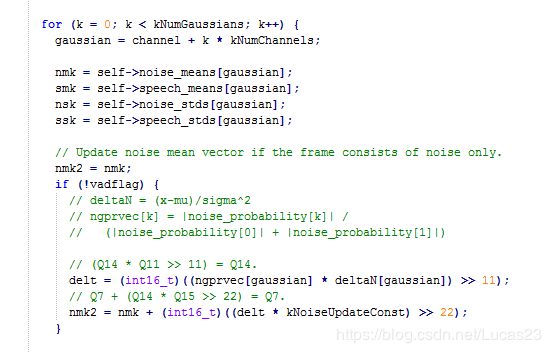
那么算法中原假设 H 0 H0 H0 :噪声,备择假设 H 1 H1 H1:语音 ;而原假设的总体特征,即噪声的特征是频带能量相对小的,其实现就是WebRtcVad_FindMinimum函数:

该函数逻辑比较简单,就是跟踪16个最小值,每个最小值最长更新期限为100帧,并返回5个最小值的中值的平滑值。(为什么不跟踪5个就行了?首先最小值需要在最近一定时期内更新,噪声可能只在短时间平稳;如果只有5个,那么更新很容易将目前一个较大的值记录5个最小值之一,因此需要跟踪更多,允许使一些期限到的最小更新当前值,同时还有候选的真正小最值重新形成5个最小值。)
通过上述函数获得最小值做为调整噪声模型均值:
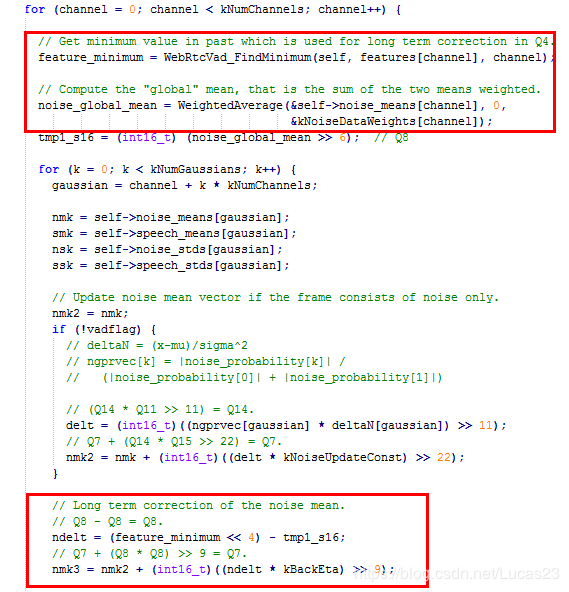
上述约代码束调整噪声的整体分布的均值向feature_minimun比例调整,从而保持原假设 H 0 H0 H0,维持误差。

更新噪声分布的整体均值后,上面的代码又比例调整噪声分布和语音分布的均值的相对距离,即保证备择假设 H 1 H1 H1,使有本质差异。
也就是通过WebRtcVad_FindMinimum的最小值,进行噪声假设,从而构建了噪声和语音两个分布模型。
对于语音信号增强,如降噪,通常都是跟踪信号中能量较小值来假设为噪声,只是具体实现方法不同。这部分是基础,影响两个分布的准确度,可在这里进行算法优化。
假设检验标准:
统计推断假设检验判决标准,一般就是最大后验概率准则:
p ( H 0 ∣ x ) p ( H 1 ∣ x ) > 1 , 则 接 受 为 原 假 设 \frac{p(H0|x)}{p(H1|x)}>1, 则接受为原假设 p(H1∣x)p(H0∣x)>1,则接受为原假设
算法中在3.1节所说,转换为似然概率比进行判断。
4 鲁棒性输出

上面代码为整个算法最后的判决输出,为了保证判决为语音鲁棒性及连贯性,采用非语音滞后判决,使短时间隔的噪声也判决输出为语音标志。