数据预处理--噪声
1.噪声是什么？数据集中的干扰数据（对场景描述不准确的数据）
2.噪声怎么产生的？举个例子：手机信号来自于基站发射的电磁波，有的地方比较强，有的地方比较弱。运营商的工程师会负责统计不同区域信号强弱来进行网络规划，工程师采集信号的方法就是将一个信号接受终端固定到车上，然后开车绕着基站转，信号终端就会自动采集不同区域的信号强度，生成一份数据。但是如果车在采集过程中遇到了突发事件、急刹车，就可能会对信号采集造成一定的影响，生成噪声数据。
3.噪声对模型训练有什么影响？很多算法，特别是线性算法，都是通过迭代来获取最优解的，如果数据中含有大量的噪声数据，将会大大的影响数据的收敛速度，甚至对于训练生成模型的准确也会有很大的副作用。
4.去除噪声的方法：根据不同的业务场景有不同的处理方法，这里只提出正态分布3σ原则。正态分布也叫常态分布，是连续随机变量概率分布的一种，自然界、人类社会、心理、教育中大量现象均按正态分布，如能力的高低、学生成绩的好坏都属于正态分布，我们可以把数据集的质量分布立杰成一个正态分布。它会随着随机变量的平均数、标准差与单位不同而有不同的分布形态。正态分布可以表示成一种概率密度函数。
正态分布公式
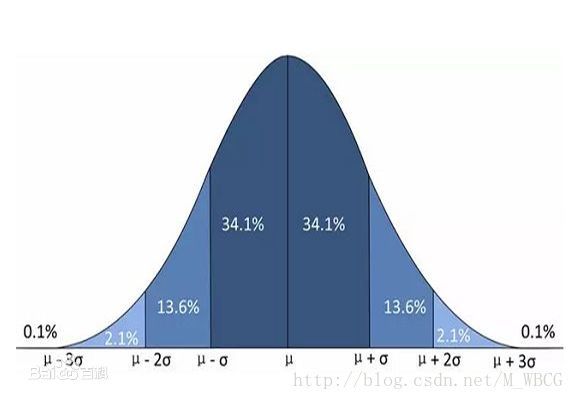
正态分布具有这样的特点：x落在（μ-3σ，μ+3σ）以外的概率小于千分之三。根据这一特点，我们可以通过计算数据集的标准差，把三倍于数据集的标准差的点设想为噪声数据排除。
示例
from __future__ import division
mat = [[19, 26, 63], [13, 62, 65], [16, 69, 15], [14, 56, 17], [19, 6, 15], [11, 42, 15], [18, 58, 36], [12, 77, 33],
[10, 75, 47], [15, 54, 70], [10017, 1421077, 4169]]
# 获得矩阵的字段数量
def width(lst):
i = 0;
for j in lst[0]:
i += 1
return i
# 得到每个字段的平均值
def GetAverage(mat):
n = len(mat)
m = width(mat)
num = [0] * m
for i in range(0, m):
for j in mat:
num[i] += j[i]
num[i] = num[i] / n
return num
# 获得每个字段的标准差
def GetVar(average, mat):
ListMat = []
for i in mat:
ListMat.append(list(map(lambda x: x[0] - x[1], zip(average, i))))
n = len(ListMat)
m = width(ListMat)
num = [0] * m
for j in range(0, m):
for i in ListMat:
num[j] += i[j] * i[j]
num[j] /= n
return num
# 获得每个字段的标准差
def GetStandardDeviation(mat):
return list(map(lambda x:x**0.5,mat))
# 对数据集去噪声
def DenoisMat(mat):
average = GetAverage(mat)
variance = GetVar(average, mat)
standardDeviation=GetStandardDeviation(variance)
section = list(map(lambda x: x[0] + 3*x[1], zip(average, standardDeviation)))
n = len(mat)
m = width(mat)
num = [0] * m
denoisMat = []
noDenoisMat=[]
for i in mat:
for j in range(0, m):
if i[j] > section[j]:
denoisMat.append(i)
break
if j==(m-1):
noDenoisMat.append(i)
print("去除完噪声的数据：")
print(noDenoisMat)
print("噪声数据：")
return denoisMat
if __name__ == '__main__':
print("初始数据：")
print(mat)
print(DenoisMat(mat))
数据过滤：一组数据中，里面有一个字段对于结果没有任何的意义，就可以将该字段过滤掉。就例如一组数据的用户ID不具备描述行为特性的含义。