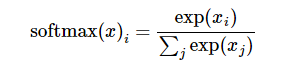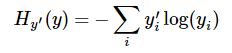TensorFlow入门:损失函数
TensorFlow的Cross_Entropy实现
tf.nn.sigmoid_cross_entropy_with_logits(_sentinel=None,labels=None, logits=None, name=None)
sigmoid_cross_entropy_with_logits是TensorFlow最早实现的交叉熵算法。这个函数的输入是logits和labels,logits就是神经网络模型中的 W * X矩阵,注意不需要经过sigmoid,而labels的shape和logits相同,就是正确的标签值,例如这个模型一次要判断100张图是否包含10种动物,这两个输入的shape都是[100, 10]。注释中还提到这10个分类之间是独立的、不要求是互斥,这种问题我们称为多目标(多标签)分类,例如判断图片中是否包含10种动物中的一种或几种,标签值可以包含多个1或0个1。还有一种问题是多分类问题(类别之间是互斥的),例如我们对年龄特征分为5段,只允许5个值有且只有1个值为1,就不可以直接用这个函数。注:掷一次硬币,A表示正面,B表示背面,二者互斥;掷两次硬币,A表示第一次正面,B表示第二次背面,二者独立。
可以看到这就是标准的Cross Entropy算法实现,对W * X得到的值进行sigmoid激活,保证取值在0到1之间,然后放在交叉熵的函数中计算Loss。对于二分类问题这样做没问题,但对于前面提到的多分类,例如年轻取值范围在0~4,目标值也在0~4,这里如果经过sigmoid后预测值就限制在0到1之间,而且公式中的1 - z就会出现负数,仔细想一下0到4之间还不存在线性关系,如果直接把label值带入计算肯定会有非常大的误差。因此对于多分类问题是不能直接代入的,那其实我们可以灵活变通,把5个年龄段的预测用onehot encoding变成5维的label,训练时当做5个不同的目标来训练即可,但不保证只有一个为1,对于这类问题TensorFlow又提供了基于Softmax的交叉熵函数。
tf.nn.softmax_cross_entropy_with_logits(_sentinel=None,labels=None, logits=None, dim=-1, name=None)
Softmax本身的算法很简单,就是把所有值用e的n次方计算出来,求和后算每个值占的比率,保证总和为1,一般我们可以认为Softmax出来的就是confidence也就是概率。
第一个参数logits:就是神经网络最后一层的输出,如果有batch的话,它的大小就是[batchsize,num_classes],单样本的话,大小就是num_classes
第二个参数labels:实际的标签,大小同上。
softmax_cross_entropy_with_logits和sigmoid_cross_entropy_with_logits很不一样,输入是类似的logits和lables的shape一样,但这里要求分类的结果是互斥的,保证只有一个字段有值,例如CIFAR-10中图片只能分一类而不像前面判断是否包含多类动物。这是因为在函数头的注释中我们看到,这个函数传入的logits是unscaled的,既不做sigmoid也不做softmax,因为函数实现会在内部更高效得使用softmax,对于任意的输入经过softmax都会变成和为1的概率预测值,这个值就可以代入变形的Cross Entroy算法- y * ln(a) - (1 - y) * ln(1 - a)算法中,得到有意义的Loss值了。如果是多目标问题,经过softmax就不会得到多个和为1的概率,而且label有多个1也无法计算交叉熵,因此这个函数只适合单目标的二分类或者多分类问题
注意:(1)如果labels的每一行是one-hot表示,也就是只有一个地方为1,其他地方为0,可以使用tf.sparse_softmax_cross_entropy_with_logits()(2)这个函数的返回值并不是一个数,而是一个向量,如果要求交叉熵,我们要再做一步tf.reduce_sum操作,就是对向量里面所有元素求和,最后才得到交叉熵,如果求loss,则要做一步tf.reduce_mean操作,对向量求均值!
警告:(1)这个操作的输入logits是未经缩放的,该操作内部会对logits使用softmax操作;(2)参数labels,logits必须有相同的形状 [batch_size, num_classes] 和相同的类型(float16, float32,float64)中的一种。
该函数具体的执行过程分两步:首先对logits做一个Softmax,
第二步就是将第一步的输出与样本的实际标签labels做一个交叉熵。
tf.nn.sparse_softmax_cross_entropy_with_logits(_sentinel=None,labels=None, logits=None, name=None)
sparse_softmax_cross_entropy_with_logits是softmax_cross_entropy_with_logits的易用版本,除了输入参数不同,作用和算法实现都是一样的。前面提到softmax_cross_entropy_with_logits的输入必须是类似onehot encoding的多维特征,但CIFAR-10、ImageNet和大部分分类场景都只有一个分类目标,label值都是从0编码的整数,每次转成onehot encoding比较麻烦,有没有更好的方法呢?答案就是用sparse_softmax_cross_entropy_with_logits,它的第一个参数logits和前面一样,shape是[batch_size, num_classes],而第二个参数labels以前也必须是[batch_size, num_classes]否则无法做Cross Entropy,这个函数改为限制更强的[batch_size],而值必须是从0开始编码的int32或int64,而且值范围是[0, num_class),如果我们从1开始编码或者步长大于1,会导致某些label值超过这个范围,代码会直接报错退出。这也很好理解,TensorFlow通过这样的限制才能知道用户传入的3、6或者9对应是哪个class,最后可以在内部高效实现类似的onehot encoding,这只是简化用户的输入而已,如果用户已经做了onehot encoding那可以直接使用不带“sparse”的softmax_cross_entropy_with_logits函数。
tf.nn.weighted_cross_entropy_with_logits(targets, logits, pos_weight, name=None)
weighted_sigmoid_cross_entropy_with_logits是sigmoid_cross_entropy_with_logits的拓展版,输入参数和实现和后者差不多,可以多支持一个pos_weight参数,目的是可以增加或者减小正样本在算Cross Entropy时的Loss。实现原理很简单,在传统基于sigmoid的交叉熵算法上,正样本算出的值乘以某个系数接口,算法实现如下。
总结
这就是TensorFlow目前提供的有关Cross Entropy的函数实现,用户需要理解多目标和多分类的场景,根据业务需求(分类目标是否独立和互斥)来选择基于sigmoid或者softmax的实现,如果使用sigmoid目前还支持加权的实现,如果使用softmax我们可以自己做onehot coding或者使用更易用的sparse_softmax_cross_entropy_with_logits函数。
TensorFlow提供的Cross Entropy函数基本覆盖了多目标和多分类的问题,但如果同时是多目标多分类的场景,肯定是无法使用softmax_cross_entropy_with_logits,如果使用sigmoid_cross_entropy_with_logits我们就把多分类的特征都认为是独立的特征,而实际上他们有且只有一个为1的非独立特征,计算Loss时不如Softmax有效。这里可以预测下,未来TensorFlow社区将会实现更多的op解决类似的问题,我们也期待更多人参与TensorFlow贡献算法和代码 :)