UnityShader——GPU GEM大气散射源码解析

这段时间磨磨蹭蹭的总算是把大气散射这块啃了下，没有去看论文原文了，主要参考的就是 GPU Gem2 里的这篇文章，要想更系统的了解大气散射相关发展的话可以看乐乐姐的这篇专栏

如果对渲染方程没有概念的话最好先阅读我之前的这篇博客

---

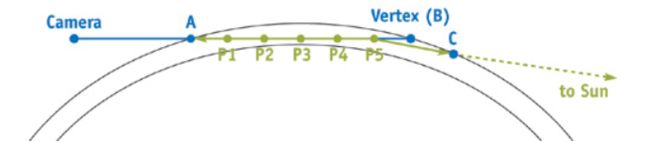
如图所示，大气散射其实就是图中绿色线条部分的光传播过程

首先简单的介绍下大气的两个散射模型：

Rayleigh Scattering：
由大气中的小分子造成，波长短的蓝光散射得更多，最终从各个方向到达观察者的眼睛
阳光在日落时逐渐变成黄色、红色是因为光在大气中的路程变长了，波长短的蓝光绿光在到达眼睛前就散射得差不多了

Mie Scattering：
由大气中较大的粒子造成，等量的散射所有波长的光线，在有雾的天气，让天空看起来是灰色并在太阳周围造成光晕

两个散射模型可以统一到同一个相函数中：

F(θ,g)=3×(1−g2)2×(2+g2)×1+cos2θ(1+g2−2×g×cosθ)32 F ( θ , g ) = 3 × ( 1 − g 2 ) 2 × ( 2 + g 2 ) × 1 + c o s 2 θ ( 1 + g 2 − 2 × g × c o s θ ) 3 2

方程描述了给予常数 g g 和角度 θ θ 有多少光线反射到了相机方向，其中 θ θ 是图中两个绿色线条的夹角， g=0 g = 0 时方程可近似描述 Rayleigh scattering，对于 MieScattering， g g 通常在 −0.75 − 0.75 到 −0.999 − 0.999 之间

接下来是 out-scattering

t(PaPb,λ)=4π×K(λ)×∫PbPaexp(−hH0)ds t ( P a P b , λ ) = 4 π × K ( λ ) × ∫ P a P b e x p ( − h H 0 ) d s

其中积分部分为光学厚度， h h 为归一化后的采样点高度， H0 H 0 为大气密度等于平均值时的高度，取 0.25， K K 为散射常数

In-Scattering

Iv(λ)=Is(λ)×K(λ)×F(θ,g)×∫PbPa(exp(−hH0×exp(−t(PPc,λ)−t(PPa,λ)))ds I v ( λ ) = I s ( λ ) × K ( λ ) × F ( θ , g ) × ∫ P a P b ( e x p ( − h H 0 × e x p ( − t ( P P c , λ ) − t ( P P a , λ ) ) ) d s

该方程描述了在传播过程中有多少光通过散射的形式加入了该光路中，其中，在 Pa P a 到 Pb P b 的每个采样点 P P 上， PPa P P a 是点到相机的射线， PPc P P c 是点到太阳的射线， Is I s 为太阳光，对于每一个采样点，积分部分描述了太阳光一路散射到改点，然后又一路散射到相机这么长的路程会造成的损失，剩余的再通过相函数筛选才能真正到达相机

---

然而这么多积分，实际计算起来性能肯定捉急，这里便是文章的核心，GPU GEM的代码中使用了LUT的思想，使得最终计算只需要计算一个积分

首先，设X轴为高度，Y轴为光学厚度，图如所示，我们可以将所有角度的光学厚度绘制出来，然后将所有角度的曲线归一化，即 x=0 x = 0 时 y=1 y = 1 ， 朝 x=1 x = 1 ， y=0 y = 0 方向，此时所有的曲线都几乎落在了 y=exp(−4x) y = e x p ( − 4 x ) 的曲线上，恰好是 H0=0.25 H 0 = 0.25 时的结果

在前面的构造中，我们对不同角度的曲线进行了缩放操作，因此我们需要知道，在特定高度下，每个角度缩放的值，这里原文作者自己弄了个函数来做逼近，即：

float scale(float fCos)
{
    float x = 1.0 - fCos;
    return 0.25 * exp(-0.00287 + x*(0.459 + x*(3.83 + x*(-6.80 + x*5.25))));
}

但只有大气厚度为星球半径的 0.25% 时该逼近公式才是准确的
这样，对于一个采样点，我们只需要知道其一个角度的积分，通过 scale 函数便可得到其在其他角度的积分，而这个积分我们甚至也不用算，因为其结果归一化后几乎都落在了 y=exp(−4x) y = e x p ( − 4 x ) 这条曲线上，但这里的问题是，积分中的 x（高度）不是线性变化的，在角度超过90度以后误差较大，如上图所示，当大气层厚度像比如星球半径很小的时候，超过90度后太多射线就会与星球相交了，因此超过90度太多的情况不用考虑，剩余角度的误差都在可接受范围内

---

接下来，我们详细的解析散射计算中的代码：

float3 v3Pos = mul(unity_ObjectToWorld, v.vertex).xyz - v3Translate;
float3 v3Ray = v3Pos - v3CameraPos;
float fFar = length(v3Ray);
v3Ray /= fFar;

Shader 的 Cull 模式为 Cull Front，只考虑了相机在大气层外的情况
首先得到相机到 Back 顶点的单位向量

float fNear = getNearIntersection(v3CameraPos, v3Ray, fCameraHeight2, fOuterRadius2);

然后得到该射线与 Front 的交点，这里方法很多，可以参考体积光这篇文章的方法

float3 v3Start = v3CameraPos + v3Ray * fNear;

fFar -= fNear;

float fStartAngle = dot(v3Ray, v3Start) / fOuterRadius;

float fStartDepth = exp(-fInvScaleDepth);

float fStartOffset = fStartDepth * scale(fStartAngle);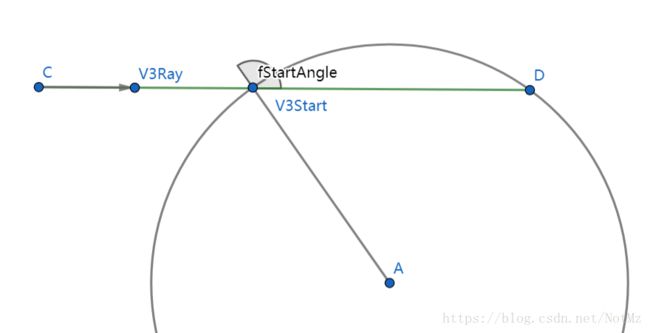

其中 fInvScaleDepth 即 1/H0 1 / H 0 ，所以

fStartDepth=exp(−1/H0) f S t a r t D e p t h = e x p ( − 1 / H 0 )

即高度为1，角度为0时的归一化光学厚度，通过 scale 函数得到当前角度下的实际光学厚度

float fSampleLength = fFar / fSamples;

float fScaledLength = fSampleLength * fScale;

float3 v3SampleRay = v3Ray * fSampleLength;

float3 v3SamplePoint = v3Start + v3SampleRay * 0.5;

这里开始计算第一个采样点的位置，其中 fScale 为 1/H 1 / H , H H 为大气总高度（现实中大气应该是没有边界的，但为了计算方便我们还是设置了一个高度），fScale 将采样步长缩放到到大气总高度为1的比例尺中

float3 v3FrontColor = float3(0.0, 0.0, 0.0);

 for(int i=0; ifloat fHeight = length(v3SamplePoint);

   float fDepth = exp(fScaleOverScaleDepth * (fInnerRadius - fHeight));

   float fLightAngle = dot(v3LightDir, v3SamplePoint) / fHeight;

   float fCameraAngle = dot(v3Ray, v3SamplePoint) / fHeight;

   float fScatter = (fStartOffset + fDepth * (scale(fLightAngle) - scale(fCameraAngle)));

   float3 v3Attenuate = exp(-fScatter * (v3InvWavelength * fKr4PI + fKm4PI));

   v3FrontColor += v3Attenuate * (fDepth * fScaledLength);

   v3SamplePoint += v3SampleRay;

  }

其中 fScaleOverScaleDepth 为 H0/H H 0 / H ，fInnerRadius 为星球半径， 可得

fScaleOverScaleDepth=exp(H0/H∗h) f S c a l e O v e r S c a l e D e p t h = e x p ( H 0 / H ∗ h )

就是采样点高度角度为0时的光学厚度

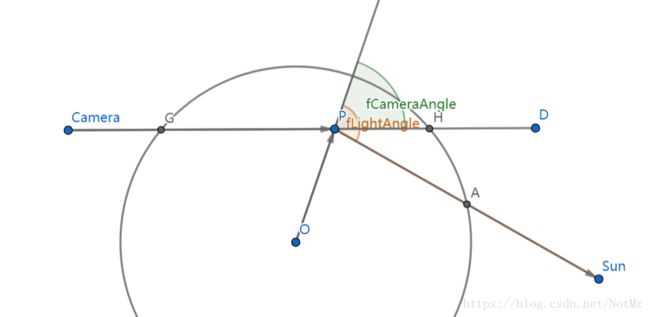
如图所示，fDepth*(scale(fLightAngle) - scale(fCameraAngle))表示 PA - PH，而 fStartOffset 表示 GH 之间的光学厚度，因此 fScatter 即 GP +PA 的光学厚度，也就是第一张图中绿色实线部分，v3Attenuate 则就是 out-scattering了，剩下的就是通过循环计算In-Scattering的积分了，为了效果，相函数部分放在了 frag shader 中计算

最终效果如下：

至于相机在大气中的情况，依然可以通过该方法计算，起始点就是相机位置，但把两个 Sphere 放大来实现感觉有点太蠢了，找找好的实现再来补吧
to be continue…