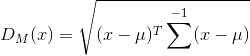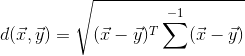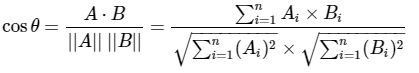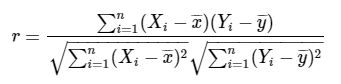几种距离度量方法的简介、区别和应用场景
目录
前言
几种常见距离度量方法
欧几里得距离
简介
公式
曼哈顿距离(Manhattan Distance)
简介
公式
应用场景
切比雪夫距离
简介
公式
闵科夫斯基距离
简介
公式
缺点
马氏距离
简介
公式
汉明距离
简介
应用:
余弦相似度
简介
公式
杰卡德距离
皮尔森相关系数
简介
公式
编辑距离
K-L散度
几种常见的距离度量比较与应用
曼哈顿距离、欧氏距离、皮尔逊相关系数
距离度量,越小越相似
相似度度量,越大越相似
欧氏距离与余弦相似度
前言
在机器学习与数据挖掘中,我们需要知道个体间差异的大小,进而评价个体的相似性和类别。最常见的是数据分析中的相关分析,数据挖掘中的分类和聚类算法,如K最近邻(KNN)和K均值(K-Means)等等。根据数据特性的不同可以采用不同的度量方法。
几种常见距离度量方法
欧几里得距离
简介
欧式距离是最容易直观理解的距离度量方法,两点间在空间中的距离一般都是指欧氏距离。
公式
二维平面上点a(x1,y1)与b(x2,y2)间的欧氏距离。
![]()
三维空间点a(x1,y1,z1)与b(x2,y2,z2)间的欧式距离:
![]()
n维空间点a(x11,x12,...,x1n)与b(x21,x22,...,x2n)间的欧氏距离(两个n维向量):
曼哈顿距离(Manhattan Distance)
简介
在曼哈顿街区,从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是曼哈顿距离。
用一句话来说就是:两个点在标准坐标系上的绝对轴距总和。
公式
二维平面两点a(x1,y1)和b(x2,y2)间的曼哈顿距离:
![]()
n维空间点a(x11,x12,...,x1n)与b(x21,x22,...,x2n)的曼哈顿距离:
应用场景
-
剑指Offer------网易笔试之解救小易(牛客网在线提交)
有一片1000*1000的草地,小易初始站在(1,1)(最左上角的位置)。小易在每一秒会横向或者纵向移动到相邻的草地上吃草(小易不会走出边界)。
大反派超超想去捕捉可爱的小易,他手里有n个陷阱。第i个陷阱被安置在横坐标为xi ,纵坐标为yi 的位置上,小易一旦走入一个陷阱,将会被超超捕捉。
你为了去解救小易,需要知道小易最少多少秒可能会走入一个陷阱,从而提前解救小易。
输入描述:
第一行为一个整数n(n ≤ 1000),表示超超一共拥有n个陷阱。
第二行有n个整数xi,表示第i个陷阱的横坐标
第三行有n个整数yi,表示第i个陷阱的纵坐标
保证坐标都在草地范围内。
输出描述:
输出一个整数,表示小易最少可能多少秒就落入超超的陷阱
输入例子:
3
4 6 8
1 2 1
输出例子:
3
- 思路:利用曼哈顿距离计算最短距离。
- 实现:
-
#includeint main(){ int n; scanf("%d",&n); int loop[n][n]; int j; for(j=0;j
切比雪夫距离
简介
国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个放个中的任意一个。国王从各自(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫做切比雪夫距离。
数学上,切比雪夫距离或是![]() 度量是向量空间中的一种度量,两个点之间的距离定义为其各坐标数值差的最大值。
度量是向量空间中的一种度量,两个点之间的距离定义为其各坐标数值差的最大值。
公式
二维平面两点a(x1,y1)和b(x2,y2)间的切比雪夫距离
![]()
n维空间点a(x11,x12,...,x1n)与b(x21,x22,...,x2n)的切比雪夫距离
闵科夫斯基距离
简介
闵科夫斯基距离不是一种距离,而是一组距离的定义,是对多个距离度量公式的概括性的表述。
公式
两个n为变量a(x11,x12,...,x1n)与b(x21,x22,...,x2n)间的闵科夫斯基距离定义为
其中p是一个变参数:
当p=1时,就是曼哈顿距离;
当p=2时,就是欧氏距离;
当p->∞时,就是切比雪夫距离。
因此,根据变参数的不同,闵科夫斯基距离可以表示某一类/种的距离。
p值越大,单个维度的差值大小会对整体距离有更大的影响。
缺点
- 将各个分量的量纲(scale),也就是“单位”相同的看待了;
- 未考虑各个分量的分布(期望、方差等)可能是不同的。
eg:二维样本(身高[单位:cm],体重[单位:kg]),现有三个样本:a(180,50),b(190,50),c(180,60)。那么a与b的闵氏距离(无论是曼哈顿距离、欧氏距离或切比雪夫距离)等于a与c的闵氏距离。但实际上身高的10cm并不能和体重的10kg划等号。
马氏距离
简介
表示数据的协方差距离,它是一种有效的计算两个未知样本集的相似度的方法。
与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的,即独立于测量尺度。
如果协方差矩阵为单位矩阵,马氏距离就简化为欧氏距离。
如果协方差矩阵为对角矩阵,其也可称为正规化的马氏距离。
公式
对于一个均值![]() ,协方差矩阵为Σ ,其马氏距离为:
,协方差矩阵为Σ ,其马氏距离为:
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为Σ的随机变量 ![]() 与
与![]() 的差异程度
的差异程度
汉明距离
简介
在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。
eg:
- 1011101与1001001之间的汉明距离是2
- 2143896与2233796之间的汉明距离是3
- toned 与 roses 之间的汉明距离是3
应用:
UVA-1368 DNA Consensus String DNA序列
余弦相似度
简介
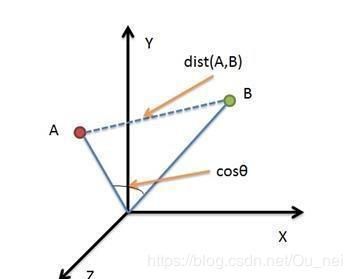
余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。
0度角的余弦值是1,而其他任何角度的余弦值都不大于1;并且其最小值是-1。
两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。
两个相同方向的向量,余弦相似度的值为1;两个向量夹角为90°时,余弦相速度的值为0;两个向量指向完全相反的方向时,余弦相似度的值为-1。这个结果与向量的长度无关,仅仅与向量的指向方向相关。
公式
给定两个属性向量, A和B,其余弦相似性θ由点积和向量长度给出
这里的![]() 和
和![]() 分别代表向量A和B的各分向量。
分别代表向量A和B的各分向量。
杰卡德距离
https://www.iteblog.com/archives/2317.html
皮尔森相关系数
简介
也称皮尔森积矩相关系数,是一种线性相关系数。皮尔森相关系数是用来反映两个变量下你选哪个相关程度的统计量。相关系数用r表示,其中n为样本量,分别为两个变量的观测值和均值。r描述的是两个变量间线性相关强弱的程度。r的绝对值越大表示相关性越强。
公式
分子是两个集合的交集大小,分母是两个集合大小的几何平均值。是余弦相似性的一种形式。
编辑距离
K-L散度
几种常见的距离度量比较与应用
曼哈顿距离、欧氏距离、皮尔逊相关系数
- 如果数据存在“分数膨胀“问题,就使用皮尔逊相关系数
- 如果数据比较密集,变量之间基本都存在共有值,且这些距离数据都是非常重要的,那就使用欧几里得或者曼哈顿距离
- 如果数据是稀疏的,就使用余弦相似度
- 在线音乐网站的用户评分例子https://blog.csdn.net/Gamer_gyt/article/details/78037780
- 由皮尔逊相关系数可以得出评分分值差别很大的两个用户其实喜好是完全一致的。 找相似用户。
- 如果数据的维度不一样,用欧氏距离或曼哈顿距离是不公平的。 在数据完整的情况下效果好。
距离度量,越小越相似
曼哈顿距离、欧氏距离、切比雪夫距离等。
相似度度量,越大越相似
应用于协同过滤。
欧氏距离与余弦相似度
- 欧式距离能体现个体数值特征的绝对差异,多用于需要从维度的数值大小中体现差异的分析,如使用用户行为指标分析用户价值的相似度或差异。
- 余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感,多用于使用用户对内容评分来区别用户兴趣的相似度和差异,同时修正了用户间可能存在的度量标准不统一的问题。(因为余弦相似度对绝对值不敏感)
- eg:如某T恤从100块降到了50块(A(100,50)),某西装从1000块降到了500块(B(1000,500)),那么T恤和西装都是降价了50%,两者的价格变动趋势一致,可以用余弦相似度衡量,即两者有很高的变化趋势相似度,但是从商品价格本身的角度来说,两者相差了好几百块的差距,欧氏距离较大,即两者有较低的价格相似度。
- 如果要对电子商务用户做聚类,区分高价值用户和低价值用户,用消费次数和平均消费额,这个时候用余弦相似度是不恰当的,因为它会将(2,10)和(10,50)的用户算成相似用户,但显然后者的价值高得多,因为这个时候需要注重数值上的差异,而不是维度之间的差异,故要用欧氏距离。
- 两用户只对两件商品评分,向量分别为(3,3)和(5,5),显然这两个用户对两件商品的偏好是一样的,但是欧式距离给出的相似度显然没有余弦相似度合理。
- https://blog.csdn.net/luckoovy/article/details/81668639



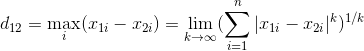
![d_{12}=\sqrt[p]{\sum_{k=1}^{n}|x_{1k}-x_{2k}|^p}](http://img.e-com-net.com/image/info8/3fc8b3c8e9614e9a87516bc00bf18aef.gif)