华北水利水电大学ACM第二届校赛题解
A: Xor and Sum
题目描述
给定一个大小为N的数组A,第i个元素为Ai。
问有多少的子区间[LR],满足区间数值异或和等于区间数值和,即:
- Al xor Al+1 xor…xor Ar = Al + Al+1 +…+Ar(l+1表示下标)
- a和b的xor即为a和b二进制表示按位取xor得到新数c的十进制表示
5和12的xor计算如下:
510=01012
(12)10=(1100)2
01012xor11002=(1001)2
(1001)2=(9)10
输入
第一行给定一个整数N。
第二行给定N个整数,第i个数即为Ai。
1≤N≤2×10^5
0≤A_i≤2^30
输出
输出满足条件的子区间LR的数量。
样例输入
10
0 0 740 361 473 0 0 826 479 974
样例输出
18思路:比赛的时候晃眼看了一下以为是数位dp什么的,就是没什么头绪。没做
赛后补题,挺妙的。
题解:
xor运算可以视为二进制下没有进位的加法,加法运算本身是有进位的加法。
那么可以简单得出这样一个性质:对于一个区间而言,如果异或和加法答案一样,那么把区间缩小答案肯定还是一样;如果异或和加法答案不一样,那么把区间扩大答案肯定还是不一样。
于是我们就可以枚举区间右端点,去寻找最小的左端点,这个区间异或等于区间和,那么以这个区间右端点的合法区间个数就是区间的长度(左端点往里缩都是合法的)。
这个可以预处理出前缀和还有前缀异或和,用双指针维护出来。
xor运算可以视为二进制下没有进位的加法,加法运算本身是有进位的加法。
那么可以简单得出这样一个性质:对于一个区间而言,如果异或和加法答案一样,那么把区间缩小答案肯定还是一样;如果异或和加法答案不一样,那么把区间扩大答案肯定还是不一样。
于是我们就可以枚举区间右端点,去寻找最小的左端点,这个区间异或等于区间和,那么以这个区间右端点的合法区间个数就是区间的长度(左端点往里缩都是合法的)。
这个可以预处理出前缀和还有前缀异或和,用双指针维护出来。
代码如下:
#include
#include
#include
#include
#include
#include
#include
#include
#define per(i,a,b) for(int i=a;i<=b;++i)
#define rep(i,a,b) for(int i=a;i>=b;--i)
#define inf 0xf3f3f3f
#define ll long long int
using namespace std;
int p[200005];
int s[200005];
int z[200005];
int main()
{
int m,a;
cin>>m;
z[0]=0;s[0]=0;
per(i,1,m)
{
cin>>a;
s[i]=s[i-1]+a;
z[i]=z[i-1]^a;
}
ll l=0,sum=0;
per(i,1,m)
{
while((z[i]^z[l])!=(s[i]-s[l])) l++;
sum+=i-l;
}
cout< B: 敲7
题目描述
输出7和7的倍数,还有包含7的数字的个数例如(17,27,37...70,71,72,73...)
输入
一个整数N。(N不大于30000)
输出
统计出不大于N的与7有关的数字的个数。如20以内与7有关的数为7、14、17共3个。
样例输入
20样例输出
3思路:水题,判一下就行。
C: 魔法扑克
题目描述
Yellowstar玩扑克总能立于不败之地,原因竟是他会使用魔法,每次使用魔法,能把手里的扑克变换成另一张扑克,但是使用魔法是非常消耗精力的,因此他不在万不得已的情况下不会轻易使用魔法。
某天Yellowstar打德州扑克输光了所有筹码,最后一轮,不得已他只好使用魔法。这轮他手里拿了5张牌,他需要使用魔法把这副牌变成同花顺,称五张牌构成了同花顺,当且仅当它们的数值连续,花色一致。
Yellowstar每次使用魔法能变换一张牌,他想知道最少他需要使用多少次魔法才能把牌变成同花顺。
扑克中一共有52种牌,牌的花色用一个大写字母'A' 'B' 'C' 'D'来表示,而数值用数字('1' '2' … '13')来表示。注意数字1代表ace,在德州扑克中是最大的牌。"1 2 3 4 5" 和 "10 11 12 13 1" 都被认为是连续的。而"11 12 13 1 2"并不是。
输入
第一行是样例数 1 <= T <= 1000
对于每组数据,在一行中有五个字符串代表五张牌。数据保证所有的牌都是不同的。
输出
输出T行,每行一个数表示最少需要使用几次魔法。
样例输入
5
A2 A3 A1 A4 A5
A1 A2 A3 A4 C5
A9 A10 C11 C12 C13
A11 A12 A13 A1 A2
B10 B11 B12 B13 B1
样例输出
0
1
2
1
0
提示
第一个样例存在A1A2A3A4A5这个同花顺,不需要使用魔法。
思路:标解为暴力枚举,我用的是贪心,因为要找最少的非连续牌,所以我们可以找最大连续牌,相减得答案。但因为1的存在,需要进行特判,若有1则需再转化为14再跑一遍取极值。(注意有多个1的情况)
代码如下:
#include
#include
#include
#include
#include
#include
#include
#include D: 最长单词
题目描述
编写一个函数,输入一行字符,将此字符串中最长的单词输出。
输入仅一行,多个单词,每个单词间用一个空格隔开。单词仅由小写字母组成。所有单词的长度和不超过100000。如有多个最长单词,输出最先出现的。
输入
输出
样例输入
I am a student 样例输出
student 思路:签到题
E: 天凤麻雀
题目描述
Yellowstar喜欢麻将,但是他觉得普通麻将不够有趣,于是他自己发明了一种名为天凤麻雀的麻将游戏。
一共有m种牌,编号为1到m,每个人手上一开始有3 * n + 1张牌,每轮摸一张牌,并打出一张牌。一副牌可以胡,需要摸牌之后的3 * n + 2张牌满足以下条件:
1、 拿出两张相同的牌作为雀头
2、 其余的3 * n张牌,分成n组,每组3张牌,每组牌满足是一个顺子或者是刻子。
定义顺子为三张牌的编号为连续的三个数x ,x + 1, x + 2的一组牌 定义刻子为三张牌编号全部相同的一组牌。
某一轮游戏中,Yellowstar起手得到一副牌,他想快速计算出,有几种牌可以让他进行胡牌。
输入
第一行是样例数 1 <= T <= 20。
每组样例第一行给定n,m,表示一共有3 * n + 1张牌,一共有m种牌 (1 <= n m <= 300)。
接下来一行包含3 * n + 1个数字,表示Yellowstar的起手牌,所有数字在1到m范围内。
输出
输出T行,每行一个数表示有几种牌可以让他进行胡牌。
样例输入
1
4 9
1 1 2 2 3 3 5 5 5 7 8 8 8样例输出
3提示
拿到6、7、9三种牌就能胡牌。
思路:比赛时没能做出来,需要考虑的边界极多。
标称思路:
此题和魔法扑克有类似之处,都是用枚举来完成的,考虑把 1-m之间的数字依次加入里面看看是否可以胡牌,如果可以累加一次,输出最好的累加结果即可
注意点:一. 任意一种牌的数量可能会大于4,和现实打牌不一样
二. 枚举时要优化,分一下几个步骤{
1.首先假装加入一张牌,
2. 循环对数量大于2的牌作为雀头3枚举时可以考虑从小到大或从大到小,先把数量大于3等于3的作为刻字,然后再考虑顺子,知道你们有疑问会怀疑就算数量大于等于3也有可能全部用于顺子,但那只可能是中间的牌,形如 111 222 333,或112223334 请认真分析,
4.任意时刻加入的牌要记得再计算完要及时去掉。.}
标程代码:
#include
#include
#include
using namespace std;
int n,m;
int d[405],f[405],ans[405];
bool check()
{
bool bk;
for(int i=1;i<=n;i++)
{
if(d[i]>=2)
{
bk=true;
d[i]-=2;
for(int j=1;j<=n+2;j++) f[j]=d[j];
for(int j=1;j<=n+2;j++)
{
if(f[j]<0){bk=false;break;}
f[j]%=3;f[j+1]-=f[j];f[j+2]-=f[j];
}
d[i]+=2;
if(bk) return true;
}
}
return false;
}
int main()
{
//freopen("test.in", "r", stdin);
//freopen("test.out", "w", stdout);
int T;
scanf("%d", &T);
while (T--) {
memset(d, 0, sizeof(d));
memset(f, 0, sizeof(f));
memset(ans, 0, sizeof(ans));
scanf("%d%d",&m,&n);
int x;
for(int i=1;i<=m*3+1;i++)
{
scanf("%d",&x);
d[x]++;
}
bool bk=false;
for(int i=1;i<=n;i++)
{
d[i]++;
if(check())
{
bk=true;
ans[++ans[0]]=i;
}
d[i]--;
}
printf("%d\n", ans[0]);
}
return 0;
}
F: 第x个数
题目描述
silchen得到了长度为N的一个全排列(n个数字互不相同,并且都在[1n]),现在dark di出了一个问题,他会对于这个数列进行M次操作,并且在M次操作之后他会询问silchen第x个数字是什么。
操作有2种类型:
1.将下标[lr]中的数字变为一个递增数列。
2.将下标[lr]中的数字变为一个递减数列。
现在silchen向你来求助了。
输入
第一行输入一个整数T,代表数据组数,T小于等于5
每组数据第一行输入2个整数,分别表示nm其中n是数列长度,m是操作数,nm均不大于1000.
第二行输入n个整数,表示一个排列.
接下去m行3个整数,olr,o为0表示第一种操作,o为1表示第二种操作,保证l,r范围为1到n,且l <= r。
最后输入一个整数x表示要求第x个数字 x范围为1到n。
输出
输出一个数字,表示第x个数字的大小。
样例输入
1
6 3
1 6 2 5 3 4
0 1 4
1 3 6
0 2 4
3
样例输出
5提示
第一次操作后数列变成 1 2 5 6 3 4
第二次操作后数列变成 1 2 6 5 4 3
第三次操作后数列变成 1 2 5 6 4 3
所以第3个数字是5
思路:题解是用简单dp做,然而这题数据放水了用sort膜也能过。。。。
dp代码:
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
int n,m;
int a[123456];
bool v[123456];
int main(){
// freopen("test.in","r",stdin);
// freopen("9.out","w",stdout);
int N;int x; int o,l,r;
scanf("%d",&N);
while(N--){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
int o,l,r;
for(int i=1;i<=m;i++)
{
cin>>o>>l>>r;
memset(v,0,sizeof(v));
for (int j=l;j<=r;j++) v[a[j]]=1;
if (o==0)
{
int t=l;
for (int j=1;j<=n;j++)
{
if (v[j]==1) a[t++]=j;
}
}
else
{
int t=l;
for (int j=n;j>=1;j--)
{
if (v[j]==1) a[t++]=j;
}
}
}
int x;cin>>x;cout< 模拟代码:
#include
#include
#include
#include
#include
#include
#include
#include G: Han’s Number
题目描述
韩跳跳毕业了,打算换电话号码。由于对原号码的恋恋不舍,韩跳跳对新号码的要求是长度必须和原号码一样。
第一位数字可以从0~9中任选,但是接下来的每位数字必须按new[i]=(new[i-1]+old[i])/2的方式选取,其中new[i]表示新号码的第i位数字,old[i]表示旧号码的第i位数字,并且若(new[i-1]+old[i])能整除2则new[i]唯一,否则new[i]可以是它向上或者向下取整的数。
韩跳跳想知道共有多少个新号码可以选择?
输入
第一行一个数n表示原号码的位数。
第二行n个数old[i]表示原来号码的第i位。
1≤n≤50
0≤old[i]≤9
输出
输出一个整数,表示可以选择的新号码个数
样例输入
3
1 2 3
样例输出
21思路:看完题就知道是dp,然而还是不死心的用dfs去卡了2发,未遂,但自家oj居然给了点百分比反馈。然后依据反馈找出坑点才过。注意dp后要判断是否存在与初始号码重号的情况。
代码如下:
#include
#include
#include
#include
#include
#include
#include
#include H: 集合运算
题目描述
给出两个整数集合A、B,求出他们的交集、并集以及B在A中的余集。
输入
第一行为一个整数n,表示集合A中的元素个数。
第二行有n个互不相同的用空格隔开的整数,表示集合A中的元素。
第三行为一个整数m,表示集合B中的元素个数。
第四行有m个互不相同的用空格隔开的整数,表示集合B中的元素。
集合中的所有元素均为int范围内的整数,n、m< =1000。
输出
第一行按从小到大的顺序输出A、B交集中的所有元素。
第二行按从小到大的顺序输出A、B并集中的所有元素。
第三行按从小到大的顺序输出B在A中的余集中的所有元素
样例输入
5
1 2 3 4 5
5
2 4 6 8 10 样例输出
2 4
1 2 3 4 5 6 8 10
1 3 5 思路:签到题
I: 生命之树
题目描述
Yellowstar拥有一棵N个结点的树标号为1到N,树上有M个结点,每个结点上面有一只受了伤奄奄一息的青蛙,为了拯救这些青蛙,他需要施展生命魔法。但是由于魔力有限,他只能对树上距离它长度不大于D的结点进行施法,并且施法过程中他必须一直停留在一个结点上,一旦移动就无法再次施法。现在他想知道树上一共有多少个结点,满足能让他拯救所有的m只青蛙,你能帮帮他吗?
输入
输入的第一行是样例数 1 <= T <= 20
接下来一行包含三个整数N M D(1<= M <= N <=100000 0 <= D <= N - 1)。
接下来一行包含M个不同数字,A1 ... AN,(1<= Ai <= n),表示标号为Ai的结点上面有一只奄奄一息的青蛙。
接下来N-1行,每行包含两个数字U V (1 <= U V <= N)表示树边,保证读入是一棵树。
输出
输出T行,每行输出一行一个数,表示答案。
样例输入
1
6 2 3
1 2
1 5
2 3
3 4
4 5
5 6
样例输出
3思路:因为状态太差,在傻逼题上浪费了快2个小时,所以这道题没A出来。赛后补的题。题意要求求出满足点的个数。
观察 这些点的特征:这些点都能在d的距离下包含青蛙,而想要在d步下全部包含需要保证相对最远的2只青蛙的距离小于等于2d,也就是说这些点都属于相对最远2点青蛙为圆心,d为半径所画的2个圆的交点。(题目保证了所有青蛙都能被救,也就是说2个圆一定有交点)
所以我们只需要分别对这2个相对最远点进行搜索,标记其他点的距离求其交点即可。即问题简化为类树的直径问题(就是一个子树直径)
代码如下:
#include
#include
#include
#include
#include
#include
#include
#include
#define per(i,a,b) for(int i=a;i<=b;++i)
#define rep(i,a,b) for(int i=a;i>=b;--i)
#define inf 0xf3f3f3f
#define ll long long int
using namespace std;
int n,m,k;
int h[100005];
vectorp[100005];
int vis[100005],d[100005];
int bfs(int x,int y)
{
queueq;
q.push(x);
vis[x]++;
d[x]=0;
while(!q.empty())
{
int z=q.front();
q.pop();
per(i,0,p[z].size()-1)
{
int v=p[z][i];
if(vis[v]==y)
{
vis[v]++;
q.push(v);
d[v]=d[z]+1;
}
}
}
int maxn=-1,s;
per(i,1,n)
{
if(h[i]!=0&&maxn>T;
while(T--)
{
int x,a,b;
cin>>n>>m>>k;
per(i,1,n) h[i]=0,p[i].clear(),vis[i]=0;
while(m--)
{
cin>>x;
h[x]=1;
}
per(i,1,n-1)
{
cin>>a>>b;
p[a].push_back(b);
p[b].push_back(a);
}
int s=bfs(1,0);//找一个端点青蛙
int t=bfs(s,1);//找另一个端点青蛙并标记节点距离(找直径)
memset(h,0,sizeof(h));
per(i,1,n) if(d[i]<=k) h[i]++;//根据节点距离标记第一个圆内点
bfs(t,2);//标记第二个圆内点
int num=0;
per(i,1,n) if(d[i]<=k&&h[i]!=0) num++;//统计交点
printf("%d\n",num);
}
return 0;
} J: Distribution
题目描述
One day Wang and Dong in the Dubai desert expedition discovered an ancient castle. Fortunately they found a map of the castle.The map marks the location of treasures.
They agreed to distribute the treasures according to the following rules:
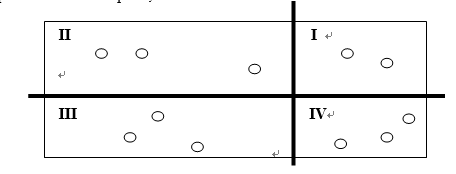
Wang draws a horizontal line on the map and then Dong draws a vertical one so that the map is divided into 4 parts as show below.
Wang will save the treasures in I and III while those situated in II and IV will be taken away by Dong. Wang first draw a horizontal line Dong after the draw a vertical line.
They drew several pairs of lines. For each pair Wang wants to know the difference between their treasures.
It's guaranteed that all the reasures will lie on neither of the lines drew by them.
输入
the first line contains two integers N and M where N is the number of treasures on the map and M indicates how many times they are going to draw the lines. The 2nd to (N+1)-th lines Xi Yi contain the co-ordinates of the treasures and the last M lines consist of the M pairs integers (X Y) which means that the two splitting lines intersect at point (X Y).
( 0 < N M ≤ 1000 ≤ Xi Yi XY ≤ 1000 )
输出
Output contains M lines a single line with a integer the difference described above.
样例输入
10 3
29 22
17 14
18 23
3 15
6 28
30 27
4 1
26 7
8 0
11 21
2 25
5 10
19 24
样例输出
-6
4
4思路:读懂就OK,猜样例也能猜出来。没有一点绕圈子。就是给一个点表示坐标原点,求1,3象限点数与2,4象限点数差
代码如下:
#include
#include
#include
#include
#include
#include
#include
#include
总结:2个队友都脱坑了,搞的我内心十分动摇,近期都没做题,手生异常,直接导致3道签到题wa了8发.......最后靠着题数勉强扳回一点颜面...也够丢脸的,差点被学弟吊打。新组的队友还在磨合中,希望我能在省赛中拿到满意的成绩。ACM这东西...天赋真TMD重要。