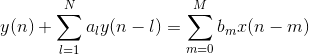【 MATLAB 】使用 MATLAB 求由差分方程表示的滤波器的响应的两种方法
例题:
一个3阶低通滤波器由下面差分方程描述:
y(n) = 0.0181 x(n) + 0.0543 x(n-1) + 0.0543 x(n-2) + 0.0181 x(n-3) + 1.76 y(n-1) - 1.1829 y(n-2) + 0.2781 y(n-3)
画出这个滤波器的幅度和相位响应,并验证它是一个低通滤波器。
第一种方法是博文里给出的:
【 MATLAB 】用 MATLAB 实现离散时间傅里叶变换(DTFT)的两个案例分析
第二个案例中,类比,如果我知道一个LTI系统的脉冲响应h(n),那么我也能求出它的频率响应:
k = [0:M];
n = [n1:n2];
X = x * (exp(-j * pi/M)).^(n'*k);
博文里面由具体的推荐,上述程序中X就是频率响应,也就是x的DTFT,如果x换成h,则X可以换成H。
第二种方法是,通过差分方程直接求出系统的频率响应,求解的方法是通过向量化的方法。
设某一LTI系统的差分方程表示为:
可以用一种简单的矩阵向量乘法来完成。如果在![]() 的
的![]() 个等分频率上求
个等分频率上求![]() ,那么
,那么
注意,上述的b以及a向量都是行向量。
先给出第一种方法的脚本:
clc
clear
close all
b = [0.0181,0.0543,0.0543,0.0181];
a = [1.0000,-1.7600,1.1829,-0.2781];
[h,t]=impz(b,a);
k = [0:500];
w = (pi/500)*k;
t = t';
h = h';
H = h * ( exp(-j*pi/500) ).^(t'*k);
magH = abs(H);
angH = angle(H);
subplot(2,1,1);
plot(w/pi,magH);
title('Magnitude part');
subplot(2,1,2);
plot(w/pi,angH);
title('Angle part');这种方法的思路是通过差分方程可以得到有理传递函数或者频率响应的分子和分母系数,通过impz函数得到脉冲响应,之后由脉冲响应h(n)得到频率响应。
clc
clear
close all
b = [0.0181,0.0543,0.0543,0.0181];
a = [1.0000,-1.7600,1.1829,-0.2781];
m = 0:length(b)-1;
l = 0:length(a)-1;
k = 0:500;
w = (pi/500)*k;
nume = b * exp(-j * m' * w);
den = a * exp(-j * l' * w);
H = nume ./ den;
magH = abs(H);
angH = angle(H);
subplot(2,1,1);
plot(w/pi,magH);
title('Magnitude Response');
subplot(2,1,2);
plot(w/pi,angH);
title('Phase Response');
从图可以看出这确实是一个低通滤波器。