通俗易懂のAC自动机小结
AC自动机小结
AC自动机的思想 = trie树 + KMP
AC自动机是用来干什么的呢 多模式串匹配一个文本串
建成一个AC自动机需要三步
1. 构建trie树 2. 构建fail指针 3. 模式串匹配
首先用模式串建成一颗trie树 在每个模式串末尾打上标记 表示这是一个模式串的末尾
树上的每一个节点都对应一个fail指针 作用和KMP中的nex差不多
如果我可以通过fail指针走向一个节点 那么就表明新的这个节点到根节点的前缀字符串是我这个字符串中出现过的
可以直接从这个fail指针的节点继续匹配 大大节省了再匹配的时间
所以怎么建fail指针呢
首先fail指针指向的节点肯定与我当前节点代表的字符是一样的 (要不然怎么可以直接继续匹配呢)
其次要保证fail指向串的前缀在前一个模式串中出现过 要做到这一点 当前点的fail指针就要用到他父亲的fail指针来进行构建
具体看图
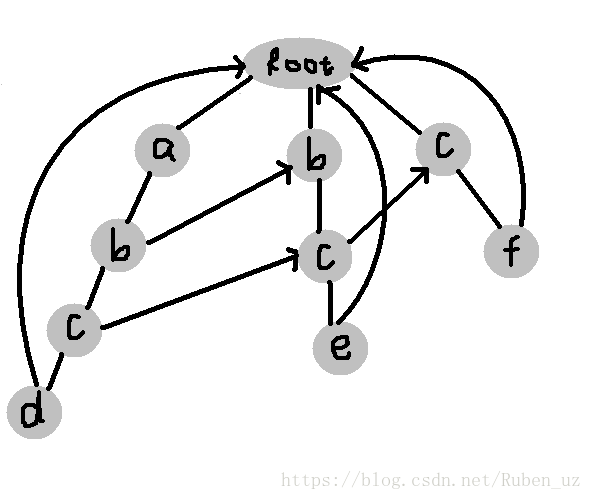
我现在有三个模式串 abcd bce cf 第一层的fail指针指向的都是root节点 那么从abcd开始看
abcd的b他的父亲a的fail是根节点 那么我们看他父亲的fail有没有指向和他相同的儿子
发现有bce中的b 直接指向那个b 同理 abcd中的c指向他父亲的fail的相同儿子c
这时候abcd中的d找不到相同的 就指向了root 这是fail的构建过程
但是我们发现一直沿着fail指针跳时间复杂度没办法完全保证 这时候就出现了trie图
简单地说就是 如果我没有这个儿子 我就把我fail的这个儿子扯下来做我的儿子 --和fail共享儿子
重新举个简单例子
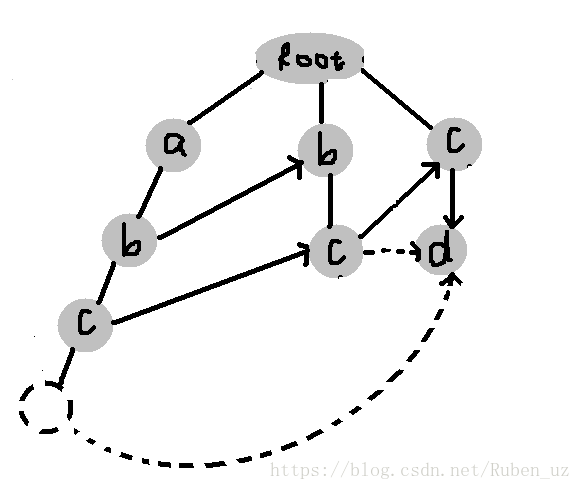
我现在有模式串 abc bc cd
图中的实边都是fail指针 现在我们来在此基础上优化成trie图 abc的c没有d这个儿子
但是他又很想要一个d儿子 怎么办呢 -- 就去他的fail的儿子里面找哇
(同样是fail因为要保证他fail那个串的前缀跟当前模板串相匹配)
但是他的fail也没有d这个儿子怎么办呢 他fail也是有fail的啊
这时候就指向了cd中的c了 太妙了 这个c有d这个儿子 这时候bc中的c就把cd中的d这下拉来当儿子了(虚边)
那么abc中的c就拉了bc的d来做儿子--也就cd的d儿子 这时候三个c共用一个d儿子
也就是说如果我的文本串是abcd 就走完abc后直接走向cd中的d了 直接保证了时间复杂度
这里有一个小细节 当我走到abc中的c时 他的fail(bc中的c)明明可以拉cd中的d下来做儿子
但是如果我bc中的c还没来得及拉儿子怎么办呢 会不会直接就指向根节点了吗?
答案是否定的 怎么避免这个问题呢
bfs就好了啊 我每次的fail指向的都是深度更浅的节点(想一想 为什么) 也就是说我在处理这个点时 我的fail已经在上层被处理过了
所以不会出现没来得及拉儿子的情况
AC自动机 美妙无比...!!
最最简单的板子(洛谷 P3808)
#include
#include
#include
#include
#include
using namespace std;
const int N = 500010;
int root = 0,cnt = 0,son[N][26],val[N],fail[N];
int n,ans;
char s[1000005],cmp[1000005];
queueq;
void ins(char * s) {
int len = strlen(s);
int now = root;
for(int i = 0;i < len;i ++) {
int v = s[i] - 'a';
if(! son[now][v]) son[now][v] = ++ cnt;
now = son[now][v];
}
val[now] ++;
}
void get_fail( ) {
for(int i = 0;i < 26;i ++)
if(son[root][i]) {
fail[son[root][i]] = root;
q.push(son[root][i]);
}
while(!q.empty( )) {
int u = q.front( ); q.pop( );
for(int i = 0;i < 26;i ++)
if(son[u][i]) {
q.push(son[u][i]);
fail[son[u][i]] = son[fail[u]][i];
}
else son[u][i] = son[fail[u]][i];
}
}
void get_ans(char * s) {
int len = strlen(s);
int now = root;
for(int i = 0;i < len;i ++) {
now = son[now][s[i] - 'a'];
for(int t = now;t && val[t] != -1;t = fail[t]) {
ans += val[t];
val[t] = -1;
}
}
}
int main( ) {
scanf("%d",& n);
for(int i = 1;i <= n;i ++) {
scanf("%s",s);
ins(s);
}
get_fail( );
scanf("%s",cmp);
get_ans(cmp);
printf("%d",ans);
return 0;
} 稍微复杂一点的板子 (洛谷 P3796)
#include
#include
#include
#include
#include
using namespace std;
queueQ;
const int N = 1e6 + 5;
const int M = 1e5 + 100;
char s[200][80],cmp[N];
int son[N][26],root = 0,cnt;
int ma,tim[N],n,fail[N],val[M];
void ins(char * s,int id) {
int len = strlen( s );
int now = root;
for(int i = 0;i < len;i ++) {
int v = s[i] - 'a';
if(! son[now][v]) son[now][v] = ++ cnt;
now = son[now][v];
}
val[now] = id;
}
void Get_fail( ) {
for(int i = 0;i < 26;i ++)
if(son[root][i]) {
Q.push(son[root][i]);
fail[son[root][i]] = root;
}
while(! Q.empty( )) {
int u = Q.front( );
Q.pop( );
for(int i = 0;i < 26;i ++) {
if(son[u][i]) {
fail[son[u][i]] = son[fail[u]][i];
Q.push(son[u][i]);
}
else son[u][i] = son[fail[u]][i];
}
}
}
void Get_ans(char * s) {
int now = root;
int len = strlen( s );
for(int i = 0;i < len;i ++) {
int v = s[i] - 'a';
for(int t = son[now][v];t;t = fail[t])
if(val[t]) tim[val[t]] ++;
now = son[now][v];
}
ma = tim[1];
for(int i = 1;i <= n;i ++)
if(ma < tim[i]) ma = tim[i];
}
void init( ) {
ma = 0; cnt = 0;
memset(son,0,sizeof(son));
memset(fail,0,sizeof(fail));
memset(tim,0,sizeof(tim));
memset(val,0,sizeof(val));
}
int main( ) {
while(scanf("%d",& n)) {
if(n == 0) break;
init( );
for(int i = 1;i <= n;i ++) {
scanf("%s",s[i]);
ins(s[i],i);
}
Get_fail( );
scanf("%s",cmp);
Get_ans( cmp );
printf("%d\n",ma);
for(int i = 1;i <= n;i ++)
if(tim[i] == ma) printf("%s\n",s[i]);
}
return 0;
} 写完小结后对AC自动机的理解更深了一层 大家也要加油哇...。