【论文解读】如何让CNN高效地在移动端运行

作者简介：SIGAI人工智能平台
全文PDF下载：http://www.tensorinfinity.com/paper_104.html

论文解读

COMPRESSION OF DEEP CONVOLUTIONAL NEURAL NETWORKS FOR FAST AND LOW POWER MOBILE APPLICATIONS【ICLR 2016】

尽管最新的高端智能手机有强大的CPU和GPU，但是在移动设备上运行复杂的深度学习模型（例如ImageNet分类模型）仍然十分困难。为了可以将深度网络模型应用于移动设备，本文提出了一个简单且有效的压缩整个CNN模型的方案，称为“one-shot whole network compression”，该方案包括三个步骤：a）利用VBMF（Variational Bayesian Matrix Factorization）选择合适的秩。b）对卷积核做Tucker分解。c）参数微调（fine-tune）恢复准确率。本文通过压缩各种CNN结构（AlexNet，VGG-S，GoogLeNet，VGG-16）证明了该方法的有效性。在很小的准确率损失下，可以极大地减少模型大小、运行时间和能量消耗。另外本文关于1*1卷积，提出了重要的实现方面的问题。

一．简介

最近，越来越多的工作关注与如何将CNN模型应用到移动端，在移动端的应用中，常用的方式是训练过程在服务器中进行，而测试或推断的过程则是在移动设备中执行。目前移动设备无法使用CNN模型的主要限制在于移动设备的存储能力，计算能力和电池供能。因此针对移动设备受限资源，需要单独设计CNN的结构。

众所周知，深度神经网络的参数是冗余的，而这也可以促使模型在训练中收敛到损失函数的一个不错的极小值点。那么为了提升模型在移动设备中测试过程的效率，我们可以对训练好的模型做处理，消除冗余的参数，同时对准确率没有明显的影响。目前有许多工作是利用低秩估计（视频中有介绍）来压缩CNN模型的【1，2，3】，而这些工作主要关注于卷积层，因为卷积层是所有层中最耗时的计算层。当前的许多工作尽管可以有效地压缩单层卷积，但是对整个网络的压缩仍然是一个待解决的挑战。

针对复杂任务（例如ImageNet的分类任务）训练得到的CNN模型，若要压缩整个模型仍然是很间距的任务，【4】工作提出可以使用“asymmetric 3d”的分解方法来加速所有的卷积层，另外他们也说明了选择有效秩的方法和优化的方法。尽管他们提出的方法可以在很多平台中实现（比如Caffe，Torch，Theano），但是秩的选择和优化的部分仍然需要额外的实现，本文则提出了一个更加简单且有效的方法，同样可以针对整个模型进行压缩，而且卷积层，全连接层都可以使用。

本文的主要创新和贡献在于：

1. 本文提出了“one-shot whole network compression scheme”，可以通过简单的三步（选择合适的秩、张量分解、模型调优）来实现对整个网络的压缩。

2. 在本文提出的方法中，利用Tucker分解的方法来做张量分解，利用VBMF（Variational Bayesian Matrix Fatorization）来做秩的估计。本文方法中每层的优化目标是最小化参数张量的重建误差，因此最后需要模型调优来保证准确率。

3. Tucker分解和VBMF都是可以利用开源的工具实现，而且模型调优也可以利用任意平台实现。

4. 本文针对多种CNN结构（AlexNet，VGG-S，GoogLeNet，VGG-16）在Titan X和智能手机上进行了压缩实验，证明了方法的有效性。

5. 通过分析功率消耗，本文发现了关于11卷积核操作的现象，即尽管11卷积是很简单的操作，但是由于没有有效的缓存存储，这类卷积层是理论加速率和实际加速率不一致的主要原因。

二．相关工作

CNN模型的压缩

CNN模型中最常见的是卷积层和全连接层，相应的卷积层主导了计算的时间，全连接层主导了模型的大小。【5】受限提出神经网络中删除冗余参数的可能，并且提出了几种模型压缩的技术。后来怕【2】提出可以使用SVD分解来压缩全连接层的参数矩阵，同时可以保证准确率没有太大的下降。最近更多的方法被探索，【6】基于向量量化，【7】基于哈希技术，【8】利用循环投影，都可以压缩CNN模型，【9】利用张量分解的方法提出了比SVD压缩效果更好的方法。【2，1】基于低秩分解的方法，针对卷积层的参数进行压缩，但是他们都仅仅对单层卷积或几层卷积做压缩，并没有应用于深度网络中。

最近【4】提出“asymmetric 3d” 分解的方法可以压缩整个网络。他们提出原本DD的卷积可以分解为D1，1D和11的卷积，此外，他们也提出使用PCA来估计张量的秩，已经通过最小化非线性层输出特征图的重建误差来得到分解后的参数张量（卷积核），最后他们也提出未来改进中可以使用参数调优（fine-tune）来进一步保证准确率。本文提出的方法与上述方法的不同之处在于，本文利用Tucker分解，可以压缩卷积层和全连接层，利用VBMF来做张量秩的估计，并通过最小化参数张量的重建误差来获得压缩后的参数张量。

张量分解

张量本质上是多维的数组，例如向量可以看作1维张量，矩阵是2维张量。两个最常见的张量分解方法是CP分解【10,11,12】和Tucker分解【13,14,15】，本文利用的是Tucker分解。Tucker分解可以看作是一个高阶的SVD分解，对于全连接层的Tucker分解就等同于SVD分解，即针对卷积层做Tucker分解，针对全连接层做SVD分解。对于第一层卷积，由于输入通道数很小（彩图为3）因此也是做SVD分解，具体的流程如图2.1所示
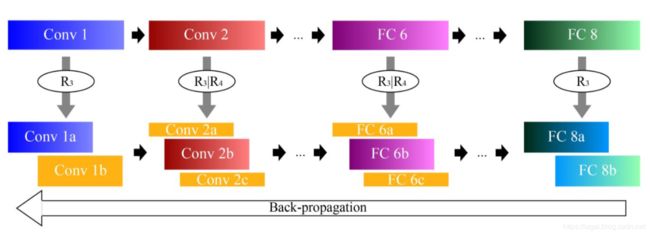图2.1 本文提出的低秩估计方法

三．本文方法

如图2.1所示为本文提出方法的流程，压缩整个网络包括三个步骤：1）选择合适的秩；2）Tucker分解；3）参数调优。在第一步中，本文利用VBMF分析参数张量，并得到合适的秩；接着使用Tucker分解针对每一层做压缩，每个张量保留的秩就是VBMF得到的秩；最后利用BP（back propagation）做参数调优。

Tucker分解

在CNN中，我们不考虑batch那一维，那么实际卷积的输入张量，卷积核和输出张量设为$X$，$K$，$Y$
$$X\in {\mathbb{R}}^{H\ast W\ast S},K\in {\mathbb{R}}^{S\ast D\ast D\ast T},Y\in {\mathbb{R}}^{H^{\prime }\ast W^{\prime }\ast T}$$
则卷积层的操作可以通过如下公式获得，式中$\Delta$为stride，$P$为padding的大小
$$y_{h^{\prime },w^{\prime },t}=\sum _{i=1}^D\sum _{j=1}^D\sum _{s=1}^S{K}_{i,j,s,t}{X}_{h_i{w}_{j}s}$$
$$h_i=(h^{\prime }-1)\Delta +i-P,w_j=(w^{\prime }-1)\Delta +j-P$$

如果我们以秩$(R_1,R_2,R_3,R_4)$做Tucker分解，那么卷积核参数可以估计表示为如下形式，式中为核张量，$U^1,U^2,U^3,U^4$为参数矩阵

对于我们实际CNN中的模型，我们不用对所有维度做分解，比如第2，3维，实际上对应与空间维度$(D\ast D)$本身很小不需要压缩，因此实际应用的对参数张量的估计为下式，式中$C$为核张量

$$K_{i,j,s,t}=\sum _{r_3=1}^{R_3}\sum _{r_4=1}^{R_4}{C}_{i,j,r_3,r_4{U}_{s,r_3}^3{U}_{t,r_4}^4}$$
$$C\in {\mathbb{R}}^{D\ast D\ast R_3\ast R_4}$$
我们将卷积公式中的参数张量用估计的张量来表示，于是得到以下的计算公式，式中$Z$,$Z^{\prime }$都是临时张量，而下式中的每一步都可以用卷积来实现。
$$Z_{h,w,r_3}=\sum _{s=1}^s{U}_{s,r_3}^3{X}_{h,w,s}$$
$$Z_{h^{\prime }{w}^{\prime },r_4}^{\prime }=\sum _{i=1}^D\sum _{j=1}^D\sum _{r_3=1}^{R_3}{C}_{r_1,r_2,r_4}{Z}_{h_i,w_j,r_3}$$
$$y_{h^{\prime }{w}^{\prime },t}^{\prime }=\sum _{r_4=1}^{R_4}{U}_{t,r_4}^4{Z}_{h^{\prime },w^{\prime },r_4}^{\prime }$$
$$Z\in {\mathbb{R}}^{H\ast W\ast R_3},Z^{\prime }\in {\mathbb{R}}^{H^{\prime }\ast W^{\prime }\ast R_4}$$
分解后的卷积过程如图3.1所示，首先是$1\ast 1$的卷积，可以看作通道维度的压缩，第二个卷积是$D\ast D$的卷积，可以看作是做空间维度的信息交流，最后一个卷积是$1\ast 1$的卷积，可以看作是将通道维度还原。

图3.1 Tucker分解后的卷积操作

从上图中，我们可以看到第一个卷积和第三个卷积都是$1\ast 1$的卷积核，本质上是对于输入特征图$X$做了通道维度的线性重组，这个方法与【16】提出的“network-in-network”很相似，而且这种结构也广泛应用与CNN模型中（比如GoogLeNet中的Inception结构），但是本文提出的结构与之最大的不同在于，第一个和第二个卷积之后并没有加非线性层。

复杂度分析
原本的卷积操作，需要个参数，“multiplication-addition”操作数为（即乘法-加法操作，$1$个乘法-加法操作数是$1$个乘法和1个加法操作。由于卷积，矩阵乘法都可以归结为向量内积，而向量内积操作中乘法个数=加法个数$-1$，当向量维度很大时，两者基本可看作相等，于是在CNN计算操作数通常使用乘法-加法操作数来衡量），因此通过Tucker分解，每层卷积的压缩率和加速率可以表示为

$$M=\frac{D^{2}ST}{S{R}_3+D^2{R}_3{R}_4+T{R}_4}$$
$$E=\frac{D^{2}ST{H}^{\prime }{W}^{\prime }}{S{R}_{3}HW+D^2{R}_3{H}^{\prime }{W}^{\prime }+T{R}_4{H}^{\prime }{W}^{\prime }}$$

从上式我们可以看到秩$R_3$,$R_4$是非常重要的超参数，他们决定了压缩率和加速率，同时也极大影响着准确率。而秩的估计本身又是十分困难的，本文利用了VBMF来做秩的估计，主要参考是【17】

CP分解与Tucker分解的对比

CP分解实际上将张量转化为若干1维向量乘积的和，如图3.2所示

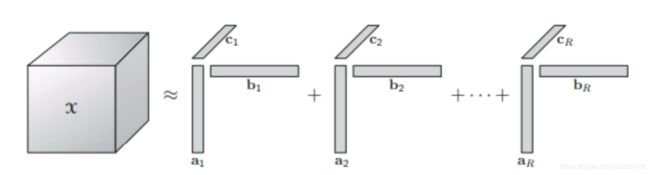
图3.2 CP分解
【2，3】使用了CP分解来估计卷积层的参数，但是工作中仅针对8层网络进行了实验。实际上CP分解的稳定性略差于Tucker，而且其计算更加耗时。而本文通过大量的实验证明了Tucker分解可以有效地压缩AlexNet，VGG-S，GoogLeNet，VGG-16等网络。

参数调优

由于本文提出的方法是最小化参数张量的重建误差，（asymmetric 3d方法中是最小化特征图的重建误差）因此直接做Tucker分解后模型的准确率会有很大程度的降低（在作者的试验中，AlexNet压缩后会有50%的准确率损失）。图3.3为参数调优的实验，横坐标为训练迭代次数，纵坐标为ImageNet Top-5准确率。通过实验可以发现，参数调优可以很容易地恢复模型地准确率，而且仅经过1Epoch的迭代就可以将模型准确率恢复到不错的效果。

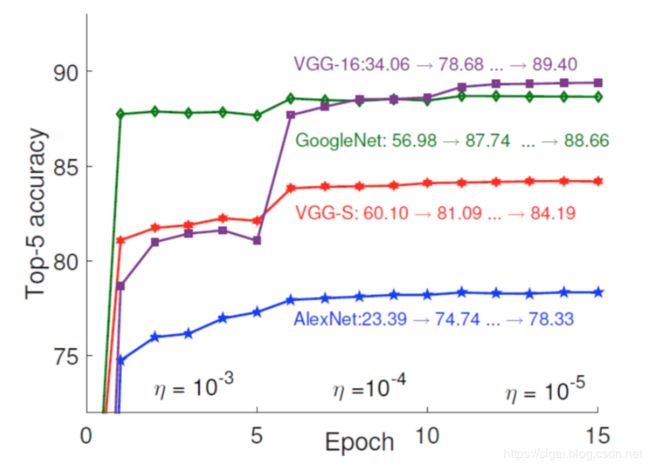
图3.3 参数调优对准确率的影响

在作者的实验中，设定基本学习率是$0.001$，之后每5Epoch或10Epoch降为之前的$0.1$。同时为了证明Tucker分解的有效性，作者按照分解后的网络结构，以高斯随机分布初始化网络参数从头训练，发现得到的模型效果并不好，由此可以证明Tucker分解获得分解后的参数是必要的。

四．相关实验

首先作者利用4个有代表性的网络来验证方法的有效性：AlexNet，VGG-S，GoogLeNet，VGG-16。针对每一个网络，作者都在Nvidia Titan X和智能手机 Samsung Galaxy S6上进行了对比实验。其次作者针对AlexNet进行逐层的压缩效果分析。最后作者也测量了在智能手机上运行时的功率消耗（包括GPU和内存的功率消耗）

整体压缩结果

图4.1为针对四种不同网络，在Titan X和Samsung Galaxy S6上的效果，图中*表示经过压缩后的网络。 实验发现本文提出的方法可以针对不同的网络达到很好的压缩和加速效果，在Titan X上可以达到$1.23$ ~ $2.33$的加速效果，而在移动设备上也可以达到$1.42$~$3.68$的加速效果。

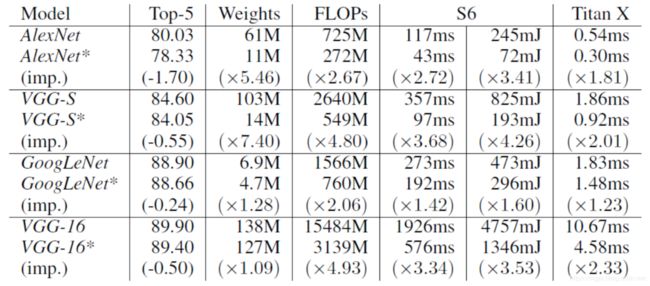
图4.1 针对各个网络的压缩和加速效果

经过实验，作者发现移动设备中加速的效果明显由于GPU的加速效果。作者分析主要原因在于移动设备中GPU去我少线程级的并行计算，Samsung S6中的县城数比Titan X少24倍。模型经过压缩，可以将整个参数个数大大减少，同时就减少了缓存的占用和内存的读取数据的时间。而这种优势在缺少并行线程的GPU中体现得更加明显。

逐层压缩结果

图4.2为针对AlexNet的逐层压缩和加速的效果分析，对图中每一层，上面的结果为原网络的结果，下面的结果为经过压缩后网络的结果。经过Tucker分解后，每一个卷积实际分解成了三个矩阵的乘法（在实现中矩阵乘法有卷积代替）,作者在结果中也显示了每个矩阵乘法的运算量(在分解后模型的FLOPs中括号中的三个数分别代表3个矩阵乘法的运算量)。

经过实验，作者发现在移动设备上，全连接层的加速效果由于卷积层。作者分析同样是由于参数减少，缓解了缓存的压力，而全连接层的参数个数远远多于卷积层，而且卷积层的参数有很大程度的共享，全连接层的参数都仅利用了一次，因此这种优势也更加明显。对于全连接层这种参数仅利用一次的数据，被称为“dead-on-arrival(DoA) data”，就缓存而言，DoA数据相比于卷积层是低效的。因此全连接层的加速效果会明显由于卷积层。
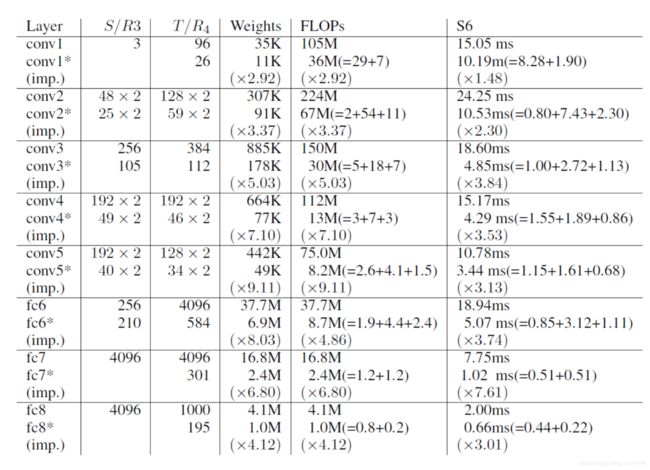图4.2 针对AlexNet的逐层压缩和加速效果分析

功耗

由于VGG-16网络与VGG-S网络有相同的趋势，因此作者仅以VGG-S的结果来表示VGG网络结构在压缩前后的功率。结果如图4.3所示。

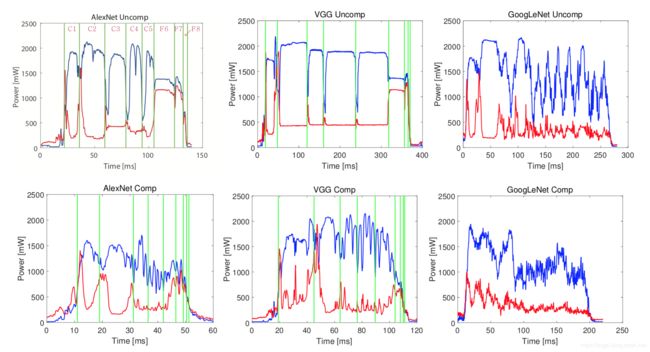
图4.3 本文方法对功率消耗的影响

每个图表示相应网络的功率随时间的变化情况，图中蓝色曲线表示GPU的功率，红色的曲线表示内存的功率。经过实验发现压缩后网络的功耗低于原网络，作者分析是由于大量利用11卷积的结果。在平台执行卷积操作时，会有相应的优化技术（比如Caffeinated convolution）在这样的情况下，11的卷积相比于其他卷积（33或55等）对缓存的利用率更低，因为数据的重复利用量与卷积层的参数个数成正比。所以计算11卷积时会发生更多的缓存未命中问题（cache miss），而缓存未命中情况发生时，会导致GPU空闲而减少功耗，所以在执行11卷积时，GPU的功耗会下降，但同样也会导致GPU功耗的震荡。在原网络中GPU的功耗在每一层中都是比较平稳的（GoogLeNet中由于其结构本身就大量使用1*1卷积，因此原网络GPU功耗也有震荡的情况）但实际上，这种GPU空闲和缓存未命中的情况是低效的。

参考文献

[1]. Jaderberg, M., Vedaldi, A., and Zisserman, A. Speeding up convolutional neural networks with low rank expansions. In British Machine Vision Conference, 2014.

[2]. Denton, Emily L, Zaremba, Wojciech, Bruna, Joan, LeCun, Yann, and Fergus, Rob. Exploiting linear structure within convolutional networks for efficient evaluation. In Advances in Neural Information Processing Systems, pp. 1269–1277, 2014.

[3]. Lebedev, Vadim, Ganin, Yaroslav, Rakhuba, Maksim, Oseledets, Ivan, and Lempitsky, Victor. Speeding-up convolutional neural networks using fine-tuned cp-decomposition. In International Conference on Learning Representations, 2015.

[4]. Zhang, Xiangyu, Zou, Jianhua, Ming, Xiang, He, Kaiming, and Sun, Jian. Efficient and accurate approximations of nonlinear convolutional networks. 2015b.

[5]. Denil, Misha, Shakibi, Babak, Dinh, Laurent, de Freitas, Nando, et al. Predicting parameters in deep learning. In Advances in Neural Information Processing Systems, pp. 2148–2156, 2013.

[6]. Gong, Yunchao, Liu, Liu, Yang, Ming, and Bourdev, Lubomir. Compressing deep convolutional networks using vector quantization. arXiv preprint arXiv:1412.6115, 2014.

[7]. Chen,Wenlin,Wilson, James T, Tyree, Stephen,Weinberger, Kilian Q, and Chen, Yixin. Compressing neural networks with the hashing trick. arXiv preprint arXiv:1504.04788, 2015.

[8]. Cheng, Yu, Yu, Felix X, Feris, Rogerio S, Kumar, Sanjiv, Choudhary, Alok, and Chang, Shih-Fu. Fast neural networks with circulant projections. arXiv preprint arXiv:1502.03436, 2015.

[9]. Novikov, Alexander, Podoprikhin, Dmitry, Osokin, Anton, and Vetrov, Dmitry. Tensorizing neural networks. arXiv preprint arXiv:1509.06569, 2015.

[10].Carroll, J Douglas and Chang, Jih-Jie. Analysis of individual differences in multidimensional scaling via an n-way generalization of eckart-young decomposition. Psychometrika, 35(3):283–319,1970.

[11].Harshman, Richard A and Lundy, Margaret E. Parafac: Parallel factor analysis. Computational Statistics & Data Analysis, 18(1):39–72, 1994.

[12]. Shashua, Amnon and Hazan, Tamir. Non-negative tensor factorization with applications to statistics and computer vision. In Proceedings of the 22nd international conference on Machine learning, pp. 792–799. ACM, 2005.

[13].Tucker, Ledyard R. Some mathematical notes on three-mode factor analysis. Psychometrika, 31(3): 279–311, 1966.

[14]. De Lathauwer, Lieven, De Moor, Bart, and Vandewalle, Joos. A multilinear singular value decomposition. SIAM journal on Matrix Analysis and Applications, 21(4):1253–1278, 2000.

[15]. Kim, Y.-D. and Choi, S. Nonnegative Tucker decomposition. In Proceedings of the IEEE CVPR-2007 Workshop on Component Analysis Methods, Minneapolis, Minnesota, 2007.

[16]. Lin, M., Chen, Q., and Yan, S. Network in network. In International Conference on Learning Representations, 2014.

[17]. Nakajima, Shinichi, Sugiyama, Masashi, Babacan, S Derin, and Tomioka, Ryota. Global analytic solution of fully-observed variational bayesian matrix factorization. The Journal of Machine Learning Research, 14(1):1–37, 2013.