Numpy课后习题
Numpy课后习题
Generate matrices A, with random Gaussian entries, B, a Toeplitz matrix,where A ∈Rn×m and B ∈Rm×m, for n = 200, m = 500.
由于n = 200, m = 500过大,难以显示,使用n = 10, m = 15替代
1.类的创建和初始化,创建矩阵A、B,A矩阵利用randn生成高斯分布的元素值,B矩阵利用toeplitz函数生成toeplitz矩阵
import numpy as np
import numpy.matlib as npm
import numpy.linalg as npl
from scipy.linalg import toeplitz
import scipy
import time
import random
import math
class Exercise():
def __init__(self):
self.n = 10
self.m = 15
t = npm.rand(1, self.m)
self.A = npm.randn(self.n, self.m)
self.B = toeplitz(t)
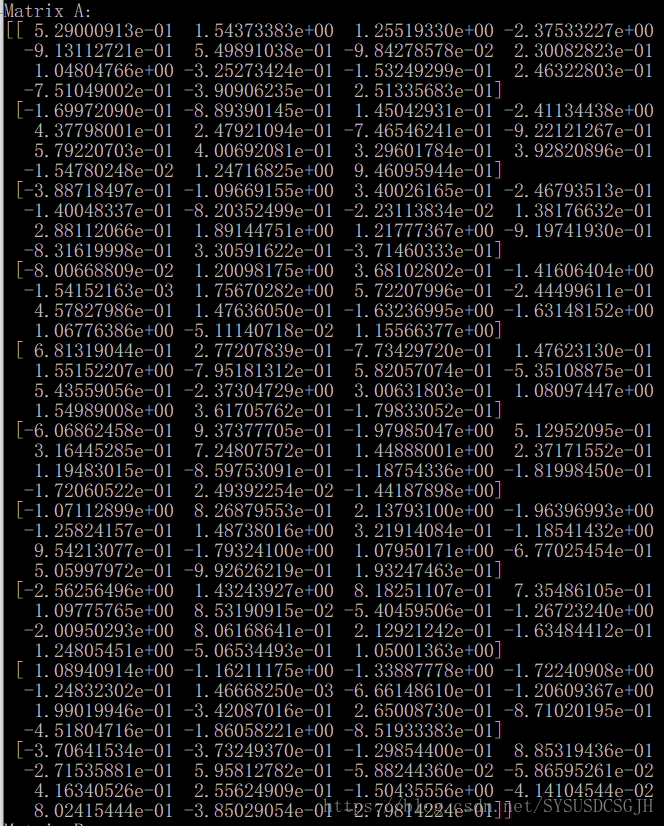
print("Matrix A:")
print(self.A)
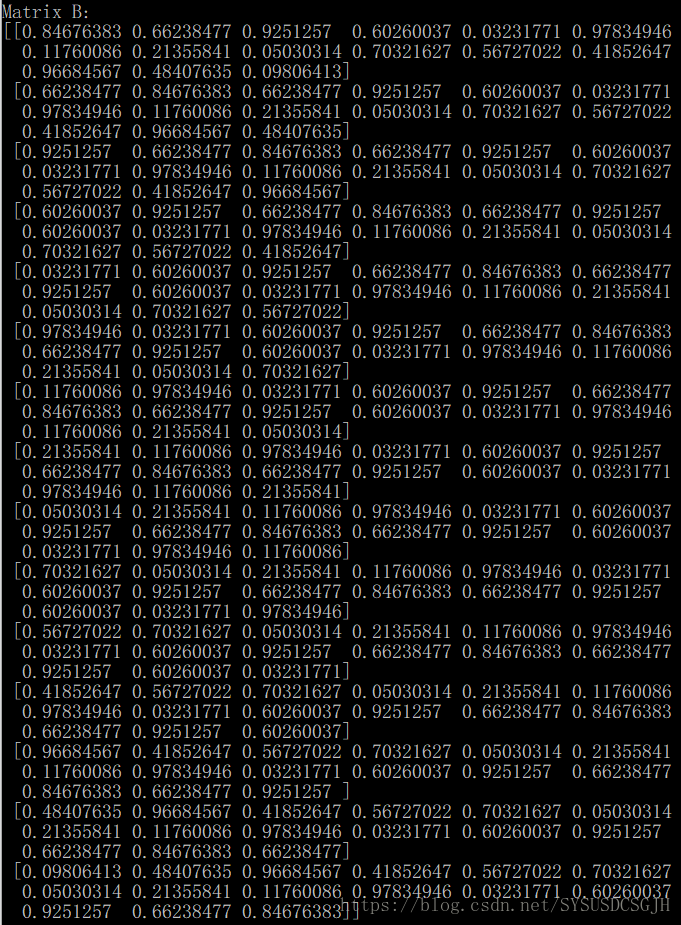
print("Matrix B:")
print(self.B)
print()2、Exercise 9.1:Calculate A + A, AAT,ATA and AB. Write a function that computes A(B−λI) for any λ.
做法:直接调用其内置的函数,实现加法和内乘。使用属性T获取转置矩阵。
def Exercise_9_1(self, k):
"""
Exercise 9.1:Calculate A + A, AAT,ATA and AB.
Write a function that computes A(B−λI) for any λ.
"""
print("Exercise_9_1")
print("A + A")
print(self.A + self.A)
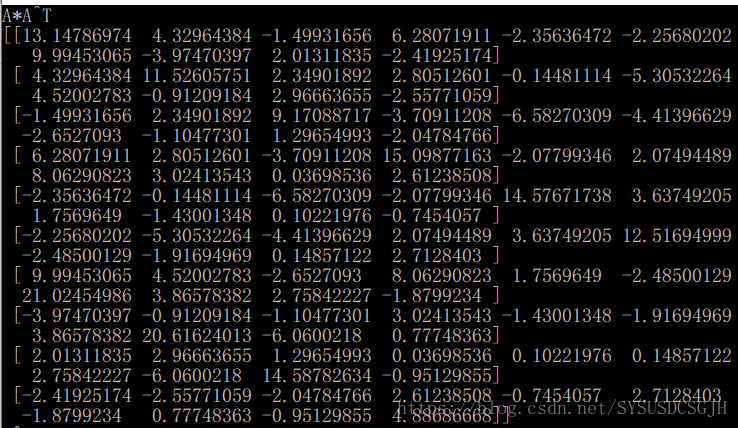
print("A*A^T")
print(self.A * self.A.T)
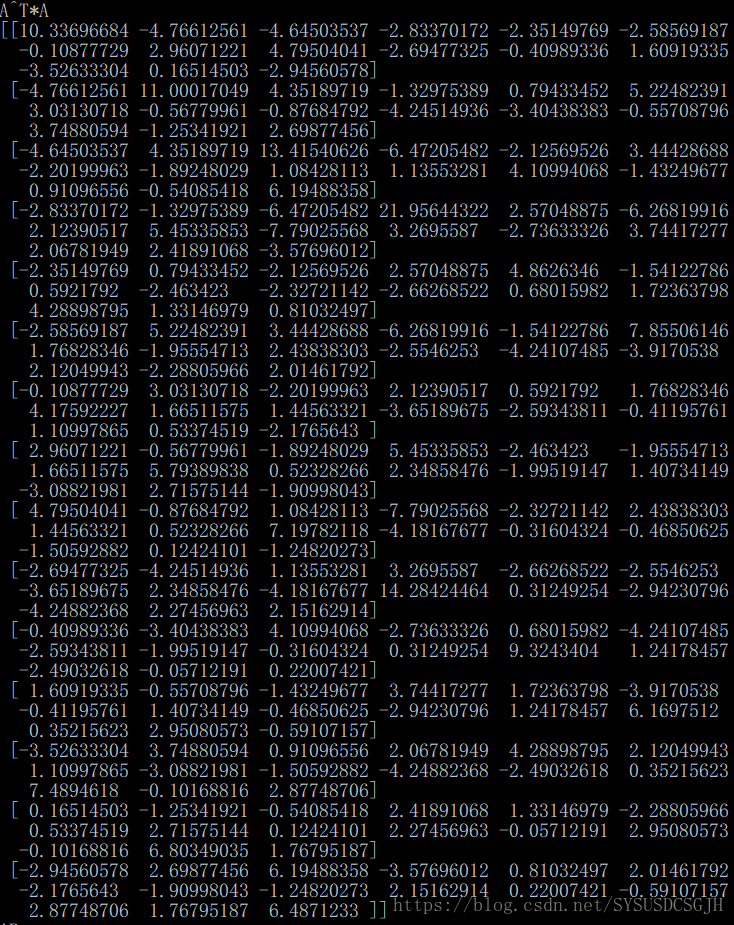
print("A^T*A")
print(self.A.T * self.A)
print("AB")
print(self.A * self.B)
print("A(B-kI) for k = " + str(k))
print(self.A * (self.B - k * npm.identity(self.m)))
print()3、Exercise 9.2:Generate a vector b with m entries and solve Bx = b.
做法:使用rand随机生成b矩阵,利用numpy.linalg.solve求解Bx=b得到x,最后带入Bx与b比较是否相等验证结果。
def Exercise_9_2(self):
"""
Exercise 9.2:Generate a vector b with
m entries and solve Bx = b.
"""
print("Exercise_9_2")
b = npm.rand(self.m, 1)
print("matrix b")
print(b)
x = npl.solve(self.B, b)
print("x for B*x = b")
print(x)
print("nunpy.allclose(self.B * x, b) = " +
str(np.allclose(self.B * x, b)))
print()4、Exercise 9.3:Compute the Frobenius norm of A: ||A||F and the infinity norm of B: ||B||∞. Also find the largest and smallest singular values of B.
做法:使用norm和eigvals函数求解范数和特征值。
def Exercise_9_3(self, F):
"""
Exercise 9.3:Compute the Frobenius norm of A: ||A||F and the
infinity norm of B: ||B||∞. Also find the largest
and smallest singular values of B.
"""
print("Exercise_9_3")
print("||A||F : " + str(npl.norm(self.A, F)))
print("||B||∞ : " + str(npl.norm(self.B, np.inf)))
beig = npl.eigvals(self.B)
print("Max eigval of B : " + str(max(beig)))
print("Min eigval of B : " + str(min(beig)))
print()5、Exercise 9.4:Generate a matrix Z, n × n, with Gaussian entries, and use the power iteration to find the largest eigenvalue and corresponding eigenvector of Z. How many iterations are needed till convergence?
做法:根据幂法求解的过程写成python代码,输出结果
def Exercise_9_4(self, n):
"""
Exercise 9.4:Generate a matrix Z, n × n, with Gaussian entries,
and use the power iteration to find the largest eigenvalue and
corresponding eigenvector of Z. How many iterations are needed
till convergence?
Optional: use the time.clock() method to compare computation
time when varying n.
"""
print("Exercise_9_4")
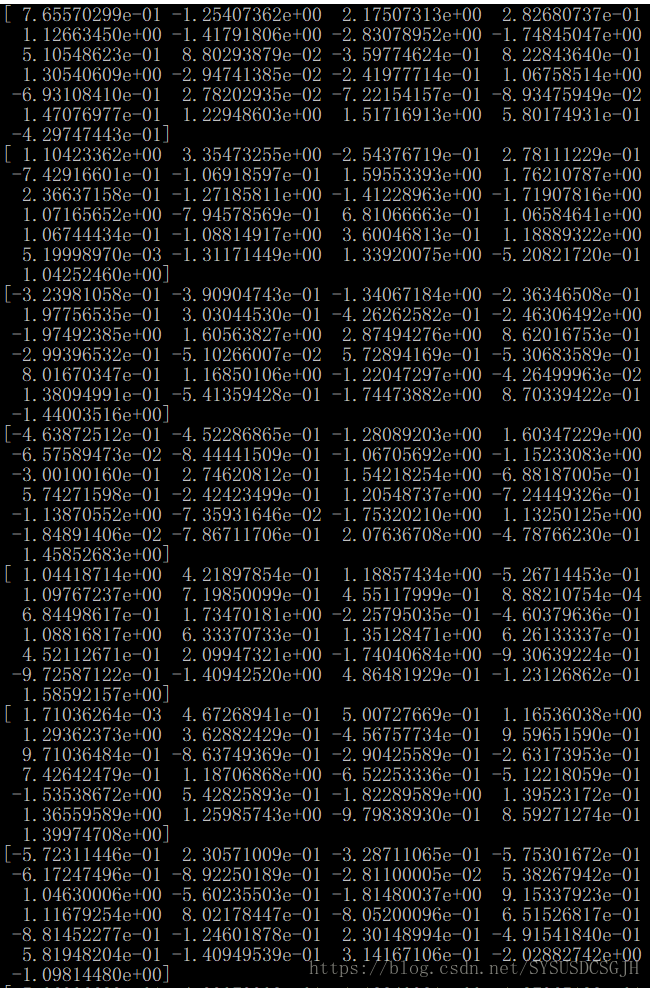
tstart = time.clock()
Z = npm.randn(n, n)
u = npm.rand(n, 1)
k1 = 0
k2 = 1
count = 0
print("Matrix Z:")
print(Z)
while math.fabs(k1 - k2) > 1e-10:
count = count + 1
v = Z * u
k1 = k2
k2 = max(np.abs(v))
u = v / k2
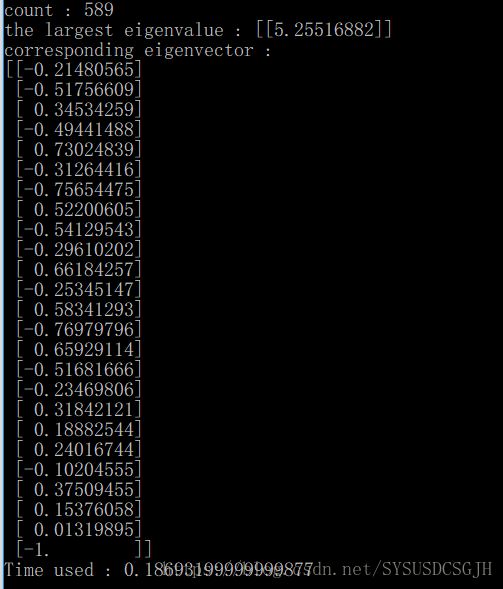
print("count : " + str(count))
print("the largest eigenvalue : " + str(count))
tend = time.clock();
print("Time used : " + str(tend - tstart))
print()对于n=25,迭代了589次,用了0.19s的时间。
6、Exercise 9.5 Generate an n×n matrix, denoted by C, where each entry is 1 with probability p and 0 otherwise. Use the linear algebra library of Scipy to compute the singular values of C. What can you say about the relationship between n, p and the largest singular value?
做法:利用random.random()生成[0,1)的浮点数与p比较,小于p则该位置为1,否则为0,据此生成C矩阵,用svd分解函数scipy.linalg.svd得到s
def Exercise_9_5(self, n, p):
"""
Generate an n×n matrix, denoted by C, where each entry is 1 with
probability p and 0 otherwise. Use the linear algebra library of
Scipy to compute the singular values of C.
What can you say about the relationship between n, p
and the largest singular value?
"""
print("Exercise_9_5")
C = npm.zeros((n, n))
for i in range(0, n):
for j in range(0, n):
if random.random() < p:
C[i,j] = 1
(u,s,v) = scipy.linalg.svd(C)
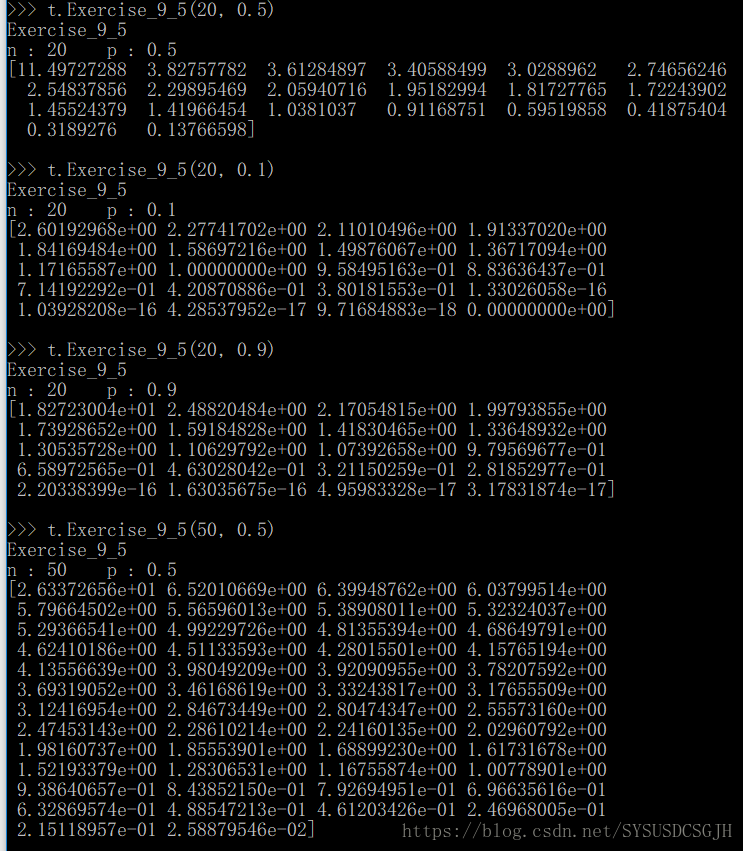
print("n : " + str(n) + " p : " + str(p))
print(s)
print()p越接近0.5,其奇异值越大。
7、Exercise9.6Write a function that takes a value z and an array A and finds the element in A that is closest to z. The function should return the closest value, not index.
Hint: Use the built-in functionality of Numpy rather than writing code to find this value manually. In particular, use brackets and argmin.
做法:先得到差值矩阵A-z,将矩阵内元素取绝对值,元素则表示z到A矩阵该位置元素的距离,再利用numpy.argmin函数得到最小值下标,再取元素值则为答案。
def Exercise_9_6(self, A, z):
"""
Write a function that takes a value z and an array A and finds
the element in A that is closest to z. The function should
return the closest value, not index.
Hint: Use the built-in functionality of Numpy rather than
writing code to find this value manually. In particular,
use brackets and argmin.
"""
print("Exercise_9_6")
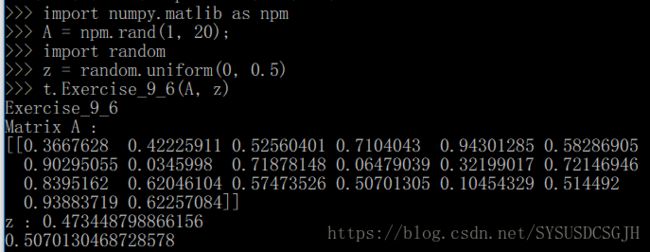
print("Matrix A :")
print(A)
print("z : " + str(z))
print(A[0, np.argmin(np.abs(A-z))])
print()