图像算法之七：特征提取算法之LBP

     【2016/9/29】今天重点学习了纹理特征提取算法LBP,这个算法可以用于纹理特征提取和人脸识别，应用比较广泛。首先介绍LBP算法的原理，然后是LBP特征的提取步骤，最后使用OpenCV实现了这个算法。    

   LBP（Local Binary Pattern，局部二值模式）是一种用来描述图像局部纹理特征的算子；它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出，用于纹理特征提取。而且，提取的特征是图像的局部的纹理特征。

1、LBP特征的描述

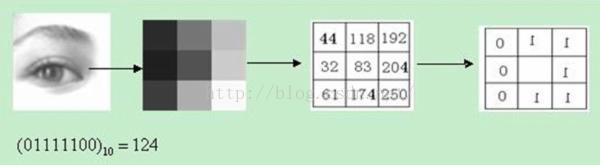
原始的LBP算子定义为在3*3的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素 点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数（通常转换为十进制数即LBP码，共256种），即得到该窗口中心像 素点的LBP值，并用这个值来反映该区域的纹理信息。如下图所示：

LBP的改进版本：

原始的LBP提出后，研究人员不断对其提出了各种改进和优化。

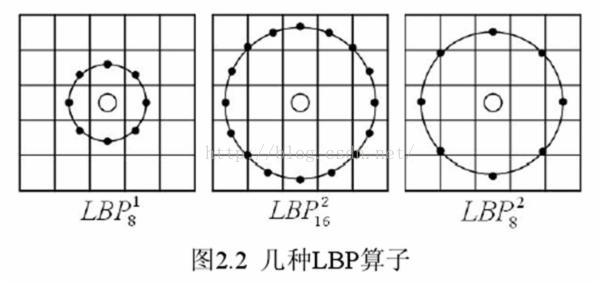
（1）圆形LBP算子：

基本的 LBP算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征，并达到灰度和旋 转不变性的要求，Ojala等对 LBP 算子进行了改进，将 3×3邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的 LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子。

（2）LBP旋转不变模式

从 LBP 的定义可以看出，LBP 算子是灰度不变的，但却不是旋转不变的。图像的旋转就会得到不同的 LBP值。

Maenpaa等人又将 LBP算子进行了扩展，提出了具有旋转不变性的 LBP 算子，即不断旋转圆形邻域得到一系列初始定义的 LBP值，取其最小值作为该邻域的 LBP 值。

图 2.5 给出了求取旋转不变的 LBP 的过程示意图，图中算子下方的数字表示该算子对应的 LBP值，图中所示的 8 种 LBP模式，经过旋转不变的处理，最终得到的具有旋转不变性的 LBP值为 15。也就是说，图中的 8种 LBP 模式对应的旋转不变的 LBP模式都是00001111。

（3）LBP等价模式

    一个LBP算子可以产生不同的二进制模式，对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生P  2 种模式。很显然，随着邻域集内采样点数的增加，二进制模式的种类是急剧增加的。例如：5×5邻域内20个采样点，有2  20 ＝1,048,576种二进制模式。如此多的二值模式无论对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。同时，过多的模式种类对于纹理 的表达是不利的。例如 ，将LBP算子用于纹理分类或人脸识别时，常采用LBP模式的统计直方图来表达图像的信息，而较多的模式种类将使得数据量过大，且直方图过于稀疏。因此，需要对原始的LBP模式进行降维，使得数据量减少的情况下能最好的代表图像的信息。

为了解决二进制模式过多的问题，提高统计性，Ojala提出了采用一种“等价模式”（Uniform Pattern）来对LBP算子的模式种类进行降维。Ojala等认为，在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因 此，Ojala将“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式 类。如00000000（0次跳变），00000111（只含一次从0到1的跳变），10001111（先由1跳到0，再由0跳到1，共两次跳变）都是等 价模式类。除等价模式类以外的模式都归为另一类，称为混合模式类，例如10010111（共四次跳变）

通过这样的改进，二进制模式的种类大大减少，而不会丢失任何信息。模式数量由原来的2 P 种减少为 P ( P-1)+2种，其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说，二进制模式由原始的256种减少为58种，这使得特征向量的维数更少，并且可以减少高频噪声带来的影响。

2、LBP特征用于检测的原理

显而易见的是，上述提取的LBP算子在每个像素点都可以得到一个LBP“编码”，那么，对一幅图像（记录的是每个像素点的灰度值）提取其原始的LBP算子之后，得到的原始LBP特征依然是“一幅图片”（记录的是每个像素点的LBP值）。

LBP的应用中，如纹理分类、人脸分析等，一般都不将LBP图谱作为特征向量用于分类识别，而是采用LBP特征谱的统计直方图作为特征向量用于分类识别。

因为，从上面的分析我们可以看出，这个“特征”跟位置信息是紧密相关的。直接对两幅图片提取这种“特征”，并进行判别分析的话，会因为“位置没有对准”而产生很大的误差。后来，研究人员发现，可以将一幅图片划分为若干的子区域，对每个子区域内的每个像素点都提取LBP特征，然后，在每个子区域内建立LBP特征的统计直方图。如此一来，每个子区域，就可以用一个统计直方图来进行描述；整个图片就由若干个统计直方图组成；

例如：一幅100*100像素大小的图片，划分为10个子区域（可以通过多种方式来划分区域），每个子区域的大小为10*10像 素；在每个子区域内的每个像素点，提取其LBP特征，然后，建立统计直方图；这样，这幅图片就有10个子区域，也就有了10个统计直方图，利用这10个统计直方图，就可以描述这幅图片了。之后，我们利用各种相似性度量函数，就可以判断两幅图像之间的相似性了；

3、对LBP特征向量进行提取的步骤

（1）首先将检测窗口划分为16×16的小区域（cell）；

（2）对于每个cell中的一个像素，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数，即得到该窗口中心像素点的LBP值；

（3）然后计算每个cell的直方图，即每个数字（假定是十进制数LBP值）出现的频率；然后对该直方图进行归一化处理。

（4）最后将得到的每个cell的统计直方图进行连接成为一个特征向量，也就是整幅图的LBP纹理特征向量；

然后便可利用SVM或者其他机器学习算法进行分类了。

4、LBP算法实现

Language: C++(OpenCV)

#include "opencv2/core/core.hpp"
#include "opencv2/contrib/contrib.hpp"
#include "opencv2/highgui/highgui.hpp"

#include 
#include 
#include 

using namespace cv;
using namespace std;

void elbp(Mat& src, Mat &dst, int radius, int neighbors)
    {

    for(int n=0; n(-radius * sin(2.0*CV_PI*n/static_cast(neighbors)));
        float y = static_cast(radius * cos(2.0*CV_PI*n/static_cast(neighbors)));
        // 上取整和下取整的值
        int fx = static_cast(floor(x));
        int fy = static_cast(floor(y));
        int cx = static_cast(ceil(x));
        int cy = static_cast(ceil(y));
        // 小数部分
        float ty = y - fy;
        float tx = x - fx;
        // 设置插值权重
        float w1 = (1 - tx) * (1 - ty);
        float w2 =      tx  * (1 - ty);
        float w3 = (1 - tx) *      ty;
        float w4 =      tx  *      ty;
        // 循环处理图像数据
        for(int i=radius; i < src.rows-radius;i++)
            {
            for(int j=radius;j < src.cols-radius;j++) 
                {
                // 计算插值
                float t = static_cast(w1*src.at(i+fy,j+fx) + w2*src.at(i+fy,j+cx) + w3*src.at(i+cy,j+fx) + w4*src.at(i+cy,j+cx));
                // 进行编码
                dst.at(i-radius,j-radius) += ((t > src.at(i,j)) || (std::abs(t-src.at(i,j)) < std::numeric_limits::epsilon())) << n;
                }
            }
        }
    }

void elbp1(Mat& src, Mat &dst)
    {

        // 循环处理图像数据
        for(int i=1; i < src.rows-1;i++)
            {
            for(int j=1;j < src.cols-1;j++) 
                {
                uchar tt = 0;
                int tt1 = 0;
                uchar u = src.at(i,j);
                if(src.at(i-1,j-1)>u) { tt += 1 <(i-1,j)>u) { tt += 1 <(i-1,j+1)>u) { tt += 1 <(i,j+1)>u) { tt += 1 <(i+1,j+1)>u) { tt += 1 <(i+1,j)>u) { tt += 1 <(i+1,j-1)>u) { tt += 1 <(i-1,j)>u) { tt += 1 <(i-1,j-1) = tt;// 更正，之前是dst.at(i,j)=tt;
                }
            }
        }

int main()
    {
    Mat img = cv::imread("bear.jpg", 0);
    namedWindow("image");
    imshow("image", img);

    int radius, neighbors;
    radius = 1;
    neighbors = 8;

    //创建一个LBP图谱
    Mat dst = Mat(img.rows-2*radius, img.cols-2*radius,CV_8UC1, Scalar(0));
    elbp1(img,dst);
    namedWindow("normal");
    imshow("normal", dst);

    Mat dst1 = Mat(img.rows-2*radius, img.cols-2*radius,CV_8UC1, Scalar(0));
    elbp(img,dst1,1,8);
    namedWindow("circle");
    imshow("circle", dst1);
    cv::waitKey(0);
    }

实验效果：

从实验效果图中可以看出，circle LBP的纹理特征提取的更加明显。

基本LBP算法实现:比较简单

void LBP(Mat& src, Mat& dst)
{
       int width = src.cols;
       int height = src.rows;
       for (int i = 1; i <= height - 1; ++i)
       {
              for (int j = 1; j <= width - 1; ++j)
              {
                 uchar neighbor[8] = { 0 };
                     neighbor[7] = src.at(i-1, j-1);
                     neighbor[6] = src.at(i-1,j);
                     neighbor[5] = src.at(i - 1, j + 1);
                     neighbor[4] = src.at(i, j + 1);
                     neighbor[3] = src.at(i + 1, j + 1);
                     neighbor[2] = src.at(i + 1, j);
                     neighbor[1] = src.at(i + 1, j - 1);
                     neighbor[0] = src.at(i, j - 1);
                     uchar curr = src.at(i, j);
                     uchar temp = 0;
                     for (int k = 0; k < 8; k++)
                     {
                            temp +=  (neighbor[k] >= curr)<< k;
                     }
                     dst.at(i-1, j-1) = temp;
              }
       }
}

5、LBP算法在人脸识别中的应用

    今天先学习到这里，下次继续更新LBP局部二值模式在纹理提取和人脸识别中的具体应用。