学习笔记8：常用损失函数之交叉熵（Cross Entropy）

1.信息量

假设X是一个离散型随机变量，其取值集合为 X X ，概率分布函数为 p(x)=Pr(X=x),x∈X p ( x ) = P r ( X = x ) , x ∈ X ，我们定义事件 X=x0 X = x 0 的信息量为： I(x0)=−log(p(x0)) I ( x 0 ) = − l o g ( p ( x 0 ) ) 可以理解为，一个事件发生的概率越大，则它所携带的信息量就越小，而当p(x0)=1时，熵将等于0，也就是说该事件的发生不会导致任何信息量的增加。

2.熵的概念

对于一个随机变量X而言，它的所有可能取值的信息量的期望E[I(x)]就称为熵。
X的熵的定义为：

H(X)=Eplog1p(x)=−∑x∈Xp(x)logp(x) H ( X ) = E p log ⁡ 1 p ( x ) = − ∑ x ∈ X p ( x ) log ⁡ p ( x )

如果p(x)是连续型随机变量的pdf，则熵定义为：

H(X)=−∫x∈Xp(x)logp(x)dx H ( X ) = − ∫ x ∈ X p ( x ) log ⁡ p ( x ) d x

为了保证有效性，这里约定当p(x)→0时,有 p(x)→0时,有p(x)logp(x)→0 p ( x ) → 0 时 , 有 p ( x ) log ⁡ p ( x ) → 0

当X为0-1分布时，熵与概率p的关系如下图：

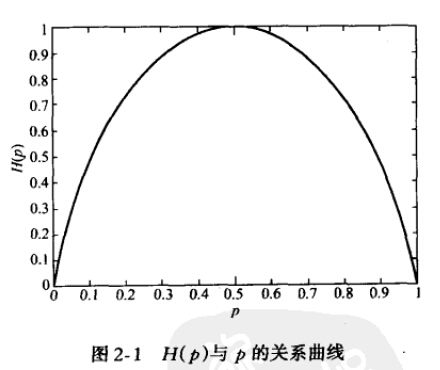
可以看出，当两种取值的可能性相等时，不确定度最大（此时没有任何先验知识），这个结论可以推广到多种取值的情况。在图中也可以看出，当p=0或1时，熵为0，即此时X完全确定。
熵的单位随着公式中log运算的底数而变化，当底数为2时，单位为“比特”(bit)，底数为e时，单位为“奈特”。

3.相对熵

相对熵(relative entropy)又称为KL散度（Kullback-Leibler divergence），KL距离，是两个随机分布间距离的度量。记为 DKL(p||q) D K L ( p | | q ) 。它度量当真实分布为p时，假设分布q的无效性。

DKL(p||q)=Ep[logp(x)q(x)]=∑x∈Xp(x)logp(x)q(x) D K L ( p | | q ) = E p [ log ⁡ p ( x ) q ( x ) ] = ∑ x ∈ X p ( x ) log ⁡ p ( x ) q ( x )

=∑x∈X[p(x)logp(x)−p(x)logq(x)] = ∑ x ∈ X [ p ( x ) log ⁡ p ( x ) − p ( x ) log ⁡ q ( x ) ]

=∑x∈Xp(x)logp(x)−∑x∈Xp(x)logq(x) = ∑ x ∈ X p ( x ) log ⁡ p ( x ) − ∑ x ∈ X p ( x ) log ⁡ q ( x )

=−H(p)−∑x∈Xp(x)logq(x) = − H ( p ) − ∑ x ∈ X p ( x ) log ⁡ q ( x )

=−H(p)+Ep[−logq(x)] = − H ( p ) + E p [ − log ⁡ q ( x ) ]

=Hp(q)−H(p) = H p ( q ) − H ( p )

显然，当p=q时,两者之间的相对熵 DKL(p||q)=0 D K L ( p | | q ) = 0

4.交叉熵

交叉熵容易跟相对熵搞混，二者联系紧密，但又有所区别。假设有两个分布p，q，则它们在给定样本集上的交叉熵定义如下：

CEH(p,q)=Ep[−logq]=−∑x∈Xp(x)logq(x)=H(p)+DKL(p||q) C E H ( p , q ) = E p [ − log ⁡ q ] = − ∑ x ∈ X p ( x ) log ⁡ q ( x ) = H ( p ) + D K L ( p | | q )

举例来讲，对于一个二分类问题，我们可以将真实概率表达为 p∈{y,1−y}，并且将预测概率表达为 q∈{y^,1−y^} q ∈ { y ^ , 1 − y ^ } 。这样的话，我们可以通过交叉熵来测量 p 和 q 之间的相似度：

H(p,q)=−∑ipilogqi=−ylogy^−(1−y)log(1−y^) H ( p , q ) = − ∑ i p i log ⁡ q i = − y log ⁡ y ^ − ( 1 − y ) log ⁡ ( 1 − y ^ )

参考：https://blog.csdn.net/rtygbwwwerr/article/details/50778098
https://www.zhihu.com/question/41252833